Kombinované namáhání

Načtení nutných knihoven

In [2]:
%matplotlib inline
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

a inicializace sázeného výstupu,

In [3]:
sp.init_printing()

Př1:

U rámu podle obrázku posuďte bezpečnost vzhledem k meznímu stavu pružnosti, příp. vzpěrné stability, jestliže je dáno,

$\sigma_k=350\,\mathrm{MPa}$

$F=10\,\mathrm{kN}$

$E=2.1\times10^5\,\mathrm{MPa}$

$R=350\,\mathrm{mm}$, $h=50\,\mathrm{mm}$, $b=15\,\mathrm{mm}$

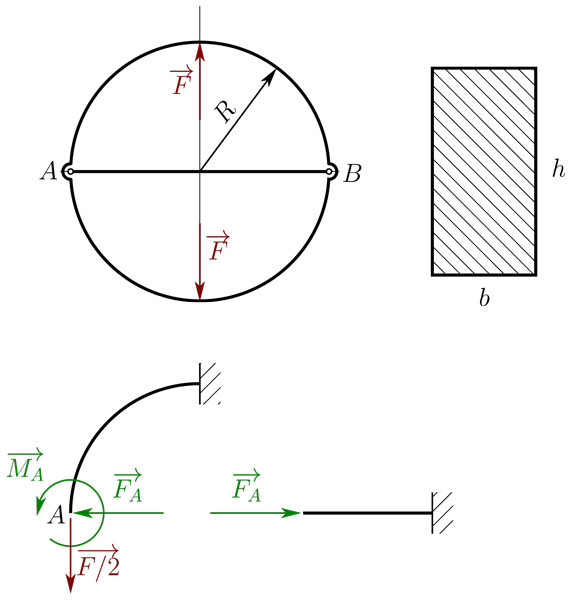
Obrázek

Úloha je $2\times$ staticky neurčitá.

Úkol: Proveďte úplné uvolnění a statický rozbor.

Částečné uvolnění lze provést několika způsoby, jedno z nich využívající symetrii úlohy ukazuje výše uvedený obrázek, který je nutné doplnit deformačními podmínkami,

\begin{eqnarray} && w_A^I=u_A^{II}\quad\Rightarrow\quad\frac{\partial W^I}{\partial F_{A}}=-\frac{\partial W^{II}}{\partial F_{A}}, \\ && \varphi_A^I=0\quad\Rightarrow\quad\frac{\partial W^I}{\partial M_{A}}=0, \end{eqnarray}

kde horní index $I$ odpovídá zakřivenému prutu, horní index $II$ odpovídá přímému prutu.

Zavedení potřebných symbolů,

In [4]:
T,N,M=sp.Function('T'),sp.Function('N'),sp.Function('M')
s,theta=sp.symbols('s theta',real=True)
l=sp.symbols('s')
R=sp.symbols('R',real=True,positive=True)
p,q=sp.symbols('p q')
E,J,S=sp.symbols('E J S')
C_1,C_2,D_1,D_2=sp.symbols('C_1 C_2 D_1 D_2',complex=True)
C_3=sp.symbols('C_3',real=True)
F_A,F,M_A=sp.symbols('F_A F M_A',real=True)

Poznámka: Vnitřní účinky jsou zde řešeny diferencálním způsobem v křivočarých souřadnicích. Je to určitě zajímavé, avšak doporučuji si je vyjádřit klasicky integrálním způsobem pěkně růčo a zkontrolovat s výsledky uvedenými zde.

Úkol: Vyjádřete výsledné vnitřní účinky integrálním způsobem.

Soustava diferenciální rovnice vnitřních účinků v křivočarých (polárních) souřadnicích,

\begin{eqnarray} \frac{\mathrm{d}T(s)}{\mathrm{d}s}+\frac{N(s)}{R}&=&-q(s), \\ \frac{\mathrm{d}N(s)}{\mathrm{d}s}&=&\frac{T(s)}{R}, \\ \frac{\mathrm{d}M(s)}{\mathrm{d}s}&=&T(s), \end{eqnarray}

kde $s$ je délka oblouku měřená ve směru hodinových ručiček (nemusí být nutně kruhový), $R$ je jeho poloměr a $q(s)$ je liniové zatížení podél oblouku $s$.

Výše uvedená soustava diferenciálích rovnic zapsaná v Pythonu pro konstantní $q$,

In [5]:
deqn1=T(s).diff(s)+q+N(s)/R
deqn2=N(s).diff(s)-T(s)/R
deqn3=M(s).diff(s)-T(s)
deqn1,deqn2,deqn3
Out[5]:
$$\left ( q + \frac{d}{d s} T{\left (s \right )} + \frac{1}{R} N{\left (s \right )}, \quad \frac{d}{d s} N{\left (s \right )} - \frac{1}{R} T{\left (s \right )}, \quad - T{\left (s \right )} + \frac{d}{d s} M{\left (s \right )}\right )$$

Derivováním druhé rovnice podle $s$ a její dosazení do rovnice první se dostane obyčejná diferenciální rovnice druhého řádu pro normálovou složku $N(s)$,

\begin{equation} R\frac{\mathrm{d}^2N(s)}{\mathrm{d}s^2}+\frac{N(s)}{R}=-q(s). \end{equation}

V Pythonu se to může provést následovně,

In [6]:
deqn2s=deqn2.diff(s)
deqn2s
Out[6]:
$$\frac{d^{2}}{d s^{2}} N{\left (s \right )} - \frac{1}{R} \frac{d}{d s} T{\left (s \right )}$$
In [7]:
sol1=sp.solve(deqn2s,T(s).diff(s))
sol1
Out[7]:
$$\left [ R \frac{d^{2}}{d s^{2}} N{\left (s \right )}\right ]$$
In [8]:
deqn10=deqn1.subs(T(s).diff(s),sol1[0])
deqn10
Out[8]:
$$R \frac{d^{2}}{d s^{2}} N{\left (s \right )} + q + \frac{1}{R} N{\left (s \right )}$$

Jde o lineární diferenciání rovnici druhého řádu. Za předpokladu, že $q=0$ se řešení předchozí rovnice předpokládá ve tvaru

\begin{equation} N(s)=\mathrm{e}^{ps}, \end{equation}

kde $p$ je obecně komplexní číslo. Dosazení $N(s)=\mathrm{e}^{ps}$ do výše uvedené diferenciální rovnice se v Pythonu provede následovně,

In [9]:
deqn11=deqn10.subs({N(s):sp.exp(p*s),q:0})
deqn11
Out[9]:
$$R \frac{\partial^{2}}{\partial s^{2}} e^{p s} + \frac{e^{p s}}{R}$$
In [10]:
deqn12=deqn11.doit()
deqn12
Out[10]:
$$R p^{2} e^{p s} + \frac{e^{p s}}{R}$$

Po úpravách se dostane tzv. charakteristická rovnice, ze které se vyjádří $p$.

In [11]:
eqn3=sp.collect(deqn12,sp.exp(p*s),evaluate=False)
eqn4=eqn3[sp.exp(p*s)]
eqn4
Out[11]:
$$R p^{2} + \frac{1}{R}$$

Řešení této kvadratické rovnice vzhledem k neznámé $p$ je,

In [12]:
sol3=sp.solve(eqn4,p)
sol3
Out[12]:
$$\left [ - \frac{i}{R}, \quad \frac{i}{R}\right ]$$

Protože platí vztah,

\begin{equation} \mathrm{e}^{is}=\cos\left(s\right)+i\sin\left(s\right) \end{equation}

může se řešení $N(s)$ případě ryze komplexního parametru $p=\pm i\left|p\right|$ psát v následujícím tvaru,

\begin{equation} N\left(\theta\right)=C_1\left[\cos(\theta)+i\sin\left(\theta\right)\right]+C_2\left[\cos\left(\theta\right)-i\sin\left(\theta\right)\right] \end{equation}

kde

\begin{equation} \theta=\frac{s}{R} \end{equation}

je úhel, který svírá bod $s$ s vodorovnou osou měřený ve smyslu hodinových ručiček,

In [13]:
N0=C_1*sp.expand_complex(sp.exp(sol3[0]*s))+C_2*sp.expand_complex(sp.exp(sol3[1]*s))
N0
Out[13]:
$$C_{1} \left(- i \sin{\left (\frac{s}{R} \right )} + \cos{\left (\frac{s}{R} \right )}\right) + C_{2} \left(i \sin{\left (\frac{s}{R} \right )} + \cos{\left (\frac{s}{R} \right )}\right)$$

Předchozí rovnici lze získat přímo pomocí příkazu dsolve (viz. pruhybová čára).

Úkol: Vygenerujte vztah pro $N\left(s\right)$ pomocí příkazu dsolve.

Neznámé konstanty $C_1$ a $C_2$ jsou obecně komplexní a určí se z okrajových podmínek, které pro $s=R\theta$ mají tvar,

\begin{eqnarray} N(s)&=&\frac{F}{2}\quad\mathrm{pro}\quad s=0,\\ N(s)&=&F_A\quad\mathrm{pro}\quad s=R\frac{\pi}{2}. \end{eqnarray}

Výše napsané okrajové podmínky se v Pythonu mohou zapsat následovně,

In [14]:
bc=[sp.re(N0.subs(s,0))-F/2,sp.im(N0.subs(s,0)),sp.re(N0.subs(s,R*sp.pi/2)-F_A),sp.im(N0.subs(s,R*sp.pi/2)-F_A)]
bc
Out[14]:
$$\left [ - \frac{F}{2} + \Re{C_{1}} + \Re{C_{2}}, \quad \Im{C_{1}} + \Im{C_{2}}, \quad - F_{A} + \Im{C_{1}} - \Im{C_{2}}, \quad - \Re{C_{1}} + \Re{C_{2}}\right ]$$

Poznámka: Je nutné si uvědomit, že knihovna Sympy předpokládá, že se vždy každá rovnice automaticky rovná nule. Je to geniální syntaktická zkratka, která nemá potřebu zavádět spěciální znaky pro rovnost v rovnicích a pro přiřazení proměnné, jak je tomu u jiných CAS systémů. Z tohoto důvodu se v předchozím výrazu (listu-seznamu) nevysytuje zádné rovnítko a "rovno nule" se jednoduše vynechává. Symboly $\Re$ a $\Im$ značí reálnou a imaginární část neznámých konstant $C_1$ a $C_2$.

Řešení předchozí soutavy algebraických rovnic sestavených z okrajových podmínek je,

In [15]:
sol4=sp.solve(bc,[sp.re(C_1),sp.re(C_2),sp.im(C_1),sp.im(C_2)])
sol4
Out[15]:
$$\left \{ \Re{C_{1}} : \frac{F}{4}, \quad \Re{C_{2}} : \frac{F}{4}, \quad \Im{C_{1}} : \frac{F_{A}}{2}, \quad \Im{C_{2}} : - \frac{F_{A}}{2}\right \}$$

a jeho dosazením do $N(s)$ se dostane jeho výsledné řešení,

In [16]:
N1=N0.subs(C_1,sol4[sp.re(C_1)]+sp.I*sol4[sp.im(C_1)])
N2=N1.subs(C_2,sol4[sp.re(C_2)]+sp.I*sol4[sp.im(C_2)])
N=N2.simplify()
N
Out[16]:
$$\frac{F}{2} \cos{\left (\frac{s}{R} \right )} + F_{A} \sin{\left (\frac{s}{R} \right )}$$

Výsledné řešení pro $T(s)$ se dostane na základě vztahu,

$$ T\left(s\right)=R\frac{\mathrm{d}N\left(s\right)}{\mathrm{d}s}, $$
In [17]:
T1=R*N.diff(s)
T=T1.simplify()
T
Out[17]:
$$- \frac{F}{2} \sin{\left (\frac{s}{R} \right )} + F_{A} \cos{\left (\frac{s}{R} \right )}$$

Pro moment platí $M(s)$

$$ M\left(s\right)=\int T\left(s\right)\mathrm{d}s+C_3, $$

kde se integrační konstanta $C_3$ vyjádří z okrajové podmínky,

\begin{equation} M(s)=-M_A.\quad\mathrm{pro}\quad s=0. \end{equation}

Toto se v Pythonu provede následovně,

In [18]:
M1=sp.integrate(T,s)+C_3
M1
Out[18]:
$$C_{3} + \frac{F R}{2} \cos{\left (\frac{s}{R} \right )} + F_{A} R \sin{\left (\frac{s}{R} \right )}$$
In [19]:
bc=M1.subs(s,0)+M_A
bc
Out[19]:
$$C_{3} + \frac{F R}{2} + M_{A}$$
In [20]:
sol5=sp.solve(bc,C_3)
sol5
Out[20]:
$$\left [ - \frac{F R}{2} - M_{A}\right ]$$

Výsledné řešení pro $M(s)$ má ve finále tvar,

In [21]:
M=M1.subs(C_3,sol5[0])
M
Out[21]:
$$\frac{F R}{2} \cos{\left (\frac{s}{R} \right )} - \frac{F R}{2} + F_{A} R \sin{\left (\frac{s}{R} \right )} - M_{A}$$

Celkem všechny vnitřní výsledné účinky zakřiveného prutu v závislosti na úhlu $\theta$, kde $s=R\theta$,

In [22]:
Nt=N.subs(s,R*theta)
Tt=T.subs(s,R*theta)
Mt=M.subs(s,R*theta)
Nt,Tt,Mt
Out[22]:
$$\left ( \frac{F}{2} \cos{\left (\theta \right )} + F_{A} \sin{\left (\theta \right )}, \quad - \frac{F}{2} \sin{\left (\theta \right )} + F_{A} \cos{\left (\theta \right )}, \quad \frac{F R}{2} \cos{\left (\theta \right )} - \frac{F R}{2} + F_{A} R \sin{\left (\theta \right )} - M_{A}\right )$$

Vnitřní výsledné účinky přímého prutu,

In [23]:
N2=F_A
N2
Out[23]:
$$F_{A}$$

Odstranění statické neurčitosti vyřešením deformačních podmínek,

\begin{equation} \varphi_A^I=\frac{\partial W^I}{\partial M_A}=\int_0^{\pi/2}\frac{M^I(\theta)}{EJ}\frac{\partial M^I(\theta)}{\partial M_A}R\mathrm{d}\theta=0 \end{equation}

a

\begin{equation} w_A^I=\frac{\partial W^I}{\partial F_A}=\int_0^{\pi/2}\frac{M^I(\theta)}{EJ}\frac{\partial M^I(\theta)}{\partial F_A}R\mathrm{d}\theta=-\frac{2N^{II}R}{ES}\frac{\partial N^{II}}{\partial F_A}=-\frac{\partial W^{II}}{\partial F_A}=u_A^{II}. \end{equation}

Derivace $M^I$ podle $M_A$ a $F_A$,

In [24]:
dMtdM_A=Mt.diff(M_A)
dMtdF_A=Mt.diff(F_A)
dMtdM_A,dMtdF_A
Out[24]:
$$\left ( -1, \quad R \sin{\left (\theta \right )}\right )$$

Rovnice deformačních podmínek pro neznámé $F_A$ a $M_A$,

In [25]:
eqn1=sp.integrate(Mt/E/J*dMtdM_A*R,(theta,0,sp.pi/2))
eqn2=sp.integrate(Mt/E/J*dMtdF_A*R,(theta,0,sp.pi/2))+2*F_A/E/S*R
eqn1,eqn2
Out[25]:
$$\left ( - \frac{F_{A} R^{2}}{E J} - \frac{R}{E J} \left(- \frac{\pi F}{4} R + \frac{F R}{2} - \frac{\pi M_{A}}{2}\right), \quad \frac{2 F_{A} R}{E S} + \frac{\pi F_{A} R^{3}}{4 E J} - \frac{R^{2}}{E J} \left(\frac{F R}{4} + M_{A}\right)\right )$$

a jejich řešení,

In [26]:
eqn1_=sp.collect(sp.expand(eqn1),[F_A,M_A])
eqn2_=sp.collect(sp.expand(eqn2),[F_A,M_A])
sol6=sp.linsolve([eqn1_,eqn2_],[F_A,M_A])
F_A_,M_A_=next(iter(sol6))
F_A_,M_A_
Out[26]:
$$\left ( \frac{F R^{2} S \left(- \pi + 4\right)}{8 \pi J - 8 R^{2} S + \pi^{2} R^{2} S}, \quad - \frac{F R \left(4 R^{2} S + \left(- \pi + 2\right) \left(8 J + \pi R^{2} S\right)\right)}{16 R^{2} S - 2 \pi \left(8 J + \pi R^{2} S\right)}\right )$$

Namáhání prutů se vyšetří na konkrétním zadání. Zadané hodnoty jsou v [mm], [N] a [MPa],

In [27]:
b_,h_=15.0,50.0
J_=1/12.0*b_*h_**3
S_=b_*h_
F_=10000.0
r_=350
E_=2.1e5
sigma_k_=350

Velikost a smysl síly $F_A$ a momentu $M_A$,

In [28]:
F_A_ev=float(F_A_.subs({R:r_,S:S_,J:J_,F:F_}))
F_A_ev
Out[28]:
$$4488.76315523$$
In [29]:
M_A_ev=float(M_A_.subs({R:r_,S:S_,J:J_,F:F_}))
M_A_ev
Out[29]:
$$364256.983976$$

Vyjádření normálové složky $N\left(\theta\right)$ vnitřních účinků zakřiveného prutu,

In [30]:
Ntf=Nt.subs({M_A:M_A_ev,F_A:F_A_ev,F:F_})
Ntf
Out[30]:
$$4488.76315523066 \sin{\left (\theta \right )} + 5000.0 \cos{\left (\theta \right )}$$

Vyjádření $T\left(\theta\right)$ vnitřních účinků zakřiveného prutu,

In [31]:
Ttf=Tt.subs({M_A:M_A_ev,F_A:F_A_ev,F:F_})
Ttf
Out[31]:
$$- 5000.0 \sin{\left (\theta \right )} + 4488.76315523066 \cos{\left (\theta \right )}$$

Vyjádření $M\left(\theta\right)$ vnitřních účinků zakřiveného prutu,

In [32]:
Mtf=Mt.subs({M_A:M_A_ev,F_A:F_A_ev,F:F_,R:r_})
Mtf
Out[32]:
$$1571067.10433073 \sin{\left (\theta \right )} + 1750000.0 \cos{\left (\theta \right )} - 2114256.98397649$$

Pro vykreslení vnitřních účinků se tyto vyjádří v bodech rovnoměrně rozložených podél střednice,

In [33]:
bodu=20
meritko=5.

thetaI=np.linspace(0,np.pi/2,bodu)

strednice_x=[-np.cos(ii) for ii in thetaI]
strednice_y=[np.sin(ii) for ii in thetaI]

grid_x=[[0,0],[0,-(1+1/(meritko-1))*np.cos(np.pi/4.)],[0,(-1-1/(meritko-1))]]
grid_y=[[0,(1+1/(meritko-1))],[0,(1+1/(meritko-1))*np.sin(np.pi/4.)],[0,0]]

N_plot=[float(Ntf.subs(theta,ii)) for ii in thetaI]
N_plot_max=abs(max(N_plot))
N_plot_x=[(N_plot[ii]/meritko/N_plot_max+1)*strednice_x[ii] for ii in range(bodu)]
N_plot_y=[(N_plot[ii]/meritko/N_plot_max+1)*strednice_y[ii] for ii in range(bodu)]

T_plot=[float(Ttf.subs(theta,ii)) for ii in thetaI]
T_plot_max=abs(max(T_plot))
T_plot_x=[(T_plot[ii]/meritko/T_plot_max+1)*strednice_x[ii] for ii in range(bodu)]
T_plot_y=[(T_plot[ii]/meritko/T_plot_max+1)*strednice_y[ii] for ii in range(bodu)]

M_plot=[float(Mtf.subs(theta,ii)) for ii in thetaI]
M_plot_max=abs(max(M_plot))
M_plot_x=[(M_plot[ii]/meritko/M_plot_max+1)*strednice_x[ii] for ii in range(bodu)]
M_plot_y=[(M_plot[ii]/meritko/M_plot_max+1)*strednice_y[ii] for ii in range(bodu)]

Vykreslení normálové složky $N\left(\theta\right)$ podél střednice zakřiveného prutu,

In [34]:
fig,ax=plt.subplots()
ax.axis("equal")
ax.tick_params(
    which='both',      # both major and minor ticks are affected
    bottom='off',      # ticks along the bottom edge are off
    top='off',         # ticks along the top edge are off
    labelbottom='off',
    left='off',
    right='off',
    labelleft='off') # labels along the bottom edge are off
ax.set_ylim(-0.05,1.3)
ax.set_title('Normalova slozka $N$ '+r'$[\mathrm{N}]$')
ax.plot(N_plot_x,N_plot_y,color="red",label='N',lw=2)
for ii in grid_x:
  ax.plot(ii,grid_y[grid_x.index(ii)],color="grey",lw=0.5)
for ii in range(bodu):
  pointx=[strednice_x[ii],N_plot_x[ii]]
  pointy=[strednice_y[ii],N_plot_y[ii]]
  ax.plot(pointx,pointy,color="red",lw=1)
  ax.text(pointx[1],pointy[1],str(int(N_plot[ii])), \
          horizontalalignment="left",fontsize=8,color="grey", \
          rotation=(-180.*thetaI[ii]/np.pi))
ax.plot(strednice_x,strednice_y,color="blue",label="strednice",lw=3)
ax.legend(loc='upper left')
Out[34]:
<matplotlib.legend.Legend at 0x7fec130217d0>

Vykreslení posouvající složky $T\left(\theta\right)$ podél střednice zakřiveného prutu,

In [35]:
fig,ax=plt.subplots()
ax.axis("equal")
ax.tick_params(
    which='both',      # both major and minor ticks are affected
    bottom='off',      # ticks along the bottom edge are off
    top='off',         # ticks along the top edge are off
    labelbottom='off',
    left='off',
    right='off',
    labelleft='off') # labels along the bottom edge are off
ax.set_ylim(-0.05,1.3)
ax.set_title('Posouvajici slozka $T$ '+r"[$\mathrm{N}$]")
ax.plot(T_plot_x,T_plot_y,color="red",label='T',lw=2)
for ii in grid_x:
  ax.plot(ii,grid_y[grid_x.index(ii)],color="grey",lw=0.5)
for ii in range(bodu):
  pointx=[strednice_x[ii],T_plot_x[ii]]
  pointy=[strednice_y[ii],T_plot_y[ii]]
  ax.plot(pointx,pointy,color="red",lw=1)
  ax.text(pointx[1],pointy[1],str(int(T_plot[ii])), \
          horizontalalignment="left",fontsize=8,color="grey", \
          rotation=(-180.*thetaI[ii]/np.pi))
ax.plot(strednice_x,strednice_y,color="blue",label="strednice",lw=3)
ax.legend(loc='upper left')
Out[35]:
<matplotlib.legend.Legend at 0x7fec153ecf90>

Vykreslení momentové složky $M\left(\theta\right)$ podél střednice zakřiveného prutu,

In [36]:
fig,ax=plt.subplots()
ax.axis("equal")
ax.tick_params(
    which='both',      # both major and minor ticks are affected
    bottom='off',      # ticks along the bottom edge are off
    top='off',         # ticks along the top edge are off
    labelbottom='off',
    left='off',
    right='off',
    labelleft='off') # labels along the bottom edge are off
ax.set_ylim(-0.05,1.3)
ax.set_title('Momentova slozka $M$ '+r'$[\mathrm{N}\times\mathrm{mm}]$')
ax.plot(M_plot_x,M_plot_y,color="red",label='M',lw=2)
for ii in grid_x:
  ax.plot(ii,grid_y[grid_x.index(ii)],color="grey",lw=0.5)
for ii in range(bodu):
  pointx=[strednice_x[ii],M_plot_x[ii]]
  pointy=[strednice_y[ii],M_plot_y[ii]]
  ax.plot(pointx,pointy,color="red",lw=1)
  ax.text(pointx[1],pointy[1],str(int(M_plot[ii])), \
          horizontalalignment="left",fontsize=8,color="grey", \
          rotation=(-180.*thetaI[ii]/np.pi))
ax.plot(strednice_x,strednice_y,color="blue",label="strednice",lw=3)
ax.legend(loc='upper left')
Out[36]:
<matplotlib.legend.Legend at 0x7fec12eb3610>

Kontrola k meznímu stavu pružnosti zakřiveného rámu

Z grafu pro $M(\theta)$ je patrné, že nebezpečný průřez je v místě působení síly $F$, tedy pro $\theta=\pi/2$. Dochází zde však ke kombinaci napětí. Proto v příčném průřezu nejdříve vyjáříme průběhy napětí podle vztahů,

\begin{eqnarray} &&\sigma_x=\frac{N}{S}, \\ &&\tau_{xz}=\frac{6T}{bh^3}\left(\frac{h^2}{4}-z^2\right)\quad\Leftarrow\quad\mathrm{tzv.}\,\mathrm{Žuravského}\,\mathrm{vztah}, \\ &&\sigma_x=\frac{M}{J_y}z. \end{eqnarray}

Vykreslení rozložení normálového napětí $\sigma_x^N\left(y,z\right)$ od složky $N\left(\theta\right)$ v příčném průřezu (šedý obdélník odpovídá nulovým hodnotám napětí $\sigma_x^N\left(y,z\right)$),

In [38]:
x,y,z=[],[],[]
for ii in np.linspace(-7.5,7.5,15): 
  for jj in np.linspace(-25,25,50):
    x.append(ii)
    y.append(jj)
    z.append(float(Ntf.subs(theta,np.pi/2.))/b_/h_)
In [39]:
fig = plt.figure(figsize=(10,10))
ax = fig.gca(projection='3d')
ax.set_xlim3d(-35,35)
ax.set_ylim3d(-35,35)
#ax.set_zlim3d(-150,150)
ax.set_xlabel('$y$'+' '+r'$[\mathrm{mm}]$').set_fontsize(18)
ax.set_ylabel('$z$'+' '+r'$[\mathrm{mm}]$').set_fontsize(18)
ax.set_zlabel('$\sigma^N_x$'+' '+r'$[\mathrm{MPa}]$').set_fontsize(18)
ax.set_title('Normalove napeti $\sigma_x$\n od normalovych vnitrnich ucinku '+r'$N$' \
             +'\nv pricnem prurezu '+r'$\theta=\frac{\pi}{2}$').set_fontsize(18)
ax.plot([-b_/2,-b_/2,b_/2,b_/2,-b_/2],[-h_/2,h_/2,h_/2,-h_/2,-h_/2],color='grey')
ax.plot_trisurf(x, y, z, cmap=cm.jet, linewidth=0.2)
Out[39]:
<mpl_toolkits.mplot3d.art3d.Poly3DCollection at 0x7fec1270f510>

Vykreslení rozložení smykového napětí $\tau_{xz}^T\left(y,z\right)$ od posouvající síly v příčném průřezu (šedý obdélník odpovídá nulovým hodnotám napětí $\tau_{xz}^T\left(y,z\right)$),

In [40]:
x,y,z=[],[],[]
for ii in np.linspace(-7.5,7.5,15): 
  for jj in np.linspace(-25,25,50):
    x.append(ii)
    y.append(jj)
    z.append(6*float(Ttf.subs(theta,np.pi/2.))/b_/h_**3*(h_**2/4-jj**2)) #tzv. Zuravskeho vzorec pro obdelnik
In [41]:
fig = plt.figure(figsize=(10,10))
ax = fig.gca(projection='3d')
ax.set_xlim3d(-35,35)
ax.set_ylim3d(-35,35)
ax.set_zlim3d(-20,10)
ax.set_xlabel('$y$'+' '+r'$[\mathrm{mm}]$').set_fontsize(18)
ax.set_ylabel('$z$'+' '+r'$[\mathrm{mm}]$').set_fontsize(18)
ax.set_zlabel(r'$\tau^T_{xz}$'+' '+r'$[\mathrm{MPa}]$').set_fontsize(18)
ax.set_title('Smykove napeti '+r'$\tau_{xz}$'+'\n od posouvajicich vnitrnich ucinku '+r'$T_z$' \
             +'\nv pricnem prurezu '+r'$\theta=\frac{\pi}{ 2}$').set_fontsize(18)
ax.plot([-b_/2,-b_/2,b_/2,b_/2,-b_/2],[-h_/2,h_/2,h_/2,-h_/2,-h_/2],color='grey')
ax.plot_trisurf(x, y, z, cmap=cm.jet, linewidth=0.2)
Out[41]:
<mpl_toolkits.mplot3d.art3d.Poly3DCollection at 0x7fec122897d0>

Vykreslení rozložení normálového napětí $\sigma_x^M\left(y,z\right)$ od momentové složky $M\left(\theta\right)$ výsledných vnitřních účinků v příčném průřezu (šedý obdélník odpovídá nulovým hodnotám napětí $\sigma_x^M\left(y,z\right)$),

In [42]:
x,y,z=[],[],[]
for ii in np.linspace(-7.5,7.5,15): 
  for jj in np.linspace(-25,25,50):
    x.append(ii)
    y.append(jj)
    z.append(-float(Mtf.subs(theta,np.pi/2.))/J_*jj) #z duvodu lepsiho zobrazeni je u momentu znamenko minus
In [48]:
fig = plt.figure(figsize=(10,10))
ax = fig.gca(projection='3d')
ax.set_xlim3d(-35,35)
ax.set_ylim3d(-35,35)
ax.set_zlim3d(-150,150)
ax.set_xlabel('$y$'+' '+r'$[\mathrm{mm}]$').set_fontsize(18)
ax.set_ylabel('$z$'+' '+r'$[\mathrm{mm}]$').set_fontsize(18)
ax.set_zlabel('$\sigma^M_x$'+' '+r'$[\mathrm{MPa}]$').set_fontsize(18)
ax.set_title('Normalove napeti $\sigma_x$\n od momentovych vnitrnich ucinku '+r'$M_y$' \
             +'\nv pricnem prurezu '+r'$\theta=\frac{\pi}{ 2}$').set_fontsize(18)
ax.plot([-b_/2,-b_/2,b_/2],[-h_/2,h_/2,h_/2],color='grey')
ax.plot_trisurf(x, y, z, cmap=cm.jet, linewidth=0.2)
ax.plot([-b_/2,b_/2,b_/2],[-h_/2,-h_/2,h_/2],color='grey')
Out[48]:
[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7fec0bfb39d0>]

V krajních vláknech příčného průřezu, tj. pro $z=-\frac{h}{2}$, je normálové napětí superozicí napětí od výsledných vnitřních účinků $N$ a $M$,

\begin{equation} \sigma_{x,max}=\frac{\left|N\left(\frac{\pi}{2}\right)\right|}{S}+\frac{\left|M\left(\frac{\pi}{2}\right)\right|}{W_o}, \end{equation}

kde

\begin{equation} S=bh\quad a\quad W_o=\frac{1}{6}bh^2. \end{equation}

Maximální hodnota napětí $\sigma_x$ v příčném průřezu má hodnotu,

In [50]:
sigma_max=float(abs(Ntf.subs(theta,np.pi/2.)))/(b_*h_)+float(abs(Mtf.subs(theta,np.pi/2.)))*6/b_/h_**2
sigma_max
Out[50]:
$$92.8953982836$$

Na střednici prutu studovaného příčného průřezu, tj. pro $z=0$, je superozice normálového napětí od složky vnitřních účinků $N$ a smykového napětí od složky vnitřních účinků $T$. Redukované napětí se vyjádří podle Trescovy teorie,

\begin{equation} \sigma_{red}=\sqrt{\left(\sigma^N_x\right)^2+4\left(\tau^T_{xz}\right)^2}=\sqrt{\left(\frac{N\left(\frac{\pi}{2}\right)}{S}\right)^2+4\left(\frac{3T\left(\frac{\pi}{2}\right)}{2S}\right)^2}. \end{equation}

Redukované napětí $\sigma_{red}$ má velikost,

In [52]:
sigma_red=np.sqrt((float(Ntf.subs(theta,np.pi/2.))/b_/h_)**2+4*(3*float(Ttf.subs(theta,np.pi/2.))/2/b_/h_)**2)
sigma_red
Out[52]:
$$20.8763127721$$

Bezpečnost vzhledem k meznímu stavu pružosti zakřiveného prutu,

\begin{equation} k=\mathrm{min}\left\{ \frac{\sigma_k}{\sigma_{max}},\frac{\sigma_k}{\sigma_{red}}\right\}. \end{equation}
In [54]:
k1=min([sigma_k_/sigma_max,sigma_k_/sigma_red])
k1
Out[54]:
$$3.76767855531$$

Kontrola k meznímu stavu vzpěrné stability přímého prutu

Vzhledem k tomu, že daný příčný průřez bez problémů snese kombinaci tahového a smykového napětí v případě zakřiveného prutu namáhaného ohybem, nemá smysl kontorolovat stejný příčný průřez na jeho schopnost snést prostý tah a tlak. Proto přímý prut namáhaný tlakem by stačilo kontrolovat jen vzhledem k míře jeho schopnosti odolat svému borcení. Přesto se dále budeme držet metodiky a rozhodnutí o správném způsobu kontroly necháme na ní. K tomu je nutné si zavést následující geometrické charakteristiky a posoudit způsob uložení konců prutu,

Geometrické charakteristiky,

\begin{eqnarray} &&J_{min}=\frac{1}{12}b^3h, \\ &&i=\sqrt{\frac{J_{min}}{S}}, \\ &&\lambda=\frac{R}{i} \end{eqnarray}

a charakter uložení (jeden konec prutu je volný, druhý je vetknutý),

\begin{equation} \alpha=\frac{\pi}{2}. \end{equation}

Konkrétně a Pythonovsky,

In [55]:
J_min=1./12.*b_**3*h_
i=np.sqrt(J_min/b_/h_)
lambda_=r_/i
alpha=np.pi/2
J_min,i,lambda_,alpha
Out[55]:
$$\left ( 14062.5, \quad 4.33012701892, \quad 80.8290376865, \quad 1.57079632679\right )$$

Mezní štíhlost,

\begin{equation} \lambda_k=\sqrt{\frac{\alpha^2E}{\sigma_k}}. \end{equation}
In [57]:
lambda_k=np.sqrt(alpha**2*E_/sigma_k_)
lambda_k
Out[57]:
$$38.4764949049$$

Bezpečnost přímého prutu se stanoví podle relace mezi $\lambda$ a $\lambda_k$,

  • $\lambda<\lambda_k$ $\Rightarrow$ $k_2=\frac{\sigma_k}{\sigma_2}$,
  • $\lambda\geq\lambda_k$ $\Rightarrow$ $k_2=\frac{F_v}{2F_A}$, kde $F_v=\frac{\alpha^2EJ_{min}}{R^2}$.
In [60]:
if lambda_<lambda_k:
  print "kontrola k meznímu stavu pružnosti v tlaku"
  k2=sigma_k_/2/FA_
elif lambda_>=lambda_k:
  print "kontrola k meznímu stavu vzpěrné stability"
  Fv=alpha**2*E_*J_min/r_**2
  k2=Fv/2/F_A_ev
k2

kontrola k meznímu stavu vzpěrné stability
Out[60]:
$$6.62565485782$$

Celková míra bezpečnosti soustavy prutů je,

$$ k=\mathrm{min}\left\{k_1,k_2\right\}, $$
In [62]:
k=np.min([k1,k2])
k
Out[62]:
$$3.76767855531$$

To není marný.

In [ ]: