Anizotropní pružnost - bi-materiálový vrub
Singulární člen
Lechnického, Eshelbyho a Strohův formalismus slouží k vyjádření posuvů a vektoru napětí podél polopřímky vycházející z počátku souřadnic pod úhlem \(\theta\) měřeného od kladné osy \(x\)
(1)\[\begin{split}\begin{equation}
\begin{split}
& \boldsymbol{u}^J(\theta) = \boldsymbol{A}^J\boldsymbol{Z}^J(\theta)\boldsymbol{v}^J
+\overline{\boldsymbol{A}^J}\overline{\boldsymbol{Z}^J}(\theta)\boldsymbol{w}^J, \\
& \boldsymbol{T}^J(\theta) = \boldsymbol{L}^J\boldsymbol{Z}^J(\theta)\boldsymbol{v}^J
+\overline{\boldsymbol{L}^J}\overline{\boldsymbol{Z}^J}(\theta)\boldsymbol{w}^J,
\end{split}
\end{equation}\end{split}\]
kde matice \(\boldsymbol{A}^J\) a \(\boldsymbol{L}^J\) závisí na elastických konstantách a vlastních číslech \(\mu_{1,2}^J\) materiálů \(J=I,II\)
(2)\[\begin{split}\begin{equation}
\begin{split}
& \boldsymbol{L}^J=\left[
\begin{array}{rr}
-\mu_1^J & -\mu_2^J \\
1 & 1
\end{array}
\right], \\
& \boldsymbol{A}^J=\left[
\begin{array}{rr}
s_{11}^\prime\mu_1^2+s_{12}^\prime & s_{11}^\prime\mu_2^2+s_{12}^\prime \\
s_{12}^\prime\mu_1+s_{22}^\prime/\mu_1 & s_{12}^\prime\mu_2+s_{22}^\prime/\mu_2
\end{array}
\right].
\end{split}
\end{equation}\end{split}\]
Vektory \(\boldsymbol{v}^J\) a \(\boldsymbol{w}^J\) jsou neznámé a musí se stanovit z okrajových podmínek úlohy. Nejdříve bude věnována pozornost obecnější úloze, tj. vrubu, jehož rozevření je dáno úhly \(\omega^I\in(0,\pi)\) a \(\omega^{II}\in(-\pi,0)\). Pro úhel \(\theta\) tedy platí
(3)\[\theta\in\big(\omega^{II},\omega^I\big).\]
V případě vrubu, má diagonální matice \(\boldsymbol{Z}^J\big(\omega^J\big)\) tvar
(4)\[\boldsymbol{Z}^J(\theta) = \mathrm{diag}\Big[\big(\cos\theta+\mu^J_1\sin\theta\big)^\delta,
\big(\cos\theta+\mu^J_2\sin\theta\big)^\delta\Big].\]
Ve výše uvedených vztazích (1) je trošku podivnost v zápisu komplexně sdružené diagonální matice \(\overline{\boldsymbol{Z}^J}(\theta)\), kde se nesdružuje exponent \(\delta\) a pro kterou tedy platí
(5)\[\overline{\boldsymbol{Z}^J}(\theta) = \mathrm{diag}\Big[
\big(\cos\theta+\overline{\mu^J_1}\sin\theta\big)^\delta,
\big(\cos\theta+\overline{\mu^J_2}\sin\theta\big)^\delta\Big].\]
V okolí kořene vrubu lze předepsat následující okrajové podmínky
(6)\[\begin{split}\begin{equation}
\begin{split}
& \boldsymbol{T}^I = \boldsymbol{T}^{II} = 0 \quad \mathrm{pro} \quad \theta=\omega^I,\omega^{II}, \\
& \boldsymbol{u}^I = \boldsymbol{u}^{II} \quad \mathrm{pro} \quad \theta=0, \\
& \boldsymbol{T}^I = \boldsymbol{T}^{II} \quad \mathrm{pro} \quad \theta=0.
\end{split}
\end{equation}\end{split}\]
Dosazením vztahů (1) do okrajových podmínek (6) se dostane homogenní systém algebraických rovnic, který se může napsat maticově následovně,
(7)\[\begin{split}\left[
\begin{array}{rrrr}
\boldsymbol{X}^I & \overline{\boldsymbol{X}^I} & \boldsymbol{0} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{0} & \boldsymbol{X}^{II} & \overline{\boldsymbol{X}^{II}} \\
\boldsymbol{I} & \boldsymbol{I} & -\boldsymbol{I} & -\boldsymbol{I} \\
\boldsymbol{B}^I & -\overline{\boldsymbol{B}^I} & -\boldsymbol{B}^{II} & \overline{\boldsymbol{B}^{II}}
\end{array}
\right]
\left[
\begin{array}{r}
\boldsymbol{L}^I\boldsymbol{v}^I \\
\overline{\boldsymbol{L}^I}\boldsymbol{w}^I \\
\boldsymbol{L}^{II}\boldsymbol{v}^{II} \\
\overline{\boldsymbol{L}^{II}}\boldsymbol{w}^{II}
\end{array}
\right]
=\boldsymbol{0},\end{split}\]
kde
(8)\[\begin{split}\begin{equation}
\begin{split}
& \boldsymbol{B}^J = \mathrm{i}\boldsymbol{A}^J\big(\boldsymbol{L}^J\big)^{-1}, \\
& \boldsymbol{X}^J = \boldsymbol{L}^J\boldsymbol{Z}^J\big(\omega^J\big)
\big(\boldsymbol{L}^J\big)^{-1}.
\end{split}
\end{equation}\end{split}\]
Soustava rovnic (7) ze může eliminací proměnných \(\overline{\boldsymbol{L}^I}\boldsymbol{w}^I\), \(\boldsymbol{L}^{II}\boldsymbol{v}^{II}\) a \(\overline{\boldsymbol{L}^{II}}\boldsymbol{w}^{II}\) přepsat do tvaru, viz ,
(9)\[\boldsymbol{K}(\delta)\boldsymbol{L}^J\boldsymbol{v}^J=\boldsymbol{0},\]
kde matice \(\boldsymbol{K}\) má tvar
(10)\[\boldsymbol{K}=\boldsymbol{B}^I+\overline{\boldsymbol{B}^I}\boldsymbol{Y}^I
-\Big(\boldsymbol{B}^{II}
+\overline{\boldsymbol{B}^{II}}\boldsymbol{Y}^{II}\Big)
\big(\boldsymbol{I}-\boldsymbol{Y}^{II}\big)^{-1}
\big(\boldsymbol{I}-\boldsymbol{Y}^I\big)\]
a
(11)\[\boldsymbol{Y}^J = \Big(\overline{\boldsymbol{X}^J}\Big)^{-1} \boldsymbol{X}^J.\]
Zbývá poznamenat stanovení vektoru \(\boldsymbol{v}^{II}\) a \(\boldsymbol{w}^J\), které se určí pomocí vztahu
(12)\[\begin{split}\begin{equation}
\begin{split}
& \boldsymbol{v}^{II} = \big(\boldsymbol{L}^{II}\big)^{-1}\big(\boldsymbol{I}-\boldsymbol{Y}^{II}\big)^{-1}
\big(\boldsymbol{I}-\boldsymbol{Y}^I\big)\boldsymbol{L}^I\boldsymbol{v}^I, \\
& \boldsymbol{w}^J = -\Big(\overline{\boldsymbol{L}^J}\Big)^{-1}
\boldsymbol{Y}^J\boldsymbol{L}^J\boldsymbol{v}^J.
\end{split}
\end{equation}\end{split}\]
Aby soustava (9) měla řešení, musí platit
(13)\[\det\big(\boldsymbol{K}(\delta)\big)=0,\]
odkud se vyjádří exponent \(\delta\). Zpětným dosazením této hodnoty do (9) se spočítá vektor \(\boldsymbol{L}^I\boldsymbol{v}^I\) jako vlastní vektor matice \(\boldsymbol{K}(\delta)\) pro vlastní číslo \(0\). Ze vztahů (12) se následně dopočítají zbývající vektory \(\overline{\boldsymbol{L}^I}\boldsymbol{w}^I\), \(\boldsymbol{L}^{II}\boldsymbol{v}^{II}\) a \(\overline{\boldsymbol{L}^{II}}\boldsymbol{w}^{II}\).
\(T\)-napětí u trhliny na rozhraní
V případě stanovení vztahů pro vyjádření napětí a posuvů (1) v případě tzv. \(T\)-napětí u trhliny, tj. pro
(14)\[\omega^I=\pi \qquad\mathrm{a}\qquad \omega^{II}=-\pi,\]
je trošku komplikovanější, než v případě ostatních exponentů \(\delta\). \(T\)-napětí odpovídá exponent \(\delta=1\), který sice neodpovídá nulové hodnotě determinantu (13), avšak tento determinant je příliš specializovaný. V případě \(T\)-napětí je totiž automaticky splněna druhá rovnost v (6), tj. rovnost posuvů na rozhraní, a matice \(\boldsymbol{K}(\delta)\) soustava rovnic již nejde sestavit.
To, že je exponent \(\delta=1\) řešením úlohy dané okrajovými podmínkami (6), se ukáže velice snadno jeho dosazením do soustavy rovnic (7), jejíž maticový zápis bude mít tvar
(15)\[\begin{split}\left[
\begin{array}{rrrr}
-\boldsymbol{I} & -\boldsymbol{I} & \boldsymbol{0} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{0} & -\boldsymbol{I} & -\boldsymbol{I} \\
\boldsymbol{I} & \boldsymbol{I} & -\boldsymbol{I} & -\boldsymbol{I} \\
\boldsymbol{B}^I & -\overline{\boldsymbol{B}}^I & -\boldsymbol{B}^{II} & \overline{\boldsymbol{B}^{II}}
\end{array}
\right]
\left[
\begin{array}{r}
\boldsymbol{L}^I\boldsymbol{v}^I \\
\overline{\boldsymbol{L}^I}\boldsymbol{w}^I \\
\boldsymbol{L}^{II}\boldsymbol{v}^{II} \\
\overline{\boldsymbol{L}^{II}}\boldsymbol{w}^{II}
\end{array}
\right]
=\boldsymbol{0}\end{split}\]
a která po převodu na horní trojúhelníkovou matici má tvar
(16)\[\begin{split}\left[
\begin{array}{rrrr}
\boldsymbol{I} & \boldsymbol{I} & -\boldsymbol{I} & -\boldsymbol{I} \\
\boldsymbol{0} & -\overline{\boldsymbol{B}^I}-\boldsymbol{B}^I &
-\boldsymbol{B}^{II}+\boldsymbol{B}^I & \overline{\boldsymbol{B}^{II}}+\boldsymbol{B}^I\\
\boldsymbol{0} & \boldsymbol{0} & \boldsymbol{I} & \boldsymbol{I} \\
\boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0}
\end{array}
\right].\end{split}\]
Z ní jde vidět, že determinant matice soustavy (15) je nulový a dále, že je tento exponent dvojnásobný. To dokazuje nulový poslední řádek v matici, který odpovídá faktu, že vlastní vektory matice \(\boldsymbol{L}^I\boldsymbol{v}^I\) závisí na vektoru \(\overline{\boldsymbol{L}^{II}}\boldsymbol{w}^{II}\) a naopak. Každý z těchto vektorů jde vyjádřit jako lineární kombinaci dvou nezávislých složek. Odtud násobnost exponentu \(\delta=1\). Lépe to jde vidět ze soustavy, která se získá eliminací \(\overline{\boldsymbol{L}^I}\boldsymbol{w}^I\) a \(\overline{\boldsymbol{L}^{II}}\boldsymbol{w}^{II}\)
(17)\[\Big(\boldsymbol{B}^I+\overline{\boldsymbol{B}^I}\Big)\boldsymbol{L}^I\boldsymbol{v}^I
-\Big(\boldsymbol{B}^{II}+\overline{\boldsymbol{B}^{II}}\Big)
\boldsymbol{L}^{II}\boldsymbol{v}^{II}=\boldsymbol{0}.\]
Vektor \(\boldsymbol{L}^I\boldsymbol{v}^I\) nebo \(\boldsymbol{L}^{II}\boldsymbol{v}^{II}\) se musí zvolit, aby se mohly zbývající vektory určit. V každém případě jde zvolit vždy dva lineárně nezávislé tvary těchto vektorů, tak např.
(18)\[\boldsymbol{L}^I\boldsymbol{v}^I = [\begin{array}{ll} \mathrm{i} & 0 \end{array}]^T\]
a
(19)\[\boldsymbol{L}^I\boldsymbol{v}^I = [\begin{array}{ll} 0 & \mathrm{i} \end{array}]^T.\]
Vektory \(\boldsymbol{L}^{II}\boldsymbol{v}^{II}\) se dostanou dosazením těchto vektorů do (17)
(20)\[\boldsymbol{L}^{II}\boldsymbol{v}^{II}=
\Big(\boldsymbol{B}^{II}+\overline{\boldsymbol{B}^{II}}\Big)^{-1}
\Big(\boldsymbol{B}^I+\overline{\boldsymbol{B}^I}\Big)\boldsymbol{L}^I\boldsymbol{v}^I\]
Zbývající vektory se dostanou z první a druhé soustavy rovnic matice (15),
(21)\[\overline{\boldsymbol{L}^I}\boldsymbol{w}^I=-\boldsymbol{L}^I\boldsymbol{v}^I\]
a
(22)\[\overline{\boldsymbol{L}^{II}}\boldsymbol{w}^{II}=-\boldsymbol{L}^{II}\boldsymbol{v}^{II}.\]
V je uvedeno, že v případě reálného exponentu, což je i zde probíraný případ \(\delta=1\), platí
(23)\[\boldsymbol{w}^J=\overline{\boldsymbol{v}^J}.\]
Odtud a z (21) a (22) pro \(J=I,II\) plyne
(24)\[\overline{\boldsymbol{L}^J}\boldsymbol{w}^J=\overline{\boldsymbol{L}^J\boldsymbol{v}^J}
=-\boldsymbol{L}^J\boldsymbol{v}^J,\]
nebo-li
(25)\[ \overline{\boldsymbol{L}^J\boldsymbol{v}^J}+\boldsymbol{L}^J\boldsymbol{v}^J=\Re\big\{\boldsymbol{L}^J\boldsymbol{v}^J\big\}=0.\]
Tedy \(\boldsymbol{L}^J\boldsymbol{v}^J\) jsou ryze imaginární. Odtud podivná volba komplexních jednotek v (18) a (19).
Složky napětí, včetně \(T\)-napětí, pro \(\delta=1\) se mohou vyjádřit následovně, viz ,
(26)\[\begin{split}\begin{equation}
\begin{split}
\boldsymbol{\sigma}_1^J =& -\boldsymbol{L}^J\boldsymbol{M}^J\boldsymbol{I}\big(\boldsymbol{L}^J\big)^{-1}
\boldsymbol{L}^J\boldsymbol{v}^J
-\overline{\boldsymbol{L}^J}\overline{\boldsymbol{M}^J}\boldsymbol{I}
\big(\overline{\boldsymbol{L}^J}\big)^{-1}
\overline{\boldsymbol{L}^J}\overline{\boldsymbol{v}^J} \\
=& -\boldsymbol{L}^J\boldsymbol{M}^J\big(\boldsymbol{L}^J\big)^{-1}
\boldsymbol{L}^J\boldsymbol{v}^J
-\overline{\boldsymbol{L}^J}\overline{\boldsymbol{M}^J}
\big(\overline{\boldsymbol{L}^J}\big)^{-1}
\overline{\boldsymbol{L}^J}\overline{\boldsymbol{v}^J} \\
\boldsymbol{\sigma}_2^J =& \boldsymbol{L}^J\boldsymbol{I}\big(\boldsymbol{L}^J\big)^{-1}
\boldsymbol{L}^J\boldsymbol{v}^J
+\overline{\boldsymbol{L}^J}\boldsymbol{I}
\big(\overline{\boldsymbol{L}^J}\big)^{-1}
\overline{\boldsymbol{L}^J}\overline{\boldsymbol{v}^J} \\
=& \boldsymbol{L}^J\boldsymbol{v}^J
+\overline{\boldsymbol{L}^J}\overline{\boldsymbol{v}^J},
\end{split}
\end{equation}\end{split}\]
kde
(27)\[\begin{split}\boldsymbol{M}=\left[
\begin{array}{rr}
\mu_1^J & 0 \\
0 & \mu_2^J
\end{array}
\right].\end{split}\]
Jestliže se vezme v úvahu, že
(28)\[\begin{split}\boldsymbol{L}^J\boldsymbol{M}^J\big(\boldsymbol{L}^J\big)^{-1}=
\left[
\begin{array}{rr}
\mu_1^J+\mu_2^J & -\mu_1^J\mu_2^J \\
-1 & 0
\end{array}
\right],\end{split}\]
pak na základě (18) a (19) se pro napětí \(\sigma_1^I\) a \(\sigma_2^I\) podle (26) může psát
(29)\[\begin{split}\begin{equation}
\begin{split}
\left[
\begin{array}{l}
T^I \\
0
\end{array}
\right]
=&
-\left[
\begin{array}{rr}
\mu_1^I+\mu_2^I & -\mu_1^I\mu_2^I \\
-1 & 0
\end{array}
\right]
\left(t_1\left[
\begin{array}{r}
\mathrm{i} \\
0
\end{array}
\right]+t_2\left[
\begin{array}{r}
0 \\
\mathrm{i}
\end{array}
\right]
\right) \\
& -\left[
\begin{array}{rr}
\overline{\mu_1^I}+\overline{\mu_2^I} & -\overline{\mu_1^I}\overline{\mu_2^I} \\
-1 & 0
\end{array}
\right]
\left(\overline{t_1}\left[
\begin{array}{r}
-\mathrm{i} \\
0
\end{array}
\right]+\overline{t_2}\left[
\begin{array}{r}
0 \\
-\mathrm{i}
\end{array}
\right]
\right) \\
\left[
\begin{array}{l}
0 \\
0
\end{array}
\right]
=&
t_1\left[
\begin{array}{r}
\mathrm{i} \\
0
\end{array}
\right]+t_2\left[
\begin{array}{r}
0 \\
\mathrm{i}
\end{array}
\right]+\overline{t_1}\left[
\begin{array}{r}
-\mathrm{i} \\
0
\end{array}
\right]+\overline{t_2}\left[
\begin{array}{r}
0 \\
-\mathrm{i}
\end{array}
\right],
\end{split}
\end{equation}\end{split}\]
kde se obecně komplexní koeficienty \(t_1\) a \(t_2\) určí pomocí procedury dané \(\Psi\)-integrálem. Z druhé soustavy rovnic v (29) se dostane, že \(t_1\) a \(t_2\) jsou reálné
(30)\[\begin{split}\begin{equation}
\begin{split}
& 0 = t_1 - \overline{t_1} \quad \Rightarrow \quad \Im\big\{t_1\big\}=0, \\
& 0 = t_2 - \overline{t_2} \quad \Rightarrow \quad \Im\big\{t_2\big\}=0.
\end{split}
\end{equation}\end{split}\]
Druhá rovnice první soustavy rovnic (29) je pak splněna automaticky a z první rovnice plyne hodnota \(T^I\)-napětí
(31)\[T^I=2\Big(t_1\Im\big\{\mu_1^I+\mu_2^I\big\}-t_2\Im\big\{\mu_1^I\mu_2^I\big\}\Big).\]
K vyjádření \(T^{II}\)-napětí je nutné vyjádřit reálnou část matice \(\boldsymbol{B}^J\). Ta má tvar
(32)\[\begin{split}\boldsymbol{B}^J=\mathrm{i}\left[
\begin{array}{rr}
-s_{11}^{\prime J}\big(\mu_1^J+\mu_2^J\big) &
-s_{11}^{\prime J}\mu_1^J\mu_2^J+s_{12}^{\prime J} \\
-s_{12}^{\prime J}+s_{22}^{\prime J}/\mu_1^J\mu_2^J &
s_{22}^{\prime J}\big(\mu_1^J+\mu_2^J\big)/\mu_1^J\mu_2^J
\end{array}
\right].\end{split}\]
Její reálná část a její inverze má tvar
(33)\[\begin{split}\boldsymbol{B}^J+\overline{\boldsymbol{B}^J}
=2\left[
\begin{array}{rr}
s_{11}^{\prime J}\Im\big\{\mu_1^J+\mu_2^J\big\} & s_{11}^{\prime J}\Im\big\{\mu_1^J\mu_2^J\big\} \\
-s_{22}^{\prime J}\Im\big\{1/\mu_1^J\mu_2^J\big\} &
-s_{22}^{\prime J}\Im\big\{\big(\mu_1^J+\mu_2^J\big)/\mu_1^J\mu_2^J\big\}
\end{array}
\right],\end{split}\]
(34)\[\begin{split}\begin{equation}
\begin{split}
& \big(\boldsymbol{B}^J+\overline{\boldsymbol{B}^J}\big)^{-1} = \\
& \qquad =
\frac{1}{\det\big(\boldsymbol{B}^J+\overline{\boldsymbol{B}^J}\big)}
\left[
\begin{array}{rr}
-s_{22}^{\prime J}\Im\big\{\big(\mu_1^J+\mu_2^J\big)/\mu_1^J\mu_2^J\big\} &
s_{11}^{\prime J}\Im\big\{\mu_1^J\mu_2^J\big\} \\
-s_{22}^{\prime J}\Im\big\{1/\mu_1^J\mu_2^J\big\} & s_{11}^{\prime J}\Im\big\{\mu_1^J+\mu_2^J\big\}
\end{array}
\right],
\end{split}
\end{equation}\end{split}\]
kde
(35)\[\begin{split}\begin{equation}
\begin{split}
& \det\big(\boldsymbol{B}^J+\overline{\boldsymbol{B}^J}\big) = \\
& \qquad =
2s_{11}^{\prime J}s_{22}^{\prime J}\Bigg(-\Im\big\{\mu_1^J
+\mu_2^J\big\}\Im\Bigg\{\frac{\mu_1^J+\mu_2^J}{\mu_1^J\mu_2^J}\Bigg\}
+\Im\big\{\mu_1^J\mu_2^J\big\}\Im\Bigg\{\frac{1}{\mu_1^J\mu_2^J}\Bigg\}\Bigg).
\end{split}
\end{equation}\end{split}\]
Podle (20) potom pro \(\boldsymbol{L}^{II}\boldsymbol{v}^{II}\) platí
(36)\[\begin{split}\begin{equation}
\begin{split}
\boldsymbol{L}^{II}\boldsymbol{v}^{II} =&
\big(\boldsymbol{B}^{II}+\overline{\boldsymbol{B}^{II}}\big)^{-1}
\big(\boldsymbol{B}^I+\overline{\boldsymbol{B}^I}\big)\left(t_1\left[
\begin{array}{r}
\mathrm{i} \\
0
\end{array}
\right]+t_2\left[
\begin{array}{r}
0 \\
\mathrm{i}
\end{array}
\right]\right) \\
=& \frac{2\mathrm{i}}{\det\big(\boldsymbol{B}^{II}+\overline{\boldsymbol{B}^{II}}\big)} \\
& \times
\left(t_1\left[
\begin{array}{r}
-s_{22}^{II}s_{11}^I\Im\big\{\big(\mu_1^{II}+\mu_2^{II}\big)/\mu_1^{II}\mu_2^{II}\big\}
\Im\big\{\mu_1^I+\mu_2^I\big\} \\
s_{22}^{II}s_{11}^I\Im\big\{1/\mu_1^{II}\mu_2^{II}\big\}
\Im\big\{\mu_1^I+\mu_2^I\big\}
\end{array}
\right.
\right. \\
& \qquad\qquad\qquad\qquad\qquad
\left.
\begin{array}{r}
+s_{11}^{II}s_{22}^I\Im\Big\{\mu_1^{II}\mu_2^{II}\Big\}
\Im\big\{1/\mu_1^I\mu_2^I\big\} \\
-s_{11}^{II}s_{22}^I\Im\big\{\mu_1^{II}+\mu_2^{II}\big\}
\Im\big\{1/\mu_1^I\mu_2^I\big\}
\end{array}
\right] \\
& \qquad
+t_2\left[
\begin{array}{r}
-s_{22}^{II}s_{11}^I\Im\big\{\big(\mu_1^{II}+\mu_2^{II}\big)/\mu_1^{II}\mu_2^{II}\big\}
\Im\big\{\mu_1^I\mu_2^I\big\} \\
s_{22}^{II}s_{11}^I\Im\big\{1/\mu_1^{II}\mu_2^{II}\big\}
\Im\big\{\mu_1^I\mu_2^I\big\}
\end{array}
\right. \\
& \left.\qquad\qquad\qquad
\left.
\begin{array}{r}
+s_{11}^{II}s_{22}^I\Im\Big\{\mu_1^{II}\mu_2^{II}\Big\}
\Im\big\{\big(\mu_1^I+\mu_2^I\big)/\mu_1^I\mu_2^I\big\} \\
+s_{11}^{II}s_{22}^I\Im\big\{\mu_1^{II}+\mu_2^{II}\big\}
\Im\big\{\big(\mu_1^I+\mu_2^I\big)/\mu_1^I\mu_2^I\big\}
\end{array}
\right]
\right)
\end{split}
\end{equation}\end{split}\]
Dosazením \(\boldsymbol{L}^{II}\boldsymbol{v}^{II}\) do první rovnice vztahu \(\boldsymbol{\sigma}_1^J\) v soustavě (26) se může podobně jako \(T^I\) vyjádřit také \(T^{II}\)-napětí
(37)\[T^{II}=2\Big(t_1^{II}\Im\big\{\mu_1^{II}+\mu_2^{II}\big\}-t_2^{II}\Im\big\{\mu_1^{II}\mu_2^{II}\big\}\Big),\]
kde
(38)\[\begin{split}\begin{equation}
\begin{split}
t_1^{II} =& \frac{2}{\det\big(\boldsymbol{B}^{II}+\overline{\boldsymbol{B}^{II}}\big)} \\
& \times
\Big[
t_1
\big(-s_{22}^{II}s_{11}^I\Im\big\{\big(\mu_1^{II}+\mu_2^{II}\big)/\mu_1^{II}\mu_2^{II}\big\}
\Im\big\{\mu_1^I+\mu_2^I\big\} \\
& \qquad
+s_{11}^{II}s_{22}^I\Im\Big\{\mu_1^{II}\mu_2^{II}\Big\}
\Im\big\{1/\mu_1^I\mu_2^I\big\}\big) \\
& \quad
+t_2
\big(-s_{22}^{II}s_{11}^I\Im\big\{\big(\mu_1^{II}+\mu_2^{II}\big)/\mu_1^{II}\mu_2^{II}\big\}
\Im\big\{\mu_1^I\mu_2^I\big\} \\
& \qquad
+s_{11}^{II}s_{22}^I\Im\Big\{\mu_1^{II}\mu_2^{II}\Big\}
\Im\big\{\big(\mu_1^I+\mu_2^I\big)/\mu_1^I\mu_2^I\big\}\big)
\Big], \\
t_2^{II} =& \frac{2}{\det\big(\boldsymbol{B}^{II}+\overline{\boldsymbol{B}^{II}}\big)} \\
& \times
\Big[
t_1
\big(s_{22}^{II}s_{11}^I\Im\big\{1/\mu_1^{II}\mu_2^{II}\big\}
\Im\big\{\mu_1^I+\mu_2^I\big\} \\
& \qquad
-s_{11}^{II}s_{22}^I\Im\big\{\mu_1^{II}+\mu_2^{II}\big\}
\Im\big\{1/\mu_1^I\mu_2^I\big\}\big) \\
& \quad
+t_2
\big(s_{22}^{II}s_{11}^I\Im\big\{1/\mu_1^{II}\mu_2^{II}\big\}
\Im\big\{\mu_1^I\mu_2^I\big\} \\
& \qquad
+s_{11}^{II}s_{22}^I\Im\big\{\mu_1^{II}+\mu_2^{II}\big\}
\Im\big\{\big(\mu_1^I+\mu_2^I\big)/\mu_1^I\mu_2^I\big\}\big)
\Big]
\end{split}
\end{equation}\end{split}\]
Pomocné řešení pro T-napětí u trhliny na rozhraní
Pomocné řešení pro \(T\)-napětí pro trhlinu na rozhraní má exponent \(\delta=-1\) a pro odpovídající vlastní vektory platí totožné vztahy (18)-(25) jako pro vlastní vektory standardního řešení. Postupnou aplikací těchto pomocných vektorů do algoritmu výpočtu \(\Psi\)-integrálu se vyjádří konstanta \(t_1\) u vektoru
(39)\[\boldsymbol{L}^I\boldsymbol{v}^I = [\begin{array}{ll} \mathrm{i} & 0 \end{array}]^T\]
a konstanta \(t_2\) u vektoru
(40)\[\boldsymbol{L}^I\boldsymbol{v}^I = [\begin{array}{ll} 0 & \mathrm{i} \end{array}]^T\]
standardního řešení. Na základě poznámek uvedených výše musí být tyto konstanty reálné.
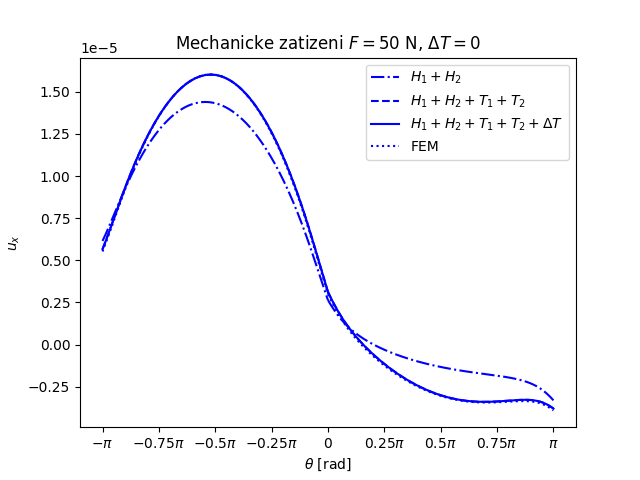
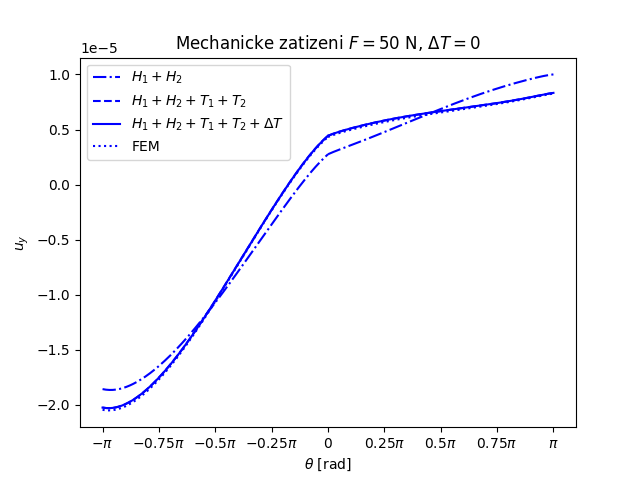
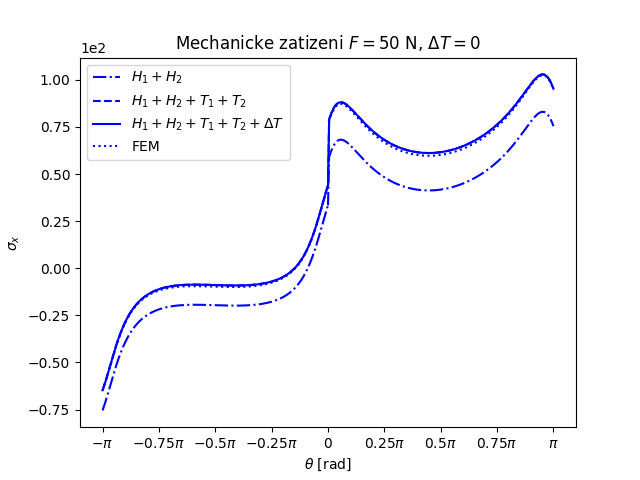
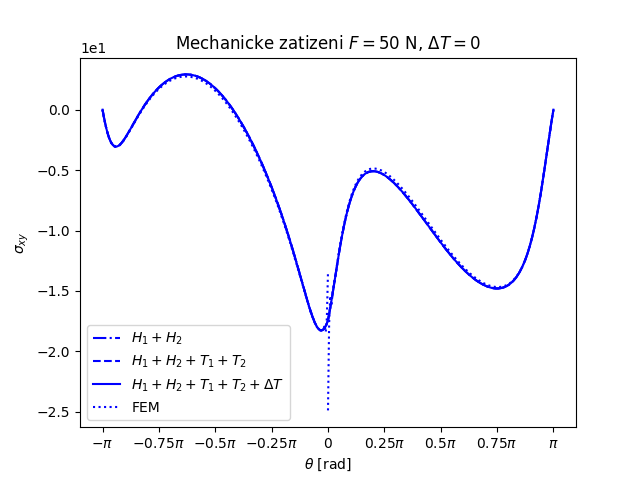
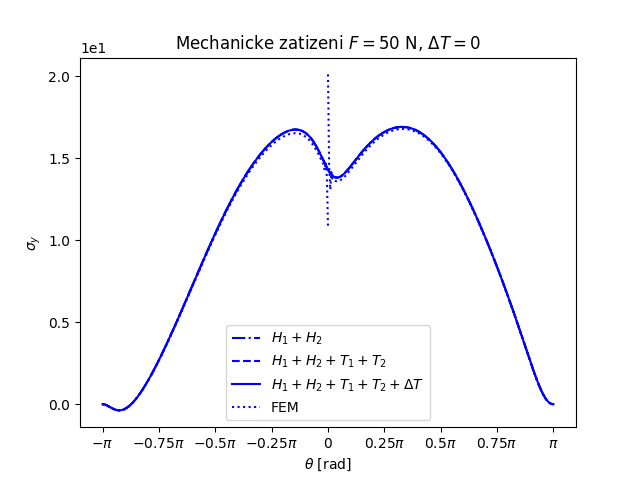
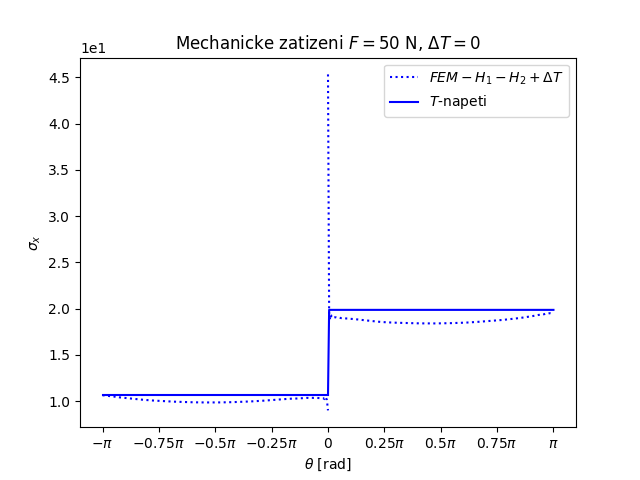
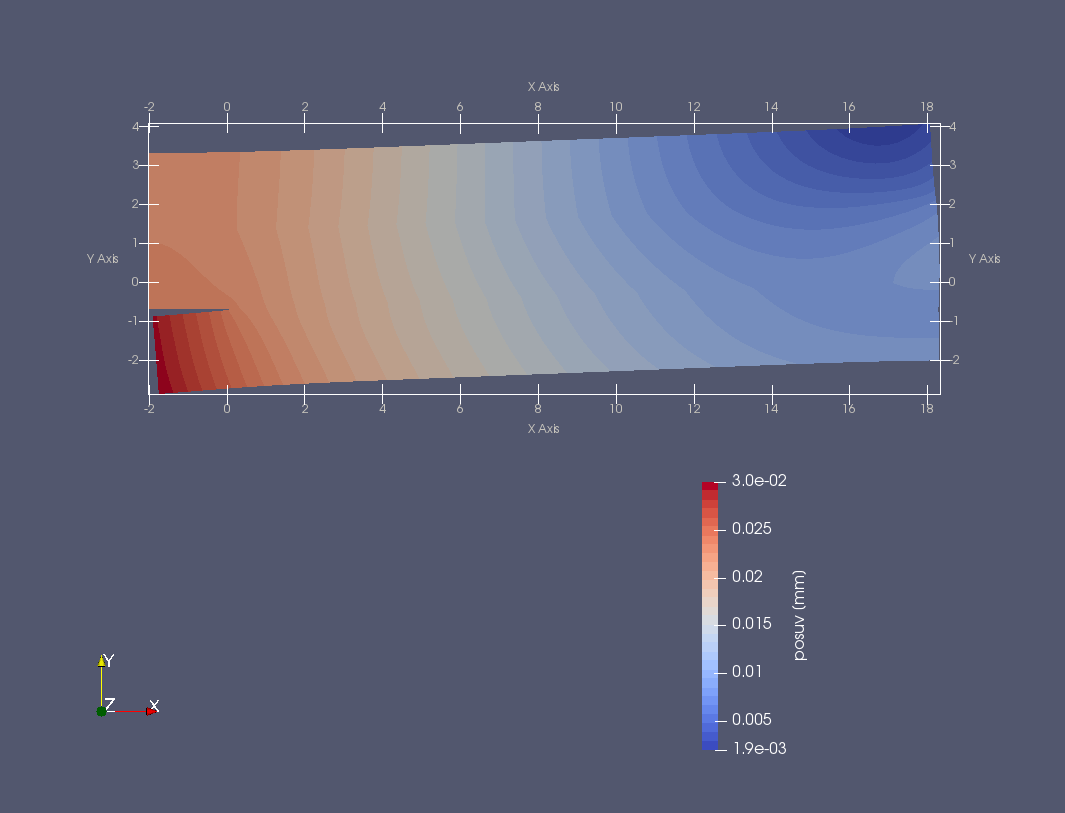
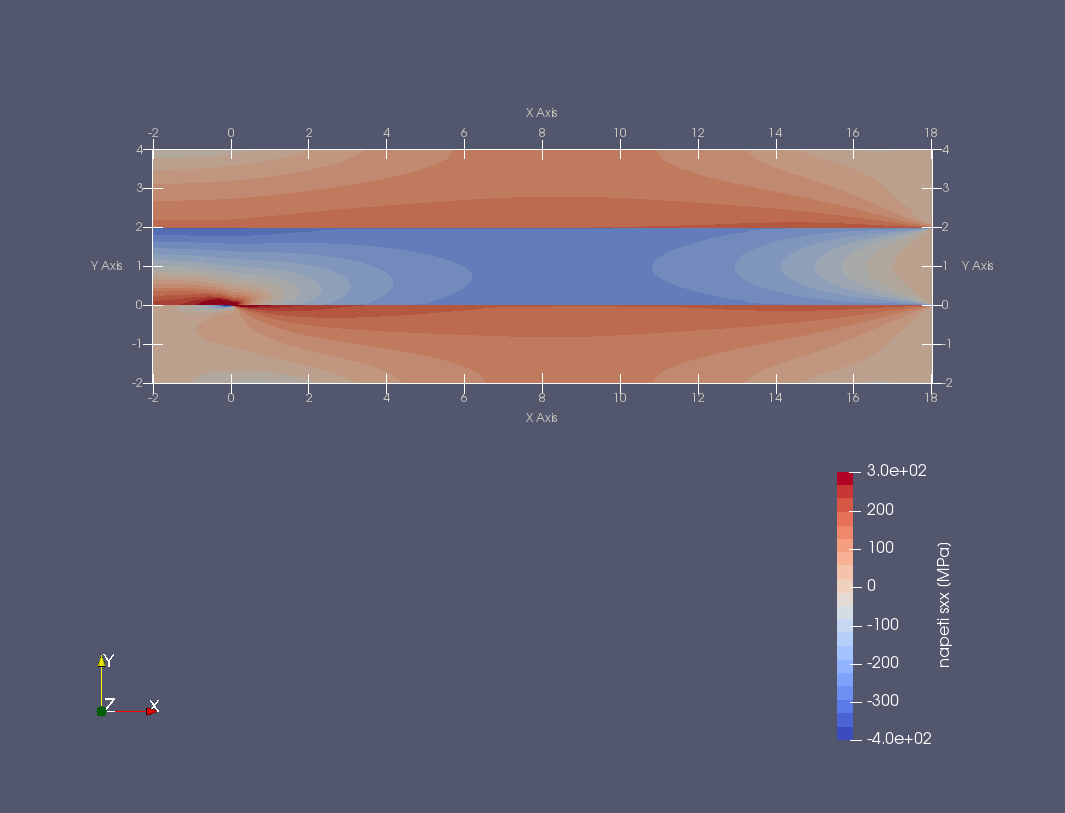
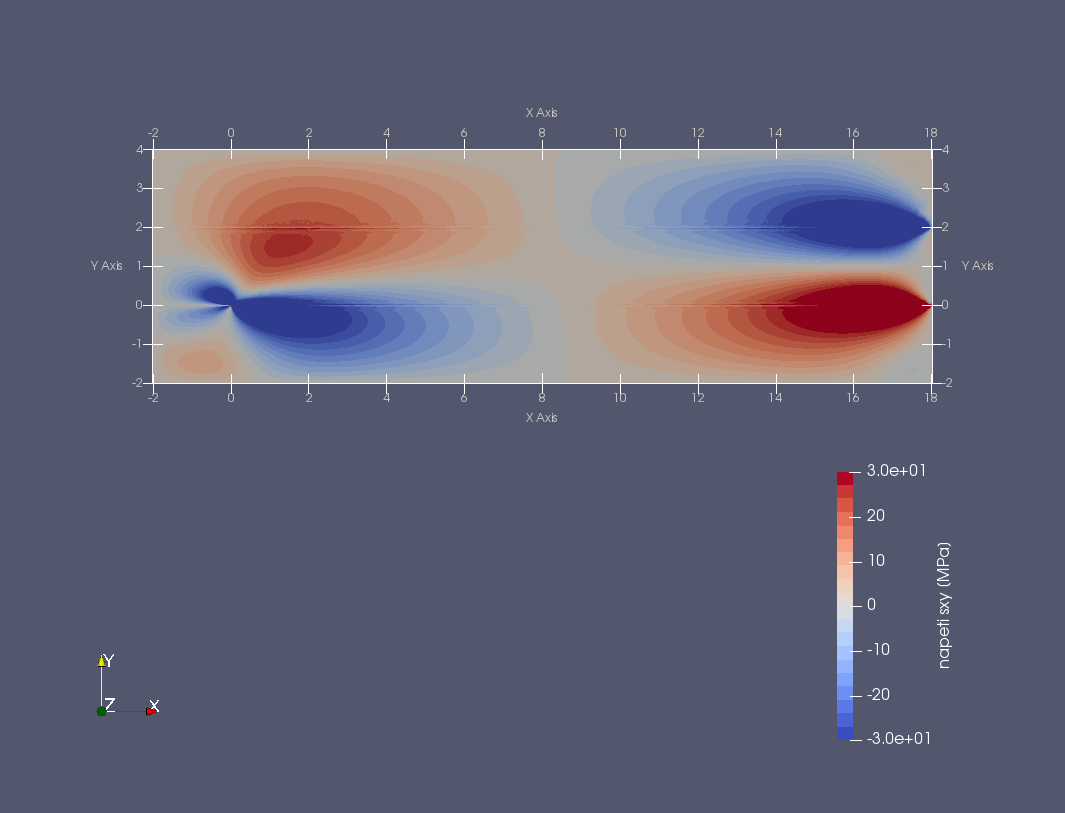
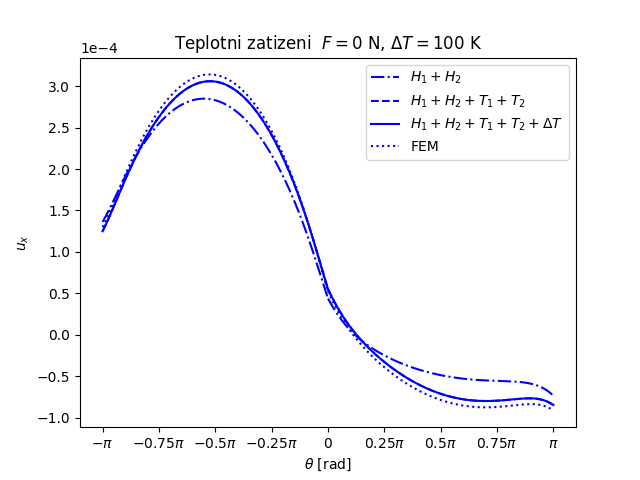
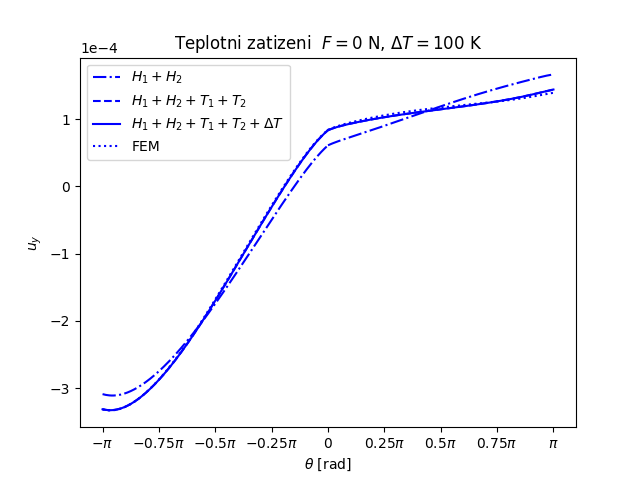
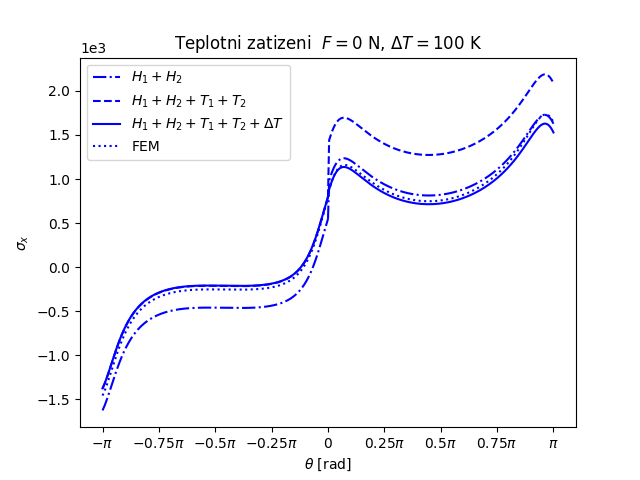
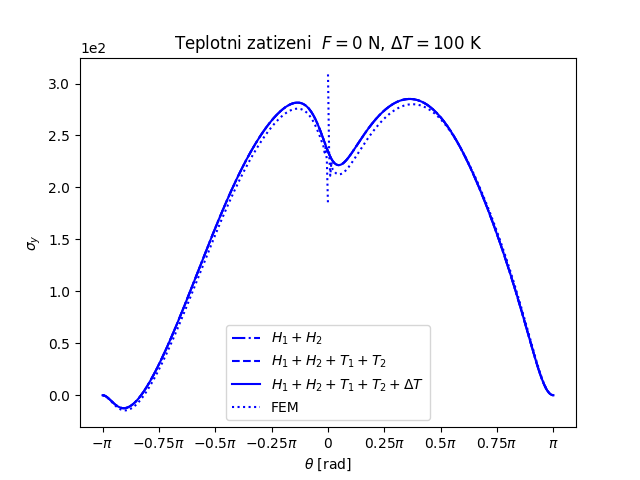
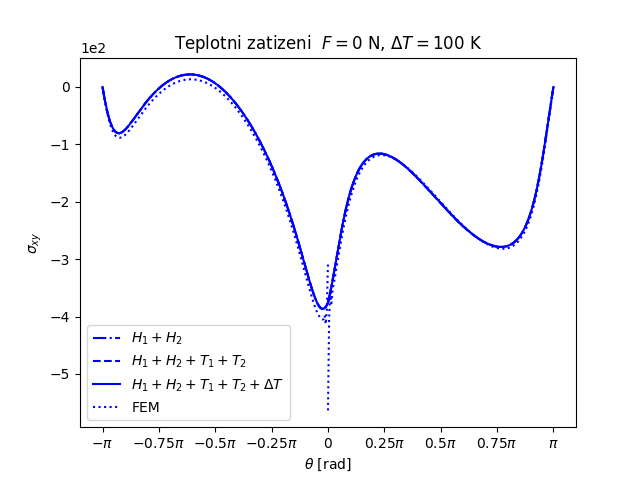
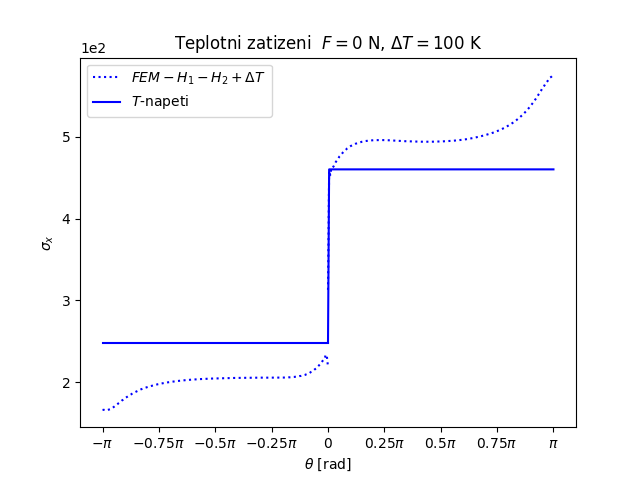
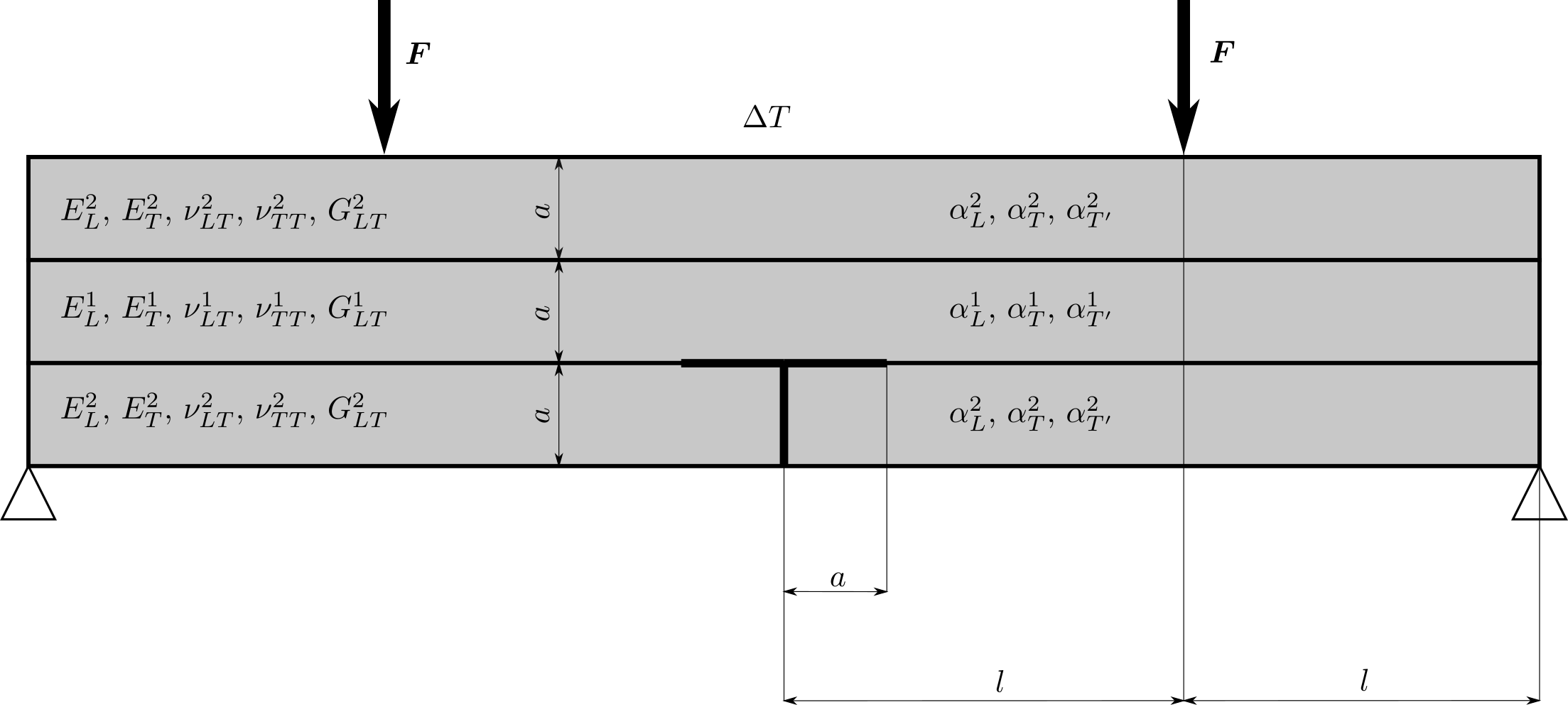
Trhlina na rozhraní dvou monoklinických materiálů namáhaných čtyřbodovým ohybem a teplotním zatížením (FEniCS 2018.1.0)
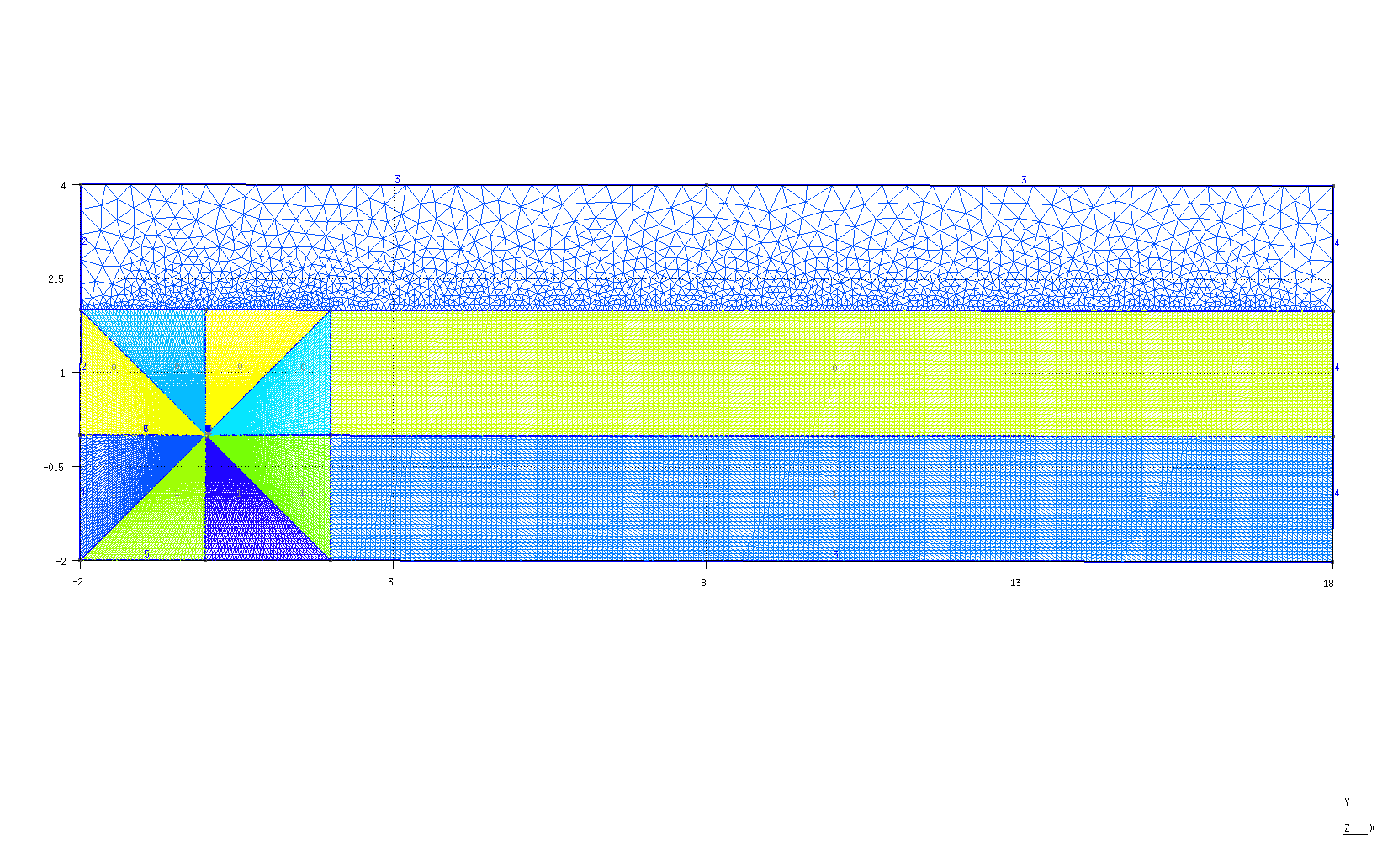
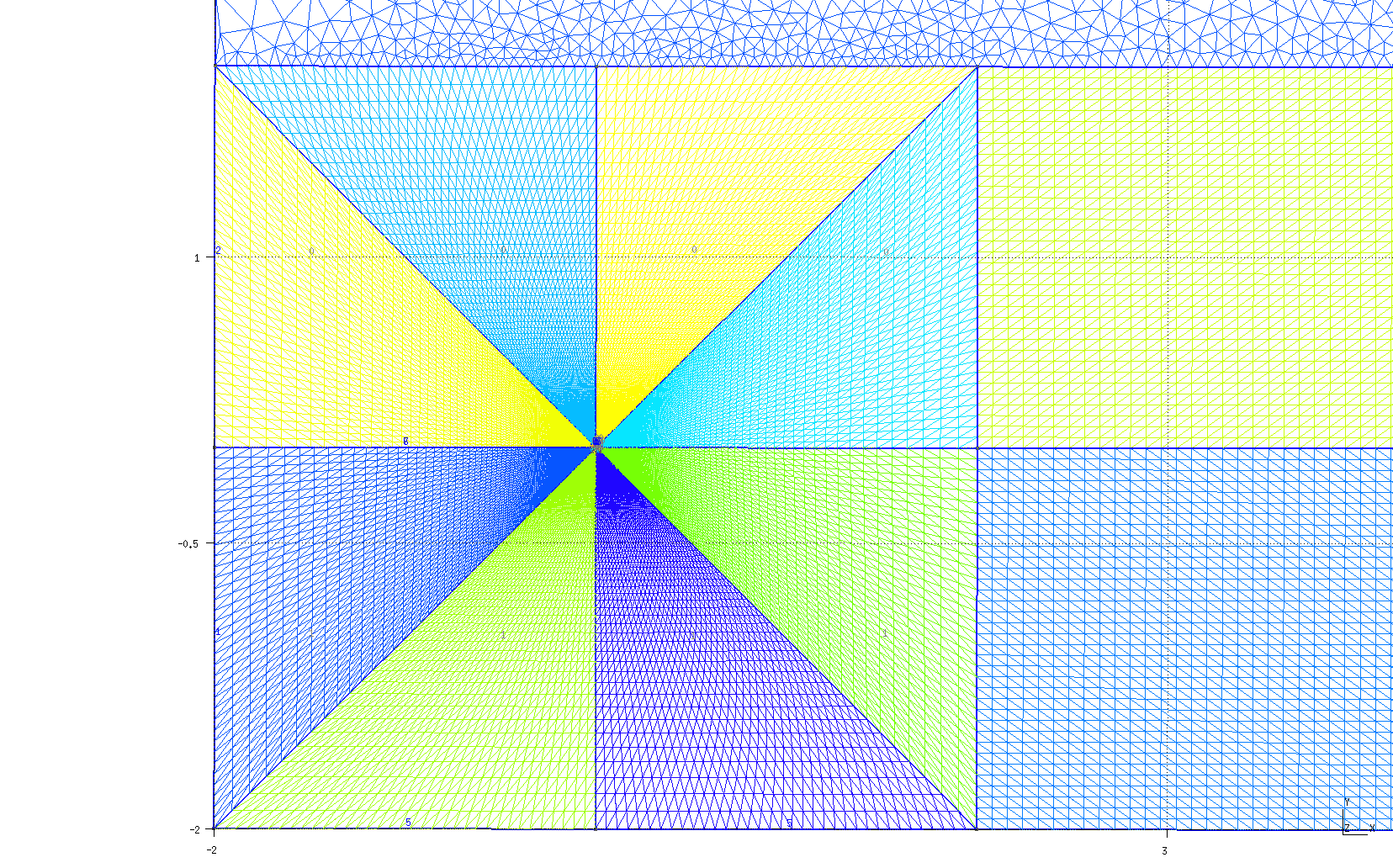
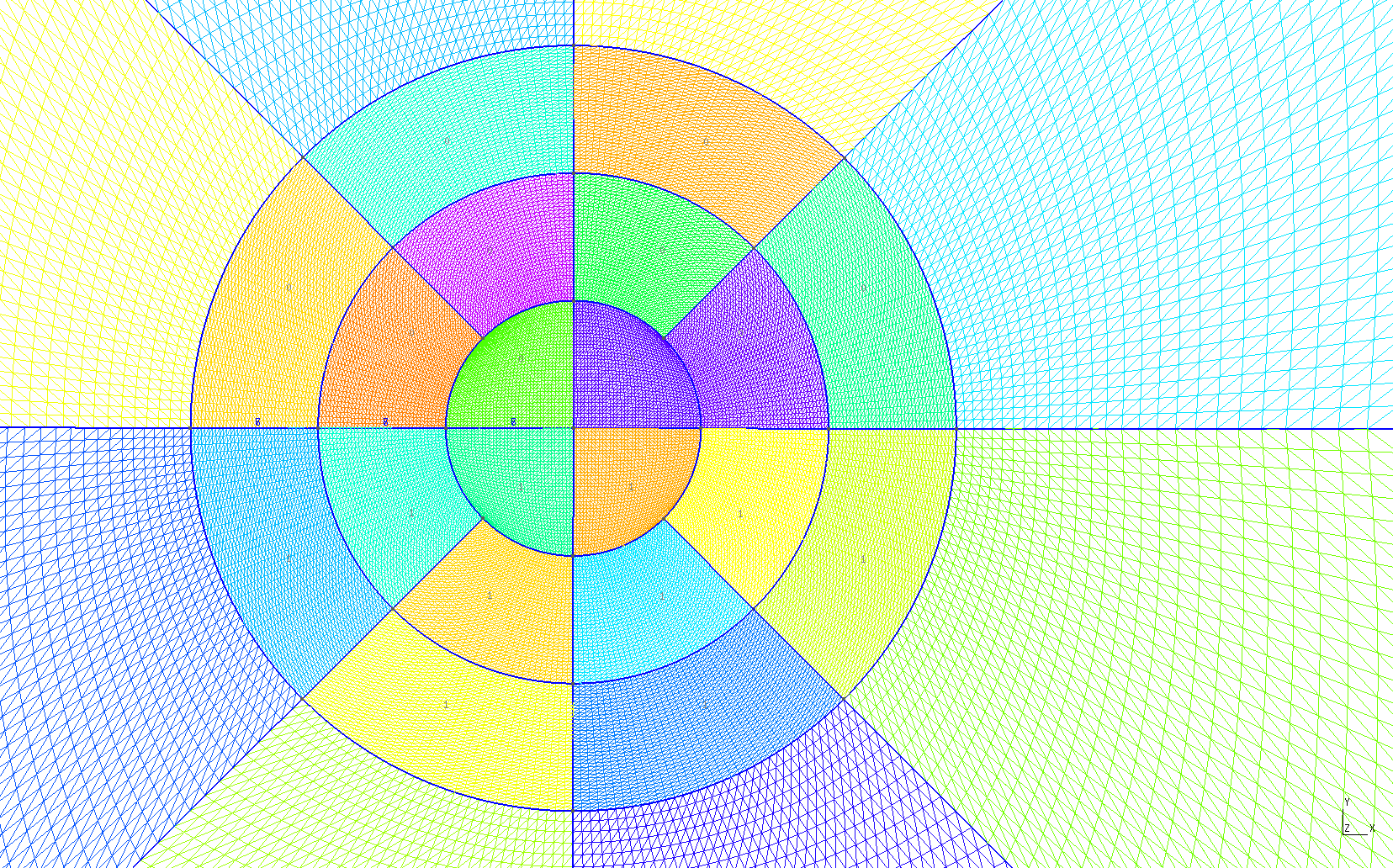
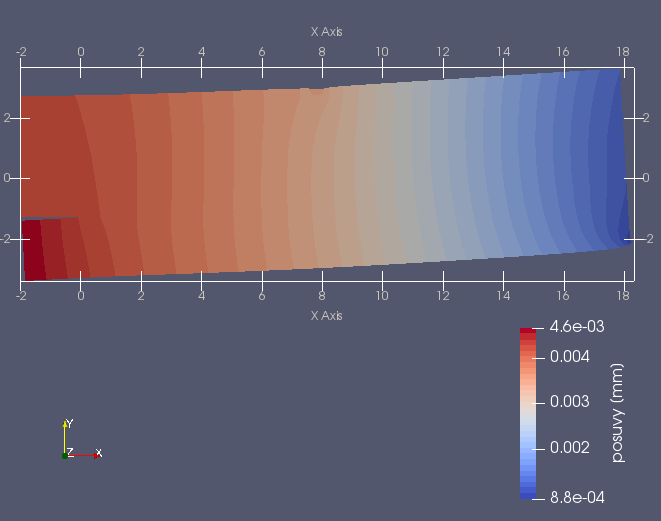
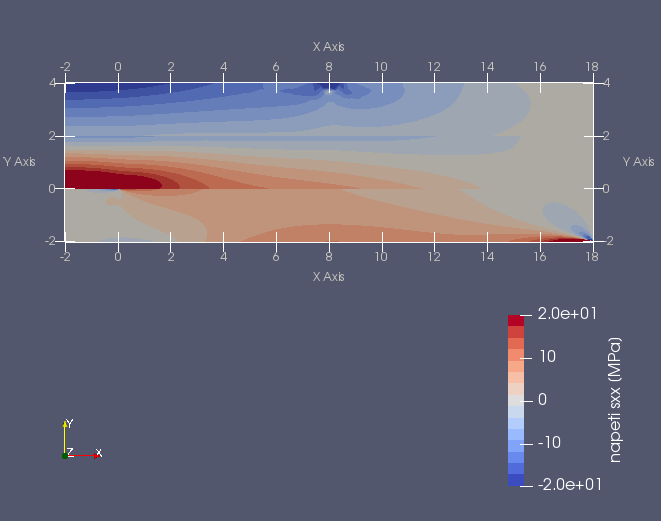
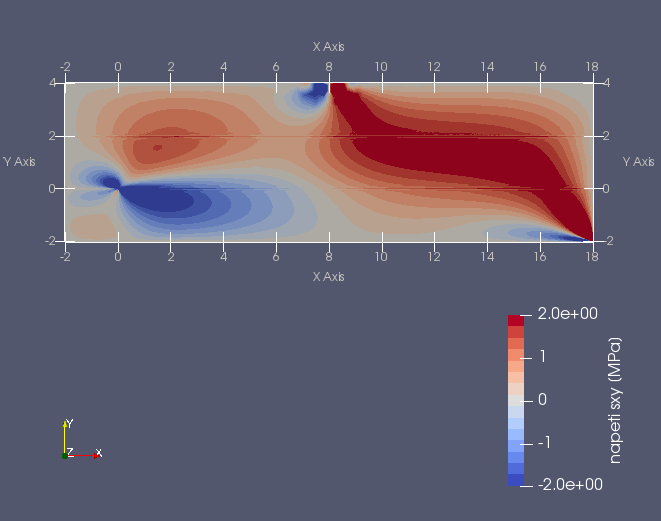
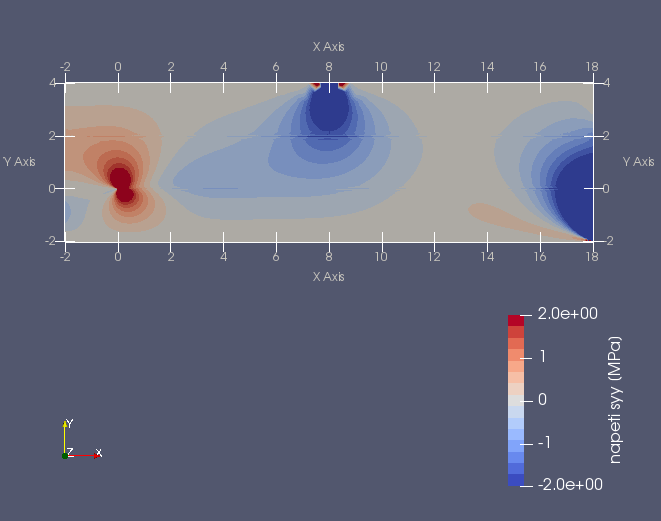
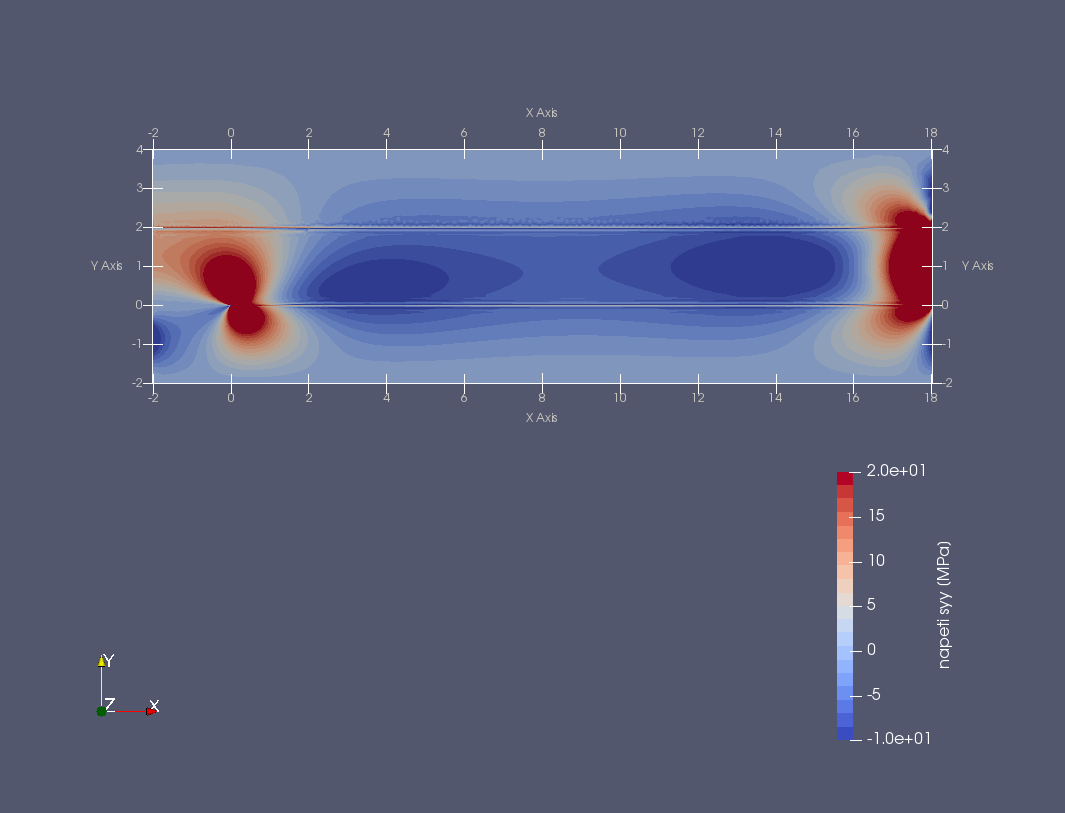
Další příklad trhliny na rozhraní dvou anizotropních materiálů nabízí následující úloha. Prut (vzorek) složený ze tří vrstev anizotropních materiálů namáhaný čtyřbodovým ohybem má v nejnižší nejvíce namáhané vrstvě příčnou magistrální trhlinu, která se rozdělila do dvou marginálních trhlin šířících se podél rozhraní mezi vrstvami vzorku, viz následující obrázek.
Kromě mechanického zatížení je vzorek zatížený i teplotně. Při zatížení teplotou má Hookeův zákon v případě zobecněné rovinné deformace tvar
(41)\[\boldsymbol{\varepsilon}=\boldsymbol{S}\boldsymbol{\sigma}+\boldsymbol{\varepsilon}_{\Delta T},\]
kde
(42)\[\begin{split}\boldsymbol{\varepsilon}=\left[\begin{array}{l}
\varepsilon_{xx} \\ \varepsilon_{yy} \\ 2\varepsilon_{xy}
\end{array}\right], \quad
\boldsymbol{\sigma}=\left[\begin{array}{l} \sigma_{xx} \\ \sigma_{yy} \\ \sigma_{xy} \end{array}\right], \quad
\boldsymbol{\varepsilon}_{\Delta T}=
\left[\begin{array}{l}
\bigg(\alpha_L+\frac{\nu_{LT}\alpha_{T'}E_T}{E_L}\bigg)\Delta T \\
\big(\alpha_T+\nu_{TT'}\alpha_{T'}\big)\Delta T \\
0
\end{array}
\right],\end{split}\]
(43)\[\begin{split}\boldsymbol{S}=\left[\begin{array}{lll}
\bigg(1-\frac{\nu_{LT}^2E_T}{E_L}\bigg)\frac{1}{E_L}
& -\big(1+\nu_{TT'}\big)\frac{\nu_{LT}}{E_L} & 0 \\
-\big(1+\nu_{TT'}\big)\frac{\nu_{LT}}{E_L} & \big(1-\nu_{TT'}^2\big)\frac{1}{E_T} & 0 \\
0 & 0 & \frac{1}{G_{LT}}
\end{array}\right]\end{split}\]
kde \(\Delta T\), \(\alpha_L\), \(\alpha_T\) a \(\alpha_{T'}\) jsou rozdíl teplot a teplotní roztažnosti ve směrech os \(x\), \(y\) a \(z\). Pro FEniCS je nutné použít inverzní tvar výše uvedeného Hookeova zákona
(44)\[\boldsymbol{\sigma}=\boldsymbol{C}\big(\boldsymbol{\varepsilon}-\boldsymbol{\varepsilon}_{\Delta T}\big),\]
kde
(45)\[\boldsymbol{C}=\boldsymbol{S}^{-1}.\]
Slabá formulace úlohy se pak může napsat následovně
(46)\[\int_\Omega\boldsymbol{\sigma}:\delta\boldsymbol{\varepsilon}\mathrm{d}\Omega
-\int_\Omega\boldsymbol{\sigma}_{\Delta T}:\delta\boldsymbol{\varepsilon}\mathrm{d}\Omega
-\int_{\partial\Omega}\boldsymbol{t}\cdot\delta\boldsymbol{u}\mathrm{d}\partial\Omega=0,\]
kde
(47)\[\boldsymbol{\sigma}_{\Delta T}=\boldsymbol{C}\boldsymbol{\varepsilon}_{\Delta T}.\]
a
(48)\[\boldsymbol{t}=\boldsymbol{\sigma}\cdot\boldsymbol{n}\]
je vektor napětí, \(\boldsymbol{n}\) je vnější normála k hranici \(\delta\Omega\) a \(\boldsymbol{u}\) jsou posuvy, pro které platí
(49)\[\boldsymbol{\varepsilon}=\frac{1}{2}(\nabla\boldsymbol{u}+\boldsymbol{u}\nabla).\]
Asymptotický rozvoj napětí a posuvů před čelem trhliny
Posuvy a napětí před čelem trhliny se mohou napsat ve tvaru asymptotického rozvoje
(50)\[\begin{split}\begin{equation}
\begin{split}
\boldsymbol{\sigma}_1^J =&
-2\Re\big\{H_\delta\boldsymbol{L}^J\boldsymbol{M}^J\boldsymbol{Z}_\delta^{\prime J}
\boldsymbol{v}_\delta^J\big\}
-2\Re\big\{H_{-\delta}\boldsymbol{L}^J\boldsymbol{M}^J\boldsymbol{Z}_{-\delta}^{\prime J}
\boldsymbol{v}_{-\delta}^J\big\} \\
& +\boldsymbol{\sigma}_T^J-\boldsymbol{\sigma}_{\Delta T}^J, \\
\boldsymbol{\sigma}_2^J =&
2\Re\big\{H_\delta\boldsymbol{L}^J\boldsymbol{Z}_1^{\prime J}\boldsymbol{v}_\delta^J\big\}
+2\Re\big\{H_{-\delta}\boldsymbol{L}^J\boldsymbol{Z}_{-\delta}^{\prime J}\boldsymbol{v}_{-\delta}^J\big\} \\
\boldsymbol{u}^J =& 2\Re\big\{H_\delta\boldsymbol{A}^J\boldsymbol{Z}_\delta^J
\boldsymbol{v}_\delta^J\big\}
+2\Re\big\{H_{-\delta}\boldsymbol{A}^J\boldsymbol{Z}_{-\delta}^J
\boldsymbol{v}_{-\delta}^J\big\}
+\boldsymbol{u}_T^J-\boldsymbol{u}_{\Delta T}^J,
\end{split}
\end{equation}\end{split}\]
kde
(51)\[\begin{split}\boldsymbol{\sigma}_T^J=\left[\begin{array}{l}
T^J \\ 0
\end{array}\right],\quad
\boldsymbol{\sigma}_{\Delta T}^J=\left[\begin{array}{l}
\sigma_{\Delta Txx}^J \\ 0
\end{array}\right]\end{split}\]
(52)\[\sigma^J_{\Delta Txx}=C_{11}^J\bigg(\alpha_L^J+\frac{\nu_{LT}^J\alpha_{T'}^JE_T^J}{E_L^J}\bigg)\Delta T
+C_{12}^J\big(\alpha_T^J+\nu_{TT'}^J\alpha_{T'}^J\big)\Delta T,\]
(53)\[\boldsymbol{u}_T^J=2\Re\big\{t_1^J\boldsymbol{A}^J\boldsymbol{Z}_1^J\boldsymbol{v}_1^J\big\}
+2\Re\big\{t_2^J\boldsymbol{A}^J\boldsymbol{Z}_1^J\boldsymbol{v}_2^J\big\}\]
(54)\[\begin{split}\boldsymbol{u}_{\Delta T}^J=
\left[\begin{array}{l}
S_{11}^J\sigma_{\Delta Txx}x \\
S_{12}^J\sigma_{\Delta Txx}y
\end{array}\right].\end{split}\]
Dále platí
(55)\[\begin{split}\begin{equation}
\begin{split}
\boldsymbol{Z}_{\pm\delta}^J =&
\mathrm{diag}\Big[\big(x+\mu_1^Jy\big)^{\frac{1}{2}\pm\delta},
\big(x+\mu_2^Jy\big)^{\frac{1}{2}\pm\delta}\Big], \\
\boldsymbol{Z}_1^J =& \mathrm{diag}\Big[x+\mu_1^Jy,x+\mu_2^Jy\Big],
\end{split}
\end{equation}\end{split}\]
Hodnoty vlastních vektorů \(\boldsymbol{v}_{\pm\delta}^J\) se vyjádří z homogenní soustavy (9) a hodnoty vlastních vektorů \(\boldsymbol{v}_{1,2}^J\) jsou dány vztahy (18), (19), (20) a prvním vztahem z (12). \(T\)-napětí \(T^J\) jsou dány vztahy (31) a (37) a tenzor napětí \(\boldsymbol{\sigma}_{\Delta T}^J\) se složkou \(\sigma_{\Delta Txx}^J\) se vyjádří ze vztahu (47). Matice \(\boldsymbol{A}^J\), \(\boldsymbol{L}^J\) a \(\boldsymbol{M}^J\) jsou dány vztahy (2), (27).
Jestliže se přeznačí vektory \(\boldsymbol{\sigma}_T^J\) a \(\boldsymbol{\sigma}_{\Delta T}^J\) na tenzory
(56)\[\begin{split}\boldsymbol{\sigma}_T^J=\left[\begin{array}{ll}
T^J & 0 \\
0 & 0
\end{array}\right], \quad
\boldsymbol{\sigma}_{\Delta T}^J=\left[\begin{array}{ll}
\sigma_{\Delta Txx} & 0 \\
0 & 0
\end{array}\right],\end{split}\]
a napětí \(\boldsymbol{\sigma}_{\pm\delta}\), \(\boldsymbol{\sigma}_{t_{1,2}}\) a posuvy \(\boldsymbol{u}_{\pm\delta}\), \(\boldsymbol{u}_{t_{1,2}}\) jako části napětí a posuvů odpovídající součinitelům intenzity napětí \(H_{\pm\delta}\) a součinitelům \(t_{1,2}\), pak se součinitele intenzity napětí \(H_{\pm\delta}\) a součinitele \(t_{1,2}\) se stanoví z \(\Psi\)-integrálu podél cesty \(C\) opisující kruhovou cestu kolem vrcholu trhliny
(57)\[H_{\pm\delta}=\frac{
\int_C\Big[\big(\boldsymbol{\sigma}^{FEM}\cdot\boldsymbol{n}\big)
\cdot\hat{\boldsymbol{u}}_{\pm\delta}
-\big(\hat{\boldsymbol{\sigma}}_{\pm\delta}\cdot\boldsymbol{n}\big)
\cdot\boldsymbol{u}^{FEM}\Big]\mathrm{d}s
}{
\int_C\Big[\big(\boldsymbol{\sigma}_{\pm\delta}\cdot\boldsymbol{n}\big)
\cdot\hat{\boldsymbol{u}}_{\pm\delta}
-\big(\hat{\boldsymbol{\sigma}}_{\pm\delta}\cdot\boldsymbol{n}\big)
\cdot\boldsymbol{u}_{\pm\delta}\Big]\mathrm{d}s
}\]
(58)\[\begin{split}\begin{equation}
\begin{split}
t_{1,2} =& \frac{
\int_C\Big[\Big(\big(\boldsymbol{\sigma}^{FEM}+\boldsymbol{\sigma}_{\Delta T}\big)
\cdot\boldsymbol{n}\Big)\cdot\hat{\boldsymbol{u}}_{t_{1,2}}
}{
\int_C\Big[\big(\boldsymbol{\sigma}_{t_{1,2}}\cdot\boldsymbol{n}\big)
\cdot\hat{\boldsymbol{u}}_{t_{1,2}}
-\big(\hat{\boldsymbol{\sigma}}_{t_{1,2}}\cdot\boldsymbol{n}\big)
\cdot\boldsymbol{u}_{t_{1,2}}\Big]\mathrm{d}s
} \\
& \frac{
-\big(\hat{\boldsymbol{\sigma}}_{t_{1,2}}\cdot\boldsymbol{n}\big)
\cdot\big(\boldsymbol{u}^{FEM}+\boldsymbol{u}_{\Delta T}\big)\Big]\mathrm{d}s
}{
\int_C\Big[\big(\boldsymbol{\sigma}_{t_{1,2}}\cdot\boldsymbol{n}\big)
\cdot\hat{\boldsymbol{u}}_{t_{1,2}}
-\big(\hat{\boldsymbol{\sigma}}_{t_{1,2}}\cdot\boldsymbol{n}\big)
\cdot\boldsymbol{u}_{t_{1,2}}\Big]\mathrm{d}s
}
\end{split}
\end{equation}\end{split}\]
kde symbol \(\hat{\square}\) značí pomocné řešení.
Použité skripty
bicrack1.py - pythonovský skript pro FEniCS
bicrack1-2_gmsh.py - pythonovský skript, který vytvoří a zkompiluje soubor bicrack1-2.geo a dále vytvoří konečnoprvkovou síť bicrack1-2.msh.
bicrack_2bo.py, mod_LES_Mirek3_T.py, mod_HSV_v4.py - pythonovské skripty a nutné moduly počítající exponenty singularity napětí, součinitele intenzity napětí a \(T\)-napětí na čele trhliny u mechanického a teplotního zatížení.
GSIFs.zip - grafy, součinitele intenzity napětí a \(T\)-napětí.