Anizotropní pružnost - trhlina na rozhraní dvou monoklinických materiálů

Podobně jako v LES formalismu i v konečnoprvkovém systému FEniCS lze úspěšně využít Voigtův maticový způsob zápisu Hookeova zákona. Pro zvláštní a nejjednodušší případ anizotropních, konkrétně tzv. monoklinických, materiálů se Hookeův zákon může psát ve tvaru

(1)\[\boldsymbol{\sigma}=\boldsymbol{C}\boldsymbol{\varepsilon},\]

kde

(2)\[\begin{split}\boldsymbol{\sigma}=\left[\begin{array}{l} \sigma_{xx} \\ \sigma_{yy} \\ \sigma_{xy} \end{array}\right], \qquad \boldsymbol{\varepsilon}=\left[\begin{array}{l} \varepsilon_{xx} \\ \varepsilon_{yy} \\ 2\varepsilon_{xy} \end{array}\right],\end{split}\]

(3)\[\begin{split}\boldsymbol{C}=\boldsymbol{S}^{-1}=\left[\begin{array}{lll} 1/E_L & -\nu_{LT}/E_L & 0 \\ -\nu_{LT}/E_L & 1/E_T & 0 \\ 0 & 0 & 1/G_{LT} \end{array}\right]^{-1}.\end{split}\]

Symboly \(\sigma_{ij}\) a \(\varepsilon_{ij}\) pro \(i,j=x,y\) jsou složky tenzoru napětí a deformace a \(\boldsymbol{C}\) a \(\boldsymbol{S}\) jsou matice tuhosti a poddajnosti. Elastické konstanty \(E_L\) a \(E_T\) jsou Youngovy moduly v podélném a příčném směru vláken materiálu a \(\nu_{LT}\) Poissonova konstanta a \(G_{LT}\) modul pružnosti ve smyku v téže rovině. Výše uvedený tvar Hookeova zákona platí pro rovinnou napjatost. Pro zobecněnou rovinnou deformaci má matice tuhosti resp. poddajnosti tvar

(4)\[\begin{split}\boldsymbol{C}=\boldsymbol{S}^{-1} =\left[\begin{array}{lll} \big(1-\nu_{LT}^2E_T/E_L\big)/E_L & -\big(1+\nu_{TT}\big)\nu_{LT}/E_L & 0 \\ -\big(1+\nu_{TT}\big)\nu_{LT}/E_L & \big(1-\nu_{TT}^2\big)/E_T & 0 \\ 0 & 0 & 1/G_{LT} \end{array}\right]^{-1}.\end{split}\]

Zbývá formulovat slabou formu úlohy, která se může při zanedbání objemových sil zapsat následovně,

(5)\[\int_\Omega\boldsymbol{\sigma}:\delta\boldsymbol{\varepsilon}\mathrm{d}\Omega -\int_{\partial\Omega}\boldsymbol{t}\cdot\delta\boldsymbol{u}\mathrm{d}\partial\Omega=0,\]

kde

(6)\[\boldsymbol{t}=\boldsymbol{\sigma}\cdot\boldsymbol{n}\]

je vektor napětí, \(\boldsymbol{n}\) je vnější normála k hranici \(\delta\Omega\) a \(\boldsymbol{u}\) jsou posuvy, pro které platí

(7)\[\boldsymbol{\varepsilon}=\frac{1}{2}(\nabla\boldsymbol{u}+\boldsymbol{u}\nabla).\]

Formulace úlohy

Uvažujme dvourozměrnou oblast \(\Omega\) složenou za dvou monoklinických materiálů. Rozhraní obou materiálů leží podél osy \(x\), přičemž podél její záporné části se nachází trhlina. Geometrie, uložení, vnější zatížení a poloha vzhledem k počátku souřadnicového systému jsou na následujícím obrázku.

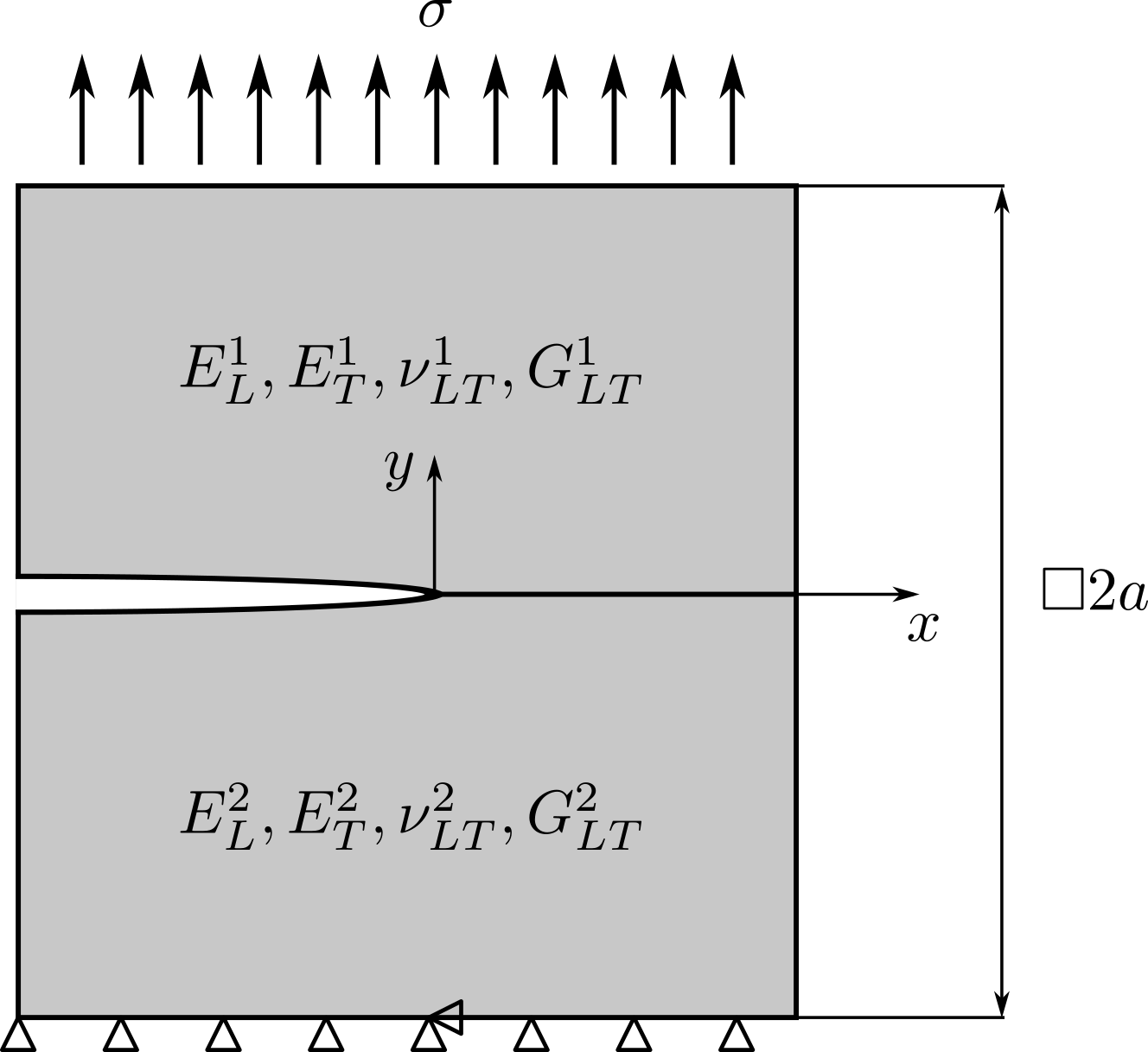
Předpokládejme, že rozměry, elastické konstanty obou materiálů a hodnoty zatížení jsou následující

(8)\[a=90\,\mathrm{mm}\qquad\sigma=100\,\mathrm{MPa}\]

(9)\[\begin{split}\begin{equation} \begin{split} & E_L^1=0.10\times 10^{12}\,\mathrm{Pa} \\ & E_T^1=0.50\times 10^{11}\,\mathrm{Pa} \\ & \nu_{LT}^1=0.3 \\ & G_{LT}^1=0.30\times 10^{11}\,\mathrm{Pa} \\ & \\ & E_L^2=0.40\times 10^{12}\,\mathrm{Pa} \\ & E_T^2=0.50\times 10^{11}\,\mathrm{Pa} \\ & \nu_{LT}^2=0.3 \\ & G_{LT}^2=0.30\times 10^{11}\,\mathrm{Pa} \\ \end{split} \end{equation}\end{split}\]

Použité skripty

Konečnoprvkové skripty jsou platné pro FEniCS v2018.1.0.

• bicrack0.py - pythonovský skript pro FEniCS
• bicrack0_gmsh.py - pythonovský skript, který vytvoří a zkompiluje soubor bicrack0.geo a dále vytvoří konečnoprvkovou síť bicrack0.msh.
• ANSYS_mat1_raw_data_180_90.dat, ANSYS_mat2_raw_data_180_90.dat - data z ANSYSu.
• LES_Mirek0.py, mod_HSV_v4.py, mod_plot_fcn.py - pythonovský skript a nutné moduly počítající exponenty singularity napětí a součinitele intenzity napětí na čele trhliny.

Numerické výsledky

Nejdříve ukázka konečnoprvkové sítě v celku a detailu kořene trhliny (kliknutím se obrázky zvětší).

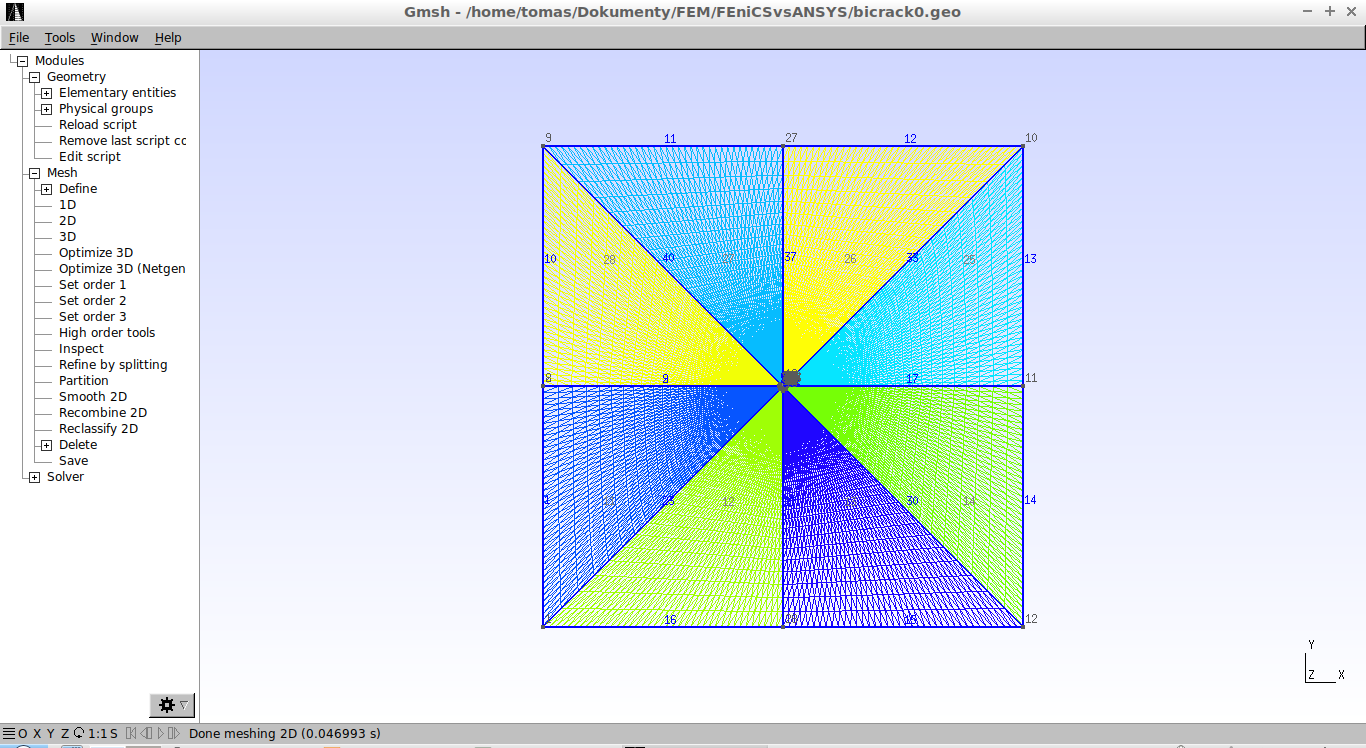
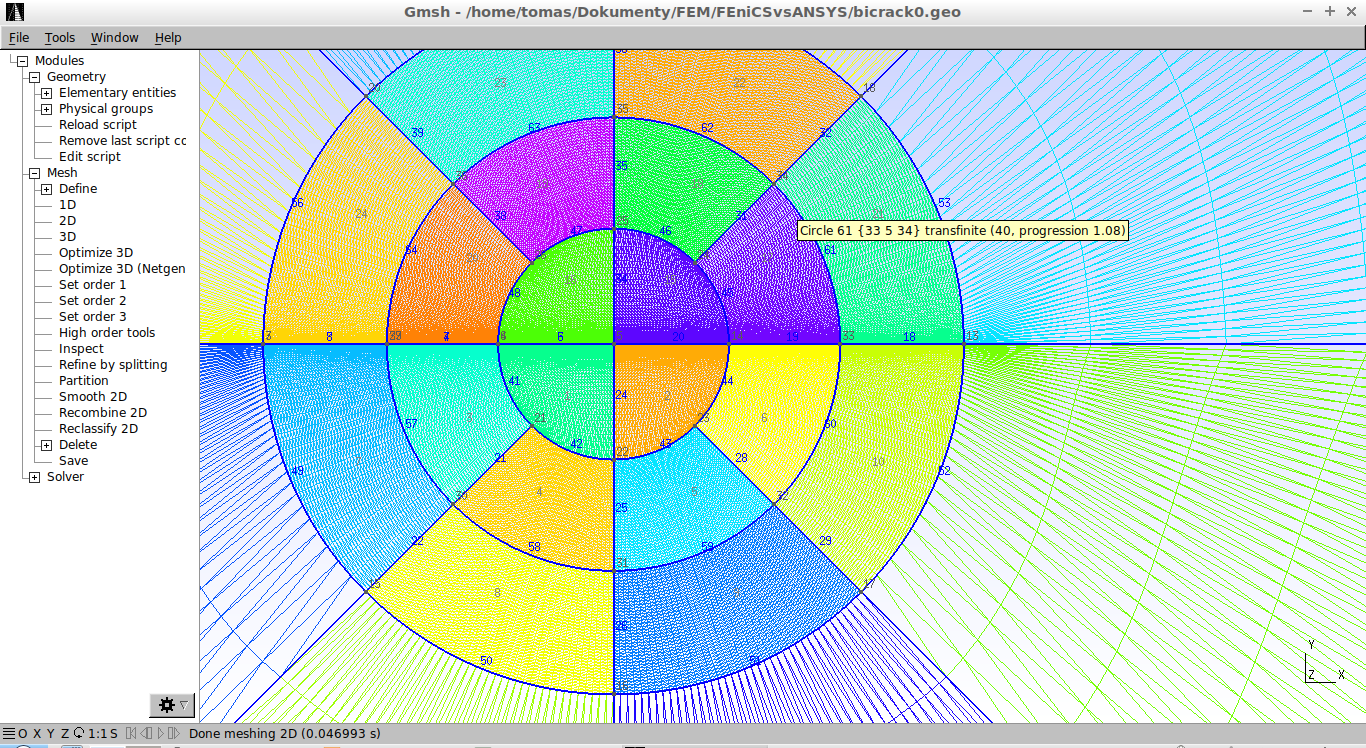
Výsledkem jsou následující roztomilé barevné obrázky, které přes svou nulovou informační hodnotu dávají alespoň představu o deformaci tělesa a rozložení napětí v okolí kořene trhliny ve tvaru "motýla" (kliknutím se obrázky zvětší).

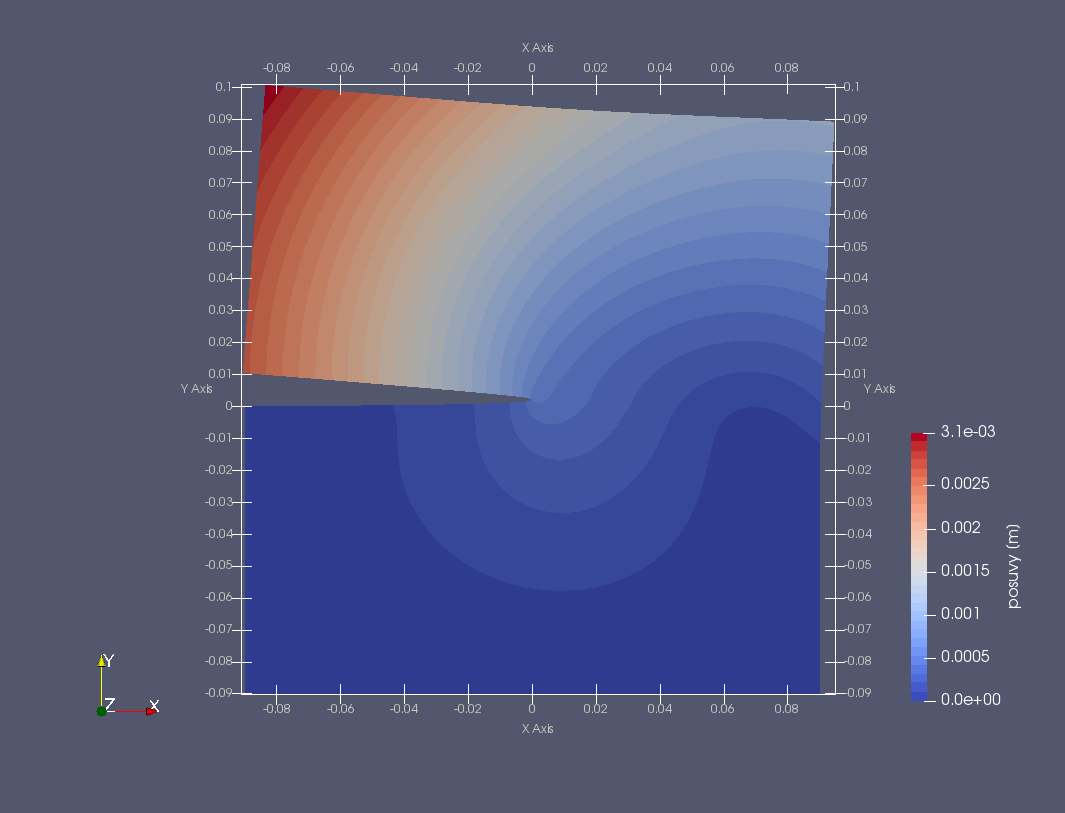
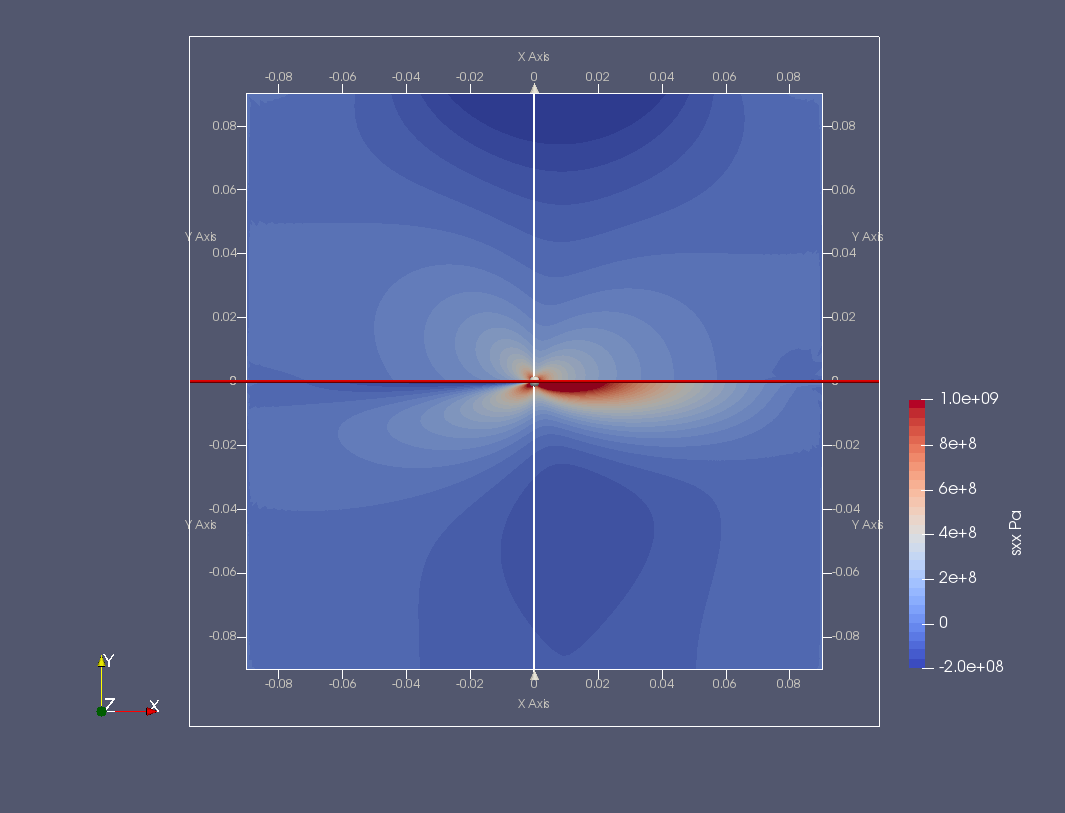
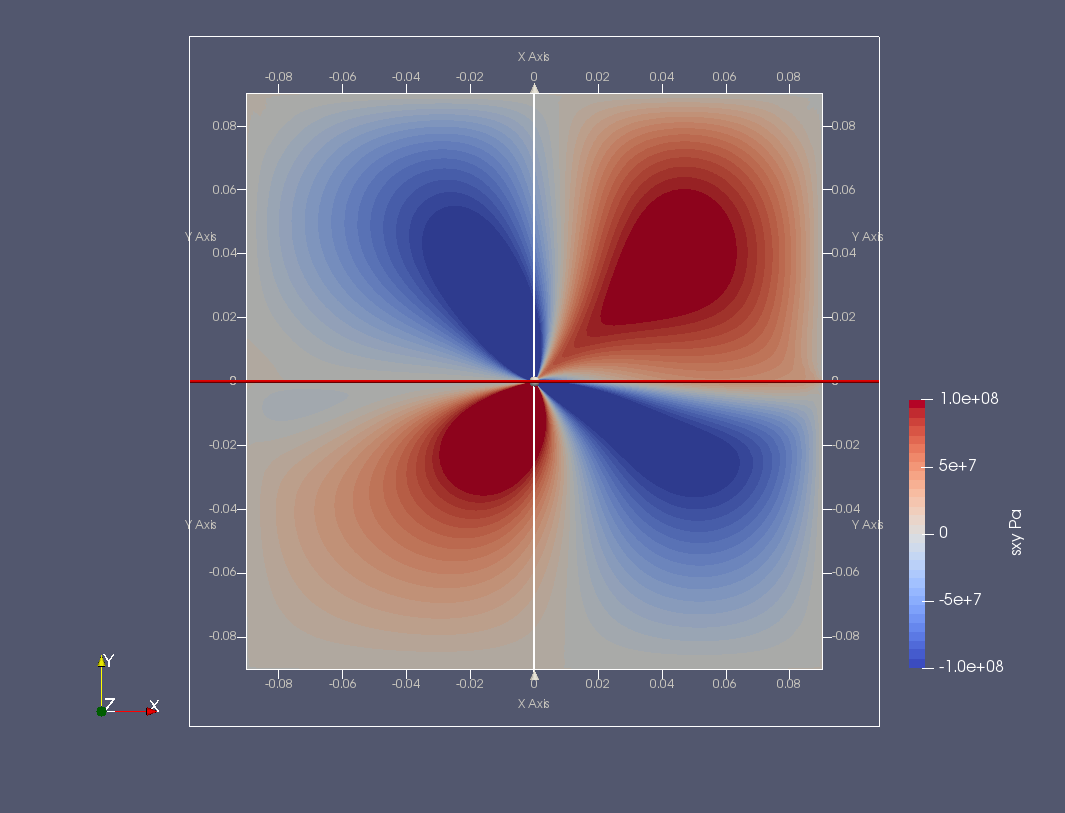
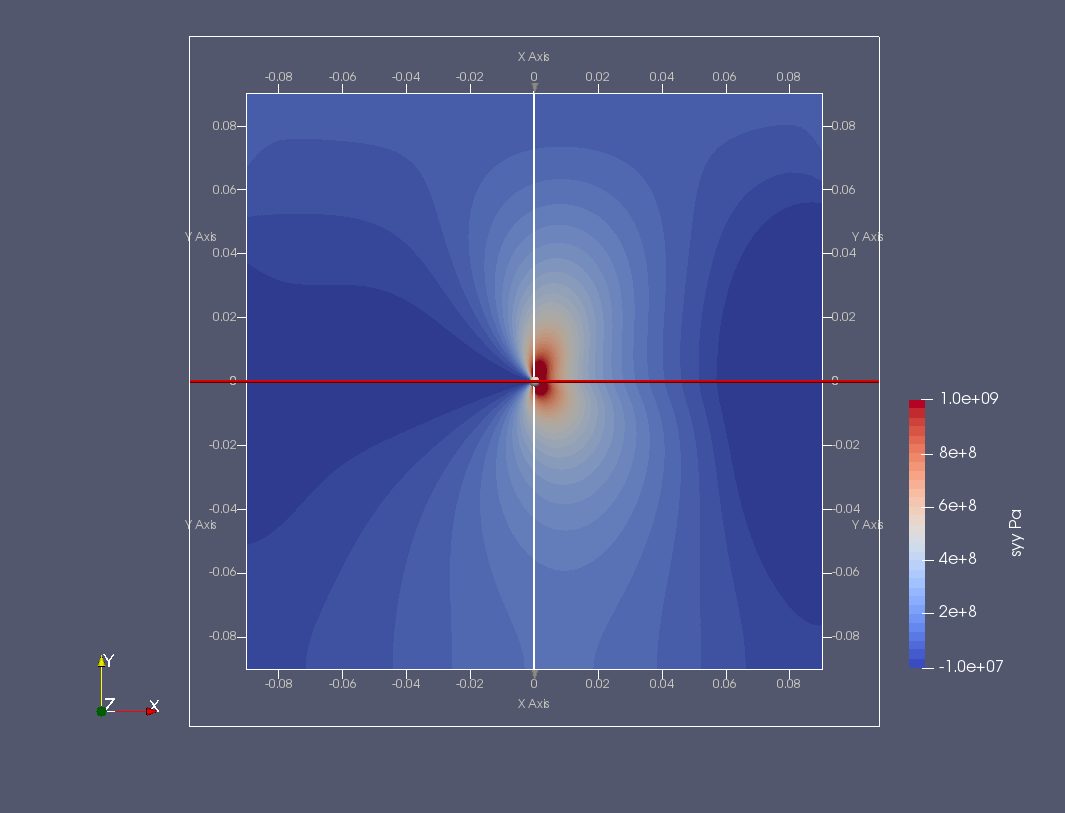
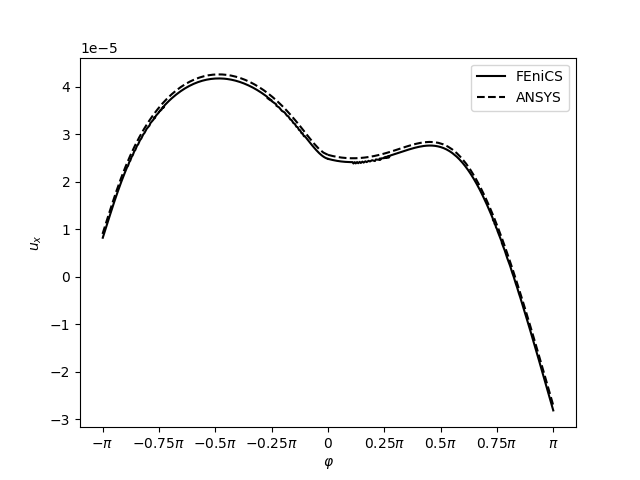
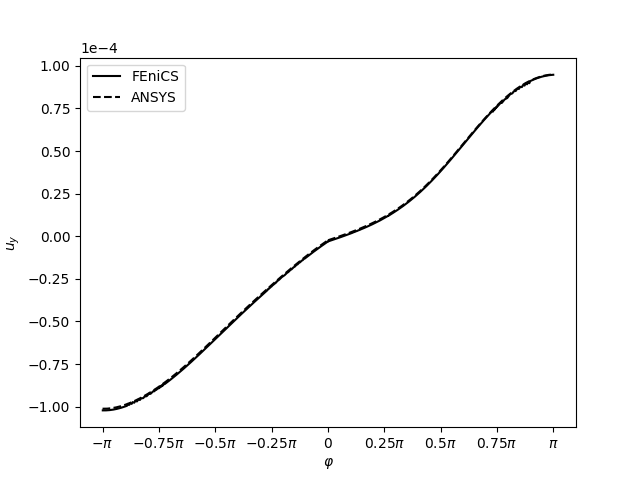
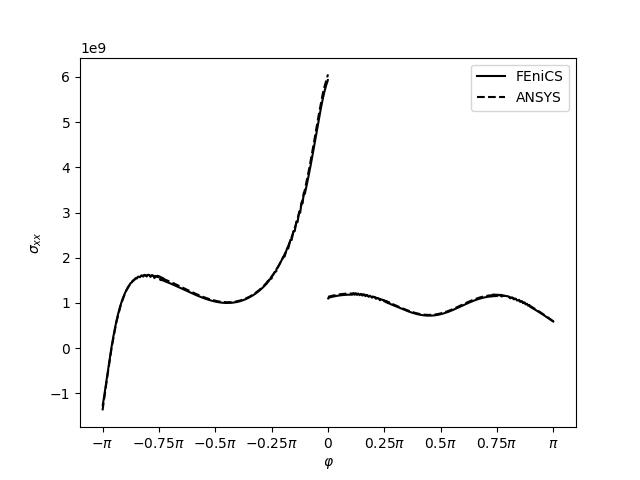
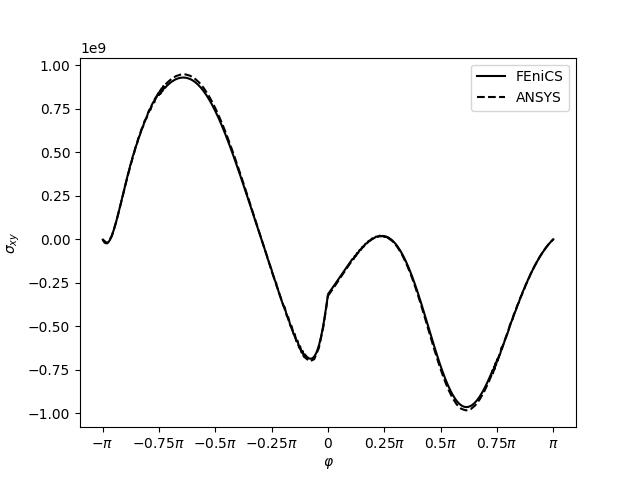
Zajímavější je srovnání výsledků získaných z FEniCSu a komerčního ANSYSu. Toto srovnání se již musí provést konkrétně, např. podél kruhové cesty kolem vrcholu trhliny na poloměru \(R_{path}=0.011a=0.001\,\mathrm{m}\), jak ukazují následující grafy (kliknutím se obrázky zvětší).