Gradietní pružnost - slabá formulace

Následující příklad demonstruje použití FEniCSu v2017.2.0 v oblasti gradientní pružnosti. Většinou se v následujících vztazích využívá sčítací Einsteinova konvence, pokud to není uvedeno jinak. I když uvedené vztahy platí pro 3D, úlohy zde řešené jsou pouze 2D.

Základní vztahy

Toupin [1] a Mindlin [2] dali do kupy lineární pružnost, ve které deformační energie nezávisí nejen na deformaci

(1)\[\varepsilon_{ij} = \frac{1}{2}\big(\partial_j u_i+\partial_i u_j\big),\]

ale také na jejím gradientu,

(2)\[\eta_{ijk} = \partial_i\partial_j u_k.\]

Zde \(\boldsymbol{u}\) je vektor posuvů a dále samozřejmě platí \(\varepsilon_{ij}=\varepsilon_{ji}\) a \(\eta_{ijk}=\eta_{jik}\). Dodatečně se musí ke Cauchyovu napětí \(\sigma_{ij}\) zavést napětí vyššího řádu \(\tau_{ijk}=\tau_{jik}\) jako konjugovaná veličina ke gradientu deformace \(\eta_{ijk}\). Tyto veličiny musí být ve statické rovnováze, která je daná vztahy,

(3)\[b_k+\partial_i\big(\sigma_{ik}-\partial_j\tau_{jik}\big)=0,\]

(4)\[f_k=n_i\big(\sigma_{ik}-\partial_j\tau_{jik}\big)+n_i n_j\tau_{ijk}\big(D_p n_p\big) -D_j\big(n_i\tau_{ijk}\big),\]

(5)\[r_k=n_i n_j \tau_{ijk},\]

kde \(\boldsymbol{b}\) je objemová síla, \(\boldsymbol{f}\) a \(\boldsymbol{r}\) je vektor napětí a vektor "dvojitých" napětí na hranici \(\partial\Omega\) a \(\boldsymbol{n}\) je vnější normála hranice \(\partial\Omega\). Pro operátor povrchového gradientu \(D_j u_k\) platí

(6)\[D_j u_k=\big(\delta_{jl}-n_j n_l\big)\partial_l u_k\]

přičemž se v dalším bude potřebovat i operátor povrchového normálového gradientu,

(7)\[D u_k=n_l\partial_l u_k.\]

Zbývá uvést konstitutivní vztahy. V případě gradientní pružnosti má hustota potenciální energie tvar,

(8)\[\begin{split} \begin{equation} \begin{split} w =& \frac{1}{2}\lambda\varepsilon_{ll}\varepsilon_{ll}+\mu\varepsilon_{ij}\varepsilon_{ij} \\ & + l^2\frac{1}{2}\lambda\partial_k\varepsilon_{ll}\partial_k\varepsilon_{ll} + l^2\mu\partial_k\varepsilon_{ij}\partial_k\varepsilon_{ij}, \end{split} \end{equation}\end{split}\]

kde \(\lambda\) a \(\mu\) jsou Lamého konstanty a \(l^2\) je gradientní koeficient s rozměry \([délka]^2\). Cauchyho napětí \(\sigma_{ij}\) a výše zmíněná "dvojitá" napětí \(\tau_{ijk}\) se pak vyjádří následovně,

(9)\[\begin{split}\begin{equation} \begin{split} \sigma_{ij} =& \frac{\partial w}{\partial\varepsilon_{ij}}=\lambda\delta_{ij}\varepsilon_{ll} +2\mu\varepsilon_{ij}, \\ \tau_{ijk} =& \frac{\partial w}{\partial\eta_{ijk}}=l^2\partial_i\big(\lambda\delta_{jk}\varepsilon_{ll} +2\mu\varepsilon_{jk}\big). \end{split} \end{equation}\end{split}\]

Gradientní teorie pro jednoznačné řešení vyžaduje v případě rovinné úlohy čtyři nezávislé okrajové podmínky. Jsou to předpisy hodnot na hranici pro \(\boldsymbol{f}\) nebo \(\boldsymbol{u}\) a \(\boldsymbol{r}\) nebo vektor

(10)\[\big(Du_1,Du_2).\]

Je zřejmé, že okrajové podmínky pro \(\boldsymbol{r}\) a (10) jsou pro gradientní pružnost specifické. Ze vztahů (2), (3) a (9) plyne, že bázové funkce nad prvky metody konečných prvků (MKP) musí mít spojité první derivace, tj. musí být z množiny funkcí \(C^1\). Pro dvourozměrné a třírozměrné úlohy nejsou takové prvky s rozumným chováním v MKP k dispozici. Tento problém se obchází kombinací více prostorů bázových funkcí z množiny spojitých funkcí \(C^0\) zvoleného prvku, jak je ukázáno v [3]. Na rozdíl od řady MKP softwarů, FEniCS vlastnost kombinace různých prostorů funkcí definovaných na prvku bravurně zvládá. K tomu je ale nejdříve nutné formulovat odpovídající slabou formulaci problému. Za předpokladu platnosti rovnic rovnováhy (3)-(5) se zavede tenzor druhého řádu \(\boldsymbol{\psi}\), který se sváže s gradientem deformace, tj. tenzorem třetího řádu, následovně

(11)\[\hat{\eta}_{ijk}\equiv\frac{1}{2}\big(\partial_i\psi_{jk}+\partial_j\psi_{ik}\big).\]

Pak se slabá formulace rovnic rovnováhy (3)-(5) může z principu virtuálních prací a po aplikaci Stokesovy věty psát ve tvaru,

(12)\[\begin{split}\begin{equation} \begin{split} &\int_{\Omega}\big[\boldsymbol{\sigma}:\delta\boldsymbol{\varepsilon} +\boldsymbol{\tau}:\cdotp\delta\boldsymbol{\hat{\eta}} +(\nabla\cdot\boldsymbol{\tau})\colon\big(\delta\boldsymbol{\psi} -\nabla\delta\boldsymbol{u}\big)\big]\mathrm{d}\Omega \\ =& \int_{\Omega}\boldsymbol{b}\cdotp\delta\boldsymbol{u}\mathrm{d}\Omega +\int_{\partial\Omega}\big[\boldsymbol{f}\cdotp\delta\boldsymbol{u} +\boldsymbol{nr}\colon\delta\boldsymbol{\psi}\big]\mathrm{d}\partial\Omega \\ & +\int_{\partial\Omega}(\boldsymbol{n}\cdot\boldsymbol{\tau}-\boldsymbol{n}\boldsymbol{r}) \colon\big(\delta\boldsymbol{\psi}-\nabla\delta\boldsymbol{u}\big)\mathrm{d}\partial\Omega \end{split} \end{equation}\end{split}\]

pro libovolnou variaci \(\delta\boldsymbol{u}\) a \(\delta\boldsymbol{\psi}\). Jestliže bude \(\boldsymbol{\psi}\) vyhovovat své klasické definici, tj.

(13)\[\boldsymbol{\psi}=\nabla\boldsymbol{u},\]

pak \(\boldsymbol{\hat{\eta}}\) bude totožné s (2). Bohužel v případě MKP tyto striktní rovnosti není možné dodržet, protože by to vedlo na řešení s nutností spojitosti \(C^1\) bázových funkcí na prvku. Pro udržení pouze \(C^0\) spojitosti bázových funkcí je proto nutné striktní rovnost (13) oslabit ve smyslu vážených reziduí,

(14)\[\int_{\Omega}\big(\psi_{jk}-\partial_j u_k\big)\delta\partial_i\tau_{ijk}\mathrm{d}\Omega=0 \qquad (\mathrm{nesčítá}\,\mathrm{se}\,\mathrm{přes}\,j\,\mathrm{a}\,k)\]

pro libovolnou hodnotu Lagrangeova multiplikátoru \(\delta\partial_i\tau_{ijk}=\partial_i\delta\tau_{ijk}\). Vztah (14) zajistí, že se poslední člen v (12) může zanedbat a přeznačením Lagrangeových multiplikátorů na

(15)\[\boldsymbol{\rho}=\nabla\cdot\boldsymbol{\tau}\]

se slabá formulace (12) může psát ve tvaru,

(16)\[\begin{split}\begin{equation} \begin{split} &\int_{\Omega}\big[\boldsymbol{\sigma}:\delta\boldsymbol{\varepsilon} +\boldsymbol{\tau}:\cdotp\delta\boldsymbol{\hat{\eta}} +\boldsymbol{\rho}:\big(\delta\boldsymbol{\psi} -\nabla\delta\boldsymbol{u}\big)\big]\mathrm{d}\Omega \\ &\thickapprox \int_{\Omega}\boldsymbol{b}\cdotp\delta\boldsymbol{u}\mathrm{d}\Omega +\int_{\partial\Omega}\big[\boldsymbol{f}\cdotp\delta\boldsymbol{u} +\boldsymbol{\tilde{r}}\colon\delta\boldsymbol{\psi}\big]\mathrm{d}\partial\Omega, \end{split} \end{equation}\end{split}\]

kde \(\boldsymbol{\tilde{r}}=\boldsymbol{nr}\) a

(17)\[\int_{\Omega}\big(\psi_{jk}-\partial_j u_k\big)\delta\rho_{jk}\mathrm{d}\Omega=0 \qquad (\mathrm{nesčítá}\,\mathrm{se}\,\mathrm{přes}\,j\,\mathrm{a}\,k).\]

Aby nedocházelo k záměně, nazývá se \(\boldsymbol{\psi}\) jako relaxovaný gradient posuvů na rozdíl od skutečného gradientu (13) a podobně

(18)\[\boldsymbol{\hat{\varepsilon}} = \frac{1}{2}\big(\boldsymbol{\psi}+\boldsymbol{\psi}^T\big)\]

se nazývá jako relaxovaná deformace na rozdíl od skutečné deformace (1). Technika Lagrangeových multiplikátorů (14) zajišťuje, že \(\boldsymbol{\psi}\) vhodně aproximuje \(\nabla\boldsymbol{u}\) a (18) vhodně aproximuje skutečné \(\boldsymbol{\varepsilon}\). Zbývá poznámka k okrajovým podmínkám. Jak již bylo zmíněno výše, v případě rovinné úlohy je nutné sestavit čtyři okrajové podmínky. Jestliže hodnoty na hranici jsou označeny s indexem \(*\), nejjednodušší okrajové podmínky jsou předepsané hodnoty vektoru napětí \(\boldsymbol{f^*}\) a vektor dvojitých napětí \(\boldsymbol{r^*}\), tj. platí,

(19)\[\boldsymbol{f}=\boldsymbol{f^*}\quad\mathrm{a}\quad\boldsymbol{\tilde{r}}=\boldsymbol{nr^*}.\]

V případě předepsaných posuvů \(\boldsymbol{u^*}\) a jejich gradientů \(D\boldsymbol{u^*}\) je situace trošku komplikovanější. Jestliže \(\boldsymbol{t}\) značí tečnu kolmé k normále \(\boldsymbol{n}\) v bodě hranice, pak platí,

(20)\[\boldsymbol{u}=\boldsymbol{u^*}\quad\mathrm{a}\quad\boldsymbol{\psi}=\boldsymbol{n}D\boldsymbol{u^*} +\boldsymbol{t}D_t\boldsymbol{u^*},\]

kde

(21)\[D_t\boldsymbol{u^*}=\boldsymbol{t}\cdot\nabla\boldsymbol{u^*}.\]

Formulace problému

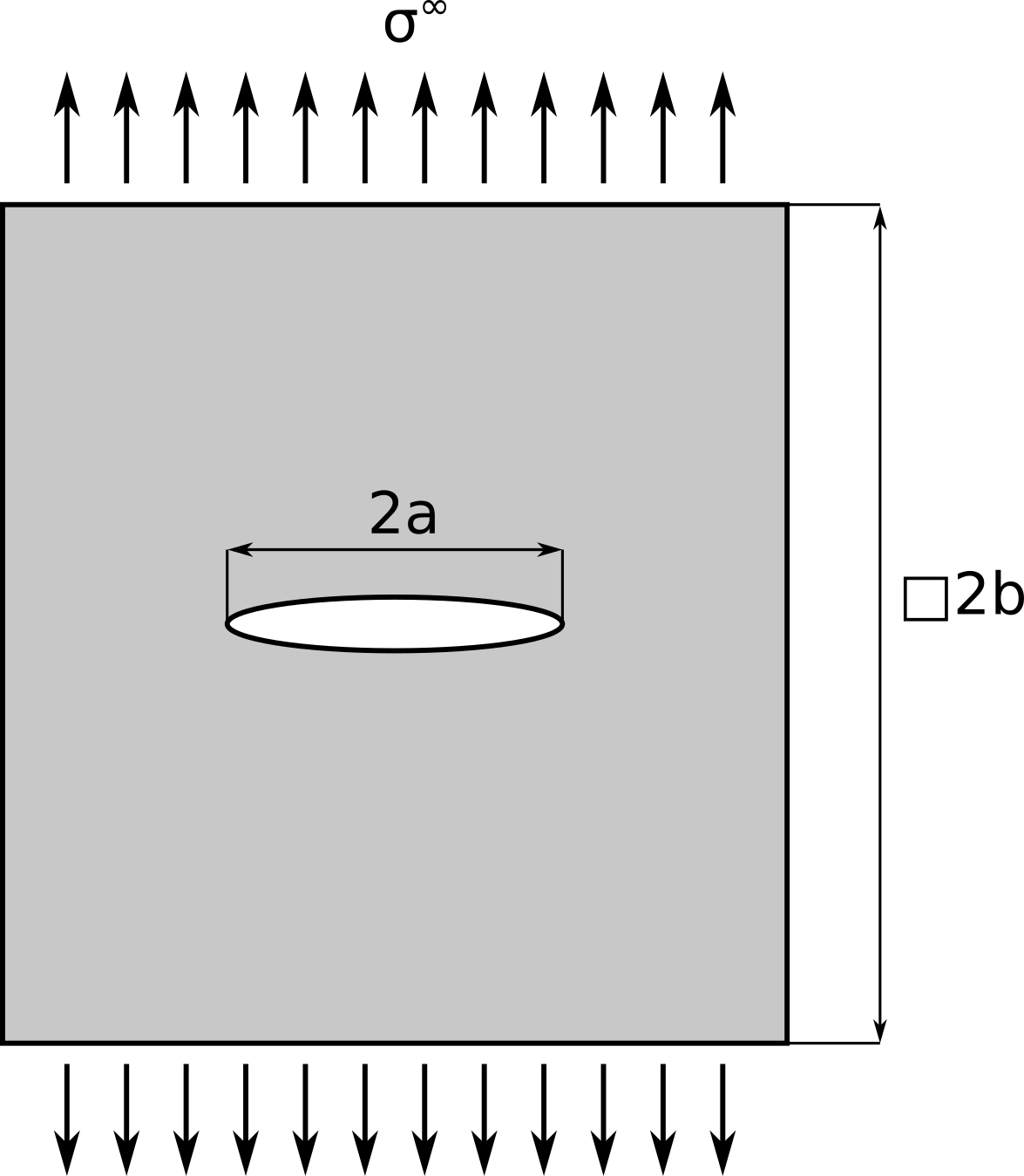
Následující ukázka je řešení případu trhliny délky \(2a\) v homogenním materiálu o rozměrech \(2b\times 2b\) a zatíženého na horní a dolní hraně normálovým napětím \(\sigma^\infty\). Materiál je charakterizován elastickými konstantami \(E\), \(\nu\) a délkovým parametrem \(l\).

Implementace

Nápovědu pro implementaci ve FEniCSu lze nalézt v [4]. Nicméně FEniCS je stále ve vývoji a zápis použitých příkazů se mění. Takže i kód v [4] je překonaný a za chvíli bude i ten níže uvedený.

Prvním krokem je vytvoření konečnoprvkové sítě pomocí programu GMSH. Velice jednoduchý skript pro GMSH je níže. Využívá symetrie úlohy tak, že modeluje pouze pravou horní čtvrtinu oblasti, kde hrany 1 a 4 jsou na osách symetrie. Trhlina je reprezentována hranou 5. Rozměry jsou \(a=0.1\,\mathrm{mm}\) a \(b=1.0\,\mathrm{mm}\).

cl__1 = 1;

Point(1) = {0, 0, 0, 0.001};
Point(2) = {1, 0, 0, 0.1};
Point(3) = {1, 1, 0, 0.1};
Point(4) = {0, 1, 0, 0.1};
Point(5) = {0.1, 0, 0, 0.001};

Line(1) = {1, 4};
Line(2) = {4, 3};
Line(3) = {3, 2};
Line(4) = {2, 5};
Line(5) = {5, 1};

Line Loop(1) = {1, 2, 3, 4, 5};
Plane Surface(1) = {1};

Physical Line(1) = {1};
Physical Line(2) = {2};
Physical Line(3) = {3};
Physical Line(4) = {4};
Physical Line(5) = {5};
Physical Surface(0) = {1};

Výsledek skriptu je následující (kliknutím se obrázek zvětší).

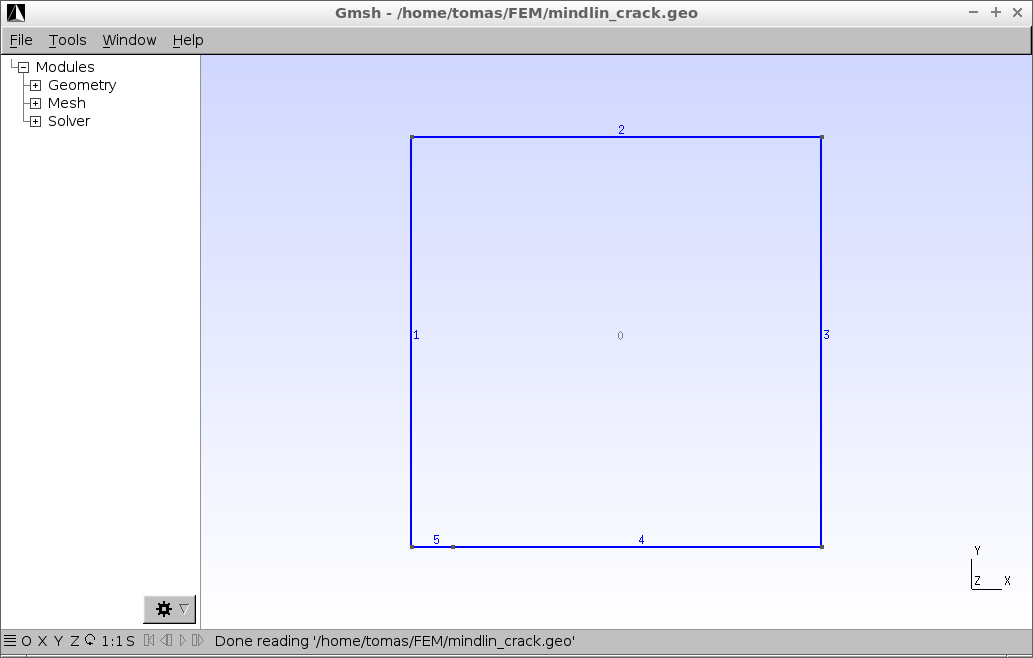
Cílem je získat popis deformace a napětí v nejbližším okolí trhliny, proto je síť hustá v místě trhliny. Hustota sítě se ovlivňuje čtvrtým parametrem příkazu Point. Čím menší číslo, tím jemnější síť v okolí daného bodu. V tomto případě jsou to body 1 a 5, které jsou body největšího rozevření trhliny a jejího čela.

Samozřejmě, podstatné je fyzické očíslování hranice oblasti a jejího vnitřku, které se provádí na posledních šesti řádcích výše uvedeného skriptu příkazy Physical Line a Physical Surface. Oblast má index 0, líc trhliny má index 5. Hranice podél svislé osy symetrie má index 1, podél vodorovné osy symetrie má index 4. Konečně horní a pravá hranice mají indexy 2 a 3. Po vygenerování sítě příkazem Mesh > 2D se dostane následující výsledek (kliknutím se obrázek zvětší).

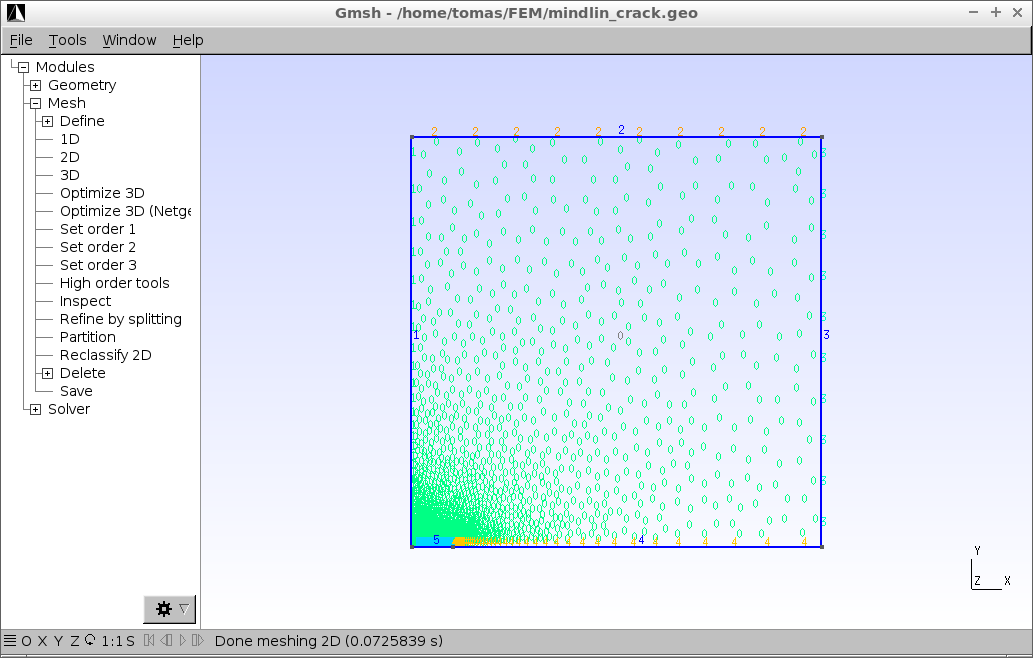
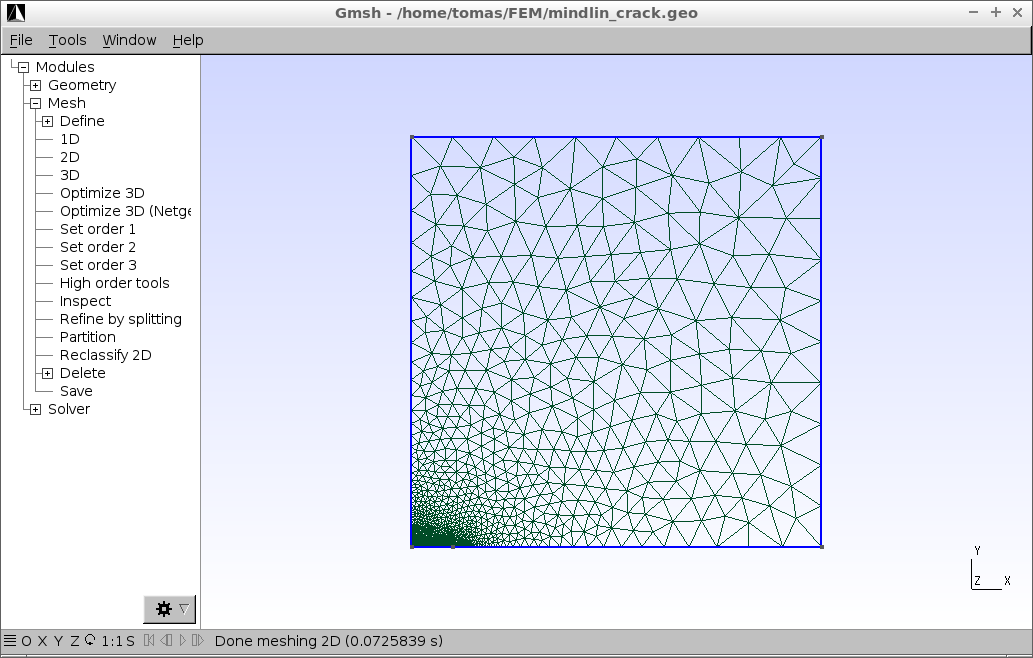
Po uložení Mesh > Save do souboru mindlin_crack.msh je nutné síť ještě udělat dostupnou pro FEniCS. K tomu se použije již výše zmíněný program dolfin-convert,

uživatel$ dolfin-convert soubor.msh soubor.xml

Program dolfin-convert vytvoří v tomto případě pouze dva xml soubory. Soubor mindlin_crack.xml, který poskytuje celkové informace o konečnoprvkové síti a soubor mindlin_crack_facet_region.xml, který obsahuje informace o indexech hranice. Protože konečnoprvková síť neobsahuje žádné podoblasti, soubor s informací o podoblastech nebyl vygenerován a FEniCS ji difóltně přiřadí index 0, pokud nedostane pokyn tento index změnit (a proč by taky měl, že ano?). Import konečnoprvkové sítě se provede následovně.

from dolfin import *

mesh=Mesh("mindlin_crack.xml")
boundaries=MeshFunction("size_t",mesh,"mindlin_crack_facet_region.xml")

V dalším kroku se musí nad prvky sítě vygenerovat vhodné prostory funkcí. Vektor posuvů \(\boldsymbol{u}\) se bude aproximovat Lagrangeovými polynomy 2. stupně, těm odpovídá symbol CG. Tenzor relaxovaného gradientu posuvů \(\boldsymbol{\psi}\) se bude aproximovat taktéž Lagrangeovými polynomy, ale pouze 1. stupně. A konečně Lagrangeovy multiplikátory se budou aproximovat nespojitými konstantami (polynomy 0. stupně), kterým odpovídá symbol DG. Jednotlivé prostory se smíchají příkazem FunctionSpace a MixedElement.

V=VectorElement("CG",mesh.ufl_cell(),2)
VV=TensorElement("CG",mesh.ufl_cell(),1)
VVV=TensorElement("DG",mesh.ufl_cell(),0)

MX=FunctionSpace(mesh,MixedElement([V,VV,VVV]))

Samotná slabá řešení a testovací funkce na smíchaném prostoru funkcí se označí jako u a w pro posuvy, jako u_RStrain a w_RStrain pro relaxované gradienty posuvů a u_Lagrange a w_Lagrange pro Lagrangeovy multiplikátory.

(u,u_RStrain,u_Lagrange)=TrialFunctions(MX)
(w,w_RStrain,w_Lagrange)=TestFunctions(MX)

Fundamentální záležitostí je sestavení okrajových podmínek. Nejdříve podél svislé osy symetrie, tj. hranice 1:

1. Osa symetrie se neposouvá ve směru osy \(x\) platí \(u_x=0\).

2. Na ose symetrie nejsou smyková napětí, tj. \(f_y=0\).

Protože jsou podle bodu 1 posuvy \(u_x\) konstantní (nulové) podél osy \(y\), musí platit \(\partial_y u_x=0\). Protože jsou dále podle bodu 2 smyková napětí nulová, jsou i odpovídající deformace nulové, tj. \(\partial_x u_y+\partial_y u_x=0\). Odtud plyne, že také \(\partial_x u_y=0\). Pro relaxované gradienty posuvů pak platí,

(22)\[\begin{split}\begin{bmatrix} \psi_{11} & \psi_{12} \\ \psi_{21} & \psi_{22} \end{bmatrix} = \begin{bmatrix} \partial_x u_x & \partial_x u_y \\ \partial_y u_x & \partial_y u_y \end{bmatrix} = \begin{bmatrix} \partial_x u_x & 0 \\ 0 & \partial_y u_y \end{bmatrix}\end{split}\]

Odtud plynou podmínky pro relaxované gradienty posuvů,

3. \(\psi_{xy}=0\).

4. \(\psi_{yx}=0\).

Okrajové podmínky podél horní hranice 2:

1. Smyková napětí nejsou zadána, tj. \(f_x=0\).

2. Normálová napětí naopak zadána jsou, tj. \(f_y=\sigma^\infty\).

3. Zbývá zadat podmínky výšších "forem" - žádné gradientní napětí není zadáno, takže \(r_x=0\).

4. Stejně tak \(r_y=0\).

Okrajové podmínky podél pravé hranice 3:

1. Smyková napětí nejsou zadána, tj. \(f_y=0\).

2. Normálová napětí tentokrát také ne, tj. \(f_x=0\).

3. Taktéž gradientní napětí není zadáno, takže \(r_x=0\).

4. A stejně tak \(r_y=0\).

Okrajové podmínky podél vodorovné osy symetrie, tj. hranice 4:

1. Osa symetrie se neposouvá ve směru osy \(y\), tj. \(u_y=0\).

2. Na ose symetrie nejsou smyková napětí, tj. \(f_x=0\).

3. Podobně jako u hranice 1 pro relaxované gradienty posuvů platí \(\psi_{xy}=0\)

4. a \(\psi_{yx}=0\).

Zbývá tyto okrajové podmínky formulovat ve FEniCSu. Nejdříve třeba vektory napětí \(\boldsymbol{f}\), konkrétně vektor napětí na horní hranici 2, protože zbývající jsou nulové a můžou se nechat plavat, jelikož se ve formulaci virtuální práce neobjeví. Jak již bylo zmíněno v předchozích příkladech je několik způsobů, jak zadat algebraický výraz do DOLFINu. Např. pomocí třídy Expression. Novinka jejího použití zde, a na rozdíl od Poissonovy úlohy uvedené výše, je metoda value_shape, která zvyšuje dimenzi výrazu Expression.

class tractions2(Expression):
  def eval(self,value,x):
    value[0]=0.
    value[1]=1.e2 #MPa
  def value_shape(self):
    return (2,)

Gradienty vektoru napětí \(\boldsymbol{r}\) není třeba formulovat, protože jsou pro změnu na všech částech hranice oblasti nulové nebo neznámé. Zbývají Dirichletovy podmínky pro \(\boldsymbol{u}\) a \(\boldsymbol{\psi}\). První se formulují jako vektor příkazem DirichletBC. V tomto případě posuvy \(u_x\) a \(u_y\) jsou součástí vektorového prostoru V a vyjádří se jako MX.sub(0).sub(0) a MX.sub(0).sub(1). Relaxované gradienty posuvů \(\psi_{xy}\) a \(\psi_{yx}\) jsou součástí tenzorového prostoru funkcí VV, tj. prostoru funkcí MX.sub(1) a jsou to druhá a třetí složka tohoto podprostoru, tj. MX.sub(1).sub(1) a MX.sub(1).sub(2). Definice Dirichletových podmínek může vypadat následovně,

null=Constant(0.0)

bcs=[DirichletBC(MX.sub(0).sub(0),null,boundaries,1),
     DirichletBC(MX.sub(0).sub(1),null,boundaries,4),
     DirichletBC(MX.sub(1).sub(1),null,boundaries,1),
     DirichletBC(MX.sub(1).sub(2),null,boundaries,1),
     DirichletBC(MX.sub(1).sub(1),null,boundaries,4),
     DirichletBC(MX.sub(1).sub(2),null,boundaries,4)]

V dalším budou potřeba elastické charakteristiky materiálu \(E\), \(\nu\), \(\lambda\), \(\mu\) a \(l\).

E=2.1e5 #MPa
nu=0.25
Lambda=E*nu/(1.-nu*nu) #Plane stress
G=E/(2.*(1.+nu))
mu=G
nonloc=0.01 #mm

Jednotková matice reprezentující Dirackovu \(\delta\)-funkci a zavední indexů i, j, k a l (difóltně jsou ve FEniCSu zavedeny jen první tři) se provede následovně.

delta=Identity(mesh.ufl_cell().geometric_dimension())
i,j,k,l=indices(4)

Dříve než se definuje slabá formulace úlohy, zavedou se tenzorové veličiny, které závisí na \(\boldsymbol{u}\) a \(\boldsymbol{\psi}\).

(23)\[\begin{split}\begin{equation} \begin{split} \varepsilon_{ij} =& \frac{1}{2}\big(\partial_j u_i+\partial_i u_j\big), \\ \sigma_{ij} =& \lambda\delta_{ij}\partial_k u_k+\mu\big(\partial_j u_i+\partial_i u_j\big), \\ \hat{\eta}_{ijk} =& \frac{1}{2}\big(\partial_i\psi_{jk}+\partial_j\psi_{ik}\big), \\ \tau_{ijk} =& l^2\big[\lambda\delta_{jk}\partial_i\psi_{ll}+\mu\big(\partial_i\psi_{jk} +\partial_i\psi_{kj}\big)\big]. \end{split} \end{equation}\end{split}\]

Ve FEniCSu se tyto vztahy mohou definovat klasickou pythonovskou procedurou def

def StrainT(u):
  return as_tensor((1./2.*(u[i].dx(j)+u[j].dx(i))),[i,j])

def StressT(u):
  return as_tensor((Lambda*StrainT(u)[k,k]*delta[i,j]+2*mu*StrainT(u)[i,j]),[i,j])

def RStrainGrad(u_RStrain):
  return as_tensor((1./2.*(u_RStrain[j,k].dx(i)+u_RStrain[i,k].dx(j))),[i,j,k])

def HStress(u_RStrain):
  return as_tensor(nonloc*nonloc*(Lambda*u_RStrain[l,l].dx(i)*delta[j,k]
                    +mu*(u_RStrain[j,k].dx(i)+u_RStrain[k,j].dx(i))),[i,j,k])

Zbývá sestavit slabou formulaci úlohy, kde je cílem nalézt takové \(\boldsymbol{u}\in V_{2}\), \(\boldsymbol{\psi^u}\in V_{2\times 2}\) a \(\boldsymbol{\rho^u}\in W_{2\times 2}\) a kde \(V_2\), \(V_{2\times 2}\) a \(W_{2\times 2}\) je vektorový prostor, tenzorový a opět tenzorový prostor funkcí dostatečně hladkých tak, že

(24)\[\begin{equation} \begin{split} a\big((\boldsymbol{u},\boldsymbol{\psi^u},\boldsymbol{\rho^u}), (\boldsymbol{w}, & \boldsymbol{\psi^w})\big) = L\big((\boldsymbol{w},\boldsymbol{\psi^w})\big), \end{split} \end{equation}\]

(25)\[\begin{split}\begin{equation} \begin{split} \int_{\Omega}\big(\psi_{11}-\partial_1 u_1\big)\rho^w_{11}\mathrm{d}\Omega &= 0, \\ \int_{\Omega}\big(\psi_{12}-\partial_1 u_2\big)\rho^w_{12}\mathrm{d}\Omega &= 0, \\ \int_{\Omega}\big(\psi_{21}-\partial_2 u_1\big)\rho^w_{21}\mathrm{d}\Omega &= 0, \\ \int_{\Omega}\big(\psi_{22}-\partial_2 u_2\big)\rho^w_{22}\mathrm{d}\Omega &= 0 \end{split} \end{equation}\end{split}\]

pro

(26)\[\forall\boldsymbol{w}\in\hat{V}_2,\,\forall\boldsymbol{\psi^w}\in\hat{V}_{2\times 2} \quad\mathrm{a}\quad \forall\boldsymbol{\rho^w}\in\hat{W}_{2\times 2},\]

kde

(27)\[\begin{split}\begin{equation} \begin{split} a & \big((\boldsymbol{u},\boldsymbol{\psi_u},\boldsymbol{\rho_u}), (\boldsymbol{w},\boldsymbol{\psi_w},\boldsymbol{\rho_w})\big) \\ &= \int_{\Omega}\big(\boldsymbol{\sigma}(\boldsymbol{u}): \boldsymbol{\varepsilon}(\boldsymbol{w}) +\boldsymbol{\tau}(\boldsymbol{\psi_u}):\cdotp \boldsymbol{\hat{\eta}}(\boldsymbol{\psi_w}) +\boldsymbol{\rho_u}:\boldsymbol{\psi_w} -\boldsymbol{\rho_u}:\nabla\boldsymbol{w}\big)\mathrm{d}\Omega, \end{split} \end{equation}\end{split}\]

(28)\[ L\big((\boldsymbol{w},\boldsymbol{\psi_w})\big)= \int_{\partial\Omega}\boldsymbol{f}_2\cdotp\boldsymbol{w}\mathrm{d}\partial\Omega.\]

Po zavedení nové míry hranice příkazem Measure (očíslování hranic bylo importováno z GMSH) se výše uvedená slabá formulace definuje v DOLFINu následovně,

ds=Measure("ds",domain=mesh,subdomain_data=boundaries)

F1=StressT(u)[i,j]*StrainT(w)[i,j]*dx-u_Lagrange[i,j]*w[j].dx(i)*dx-tr2[j]*w[j]*ds(2)
F2=HStress(u_RStrain)[j,i,k]*RStrainGrad(w_RStrain)[j,i,k]*dx+u_Lagrange[i,k]*w_RStrain[i,k]*dx
F30=u_RStrain[0,0]*w_Lagrange[0,0]*dx-u[0].dx(0)*w_Lagrange[0,0]*dx
F31=u_RStrain[0,1]*w_Lagrange[0,1]*dx-u[1].dx(0)*w_Lagrange[0,1]*dx
F32=u_RStrain[1,0]*w_Lagrange[1,0]*dx-u[0].dx(1)*w_Lagrange[1,0]*dx
F33=u_RStrain[1,1]*w_Lagrange[1,1]*dx-u[1].dx(1)*w_Lagrange[1,1]*dx
F=F1+F2+F30+F31+F32+F33

a=lhs(F)
L=rhs(F)

Zbývá slabou formulaci problému vyřešit a vyjádřit posuvy \(\boldsymbol{u}\) nebo jeho složky \(u_x\) a \(u_y\) a pomocí výše definované funkce StressT vyjádřit tenzor napětí \(\boldsymbol{\sigma}\).

mx=Function(MX)
(A,b)=assemble_system(a,L,bcs,finalize_tensor=True)
solve(A,mx.vector(),b,"lu")

u,u_RStrain,u_Lagrange=mx.split()
u_x,u_y=u.split()

W=TensorFunctionSpace(mesh,"CG",1)
sigma=project(StressT(u),W)

Jedna z možností, jak si prohlédnout výsledky je s pomocí velice sofistikovaného programu paraview.org. K tomu stačí výsledky uložit ve formátu *.pvd následovně.

file1=File('mindlin_crack_u.pvd')
file1 << u

file2=File('mindlin_crack_s.pvd')
file2 << sigma

Zbývá uvést některé výstupy z programu ParaView. Pro materiálové charakteristiky \(E=2.1\times 10^5\,\mathrm{MPa}\), \(\nu=0.25\) a \(l=0.01\,\mathrm{mm}\). Nejdříve napětí \(\sigma_{yy}\) (kliknutím se obrázek zvětší).

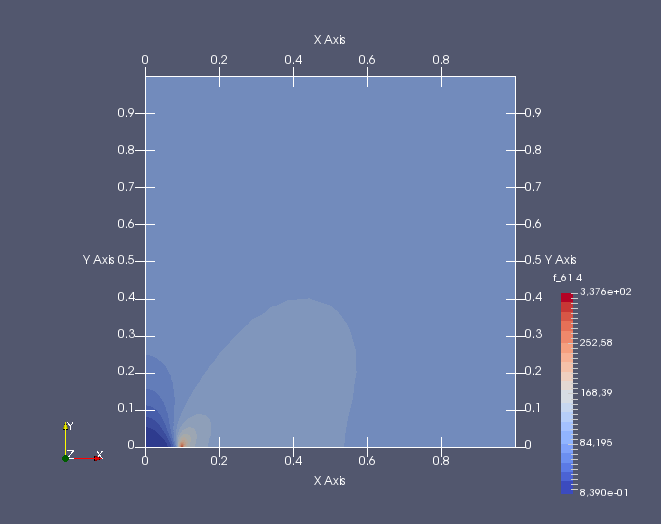
Dále pak detail kořene trhliny a jeho rozevření, které je zvětšeno \(100\times\) (kliknutím se obrázek zvětší).

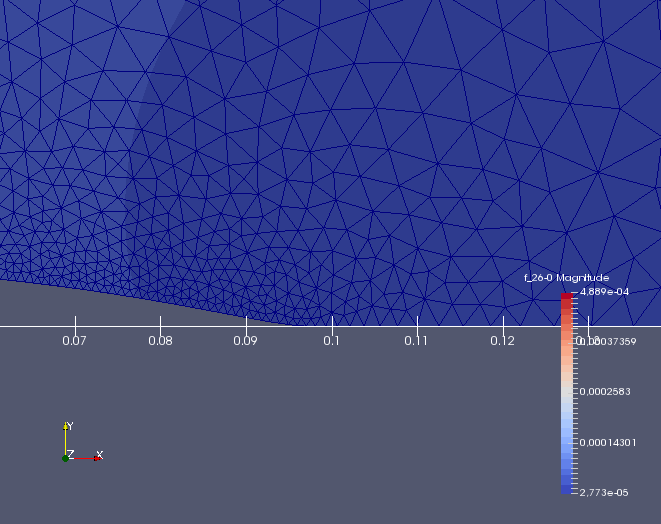
Dále pak pro charakteristiku \(l=0.01\times 10^{-5}\,\mathrm{mm}\). U napětí \(\sigma_{yy}\) je použit stejná škála hodnot, aby se daly oba případy změny parametru \(l\) lépe porovnat. Extrémní hodnoty napětí pro menší téměř nulovou hodnotu \(l\) jsou o dva řády vyšší než pro \(l=0.01\,\mathrm{mm}\) (kliknutím se obrázek zvětší).

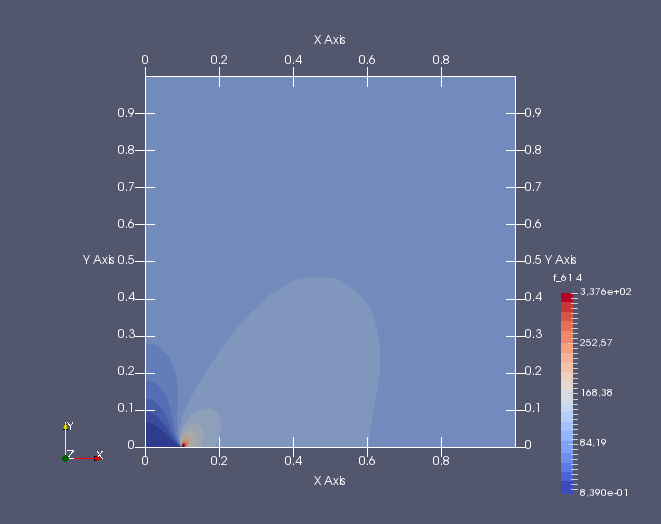
Detail kořene trhliny a jeho rozevření, které je opět zvětšeno \(100\times\) (kliknutím se obrázek zvětší)

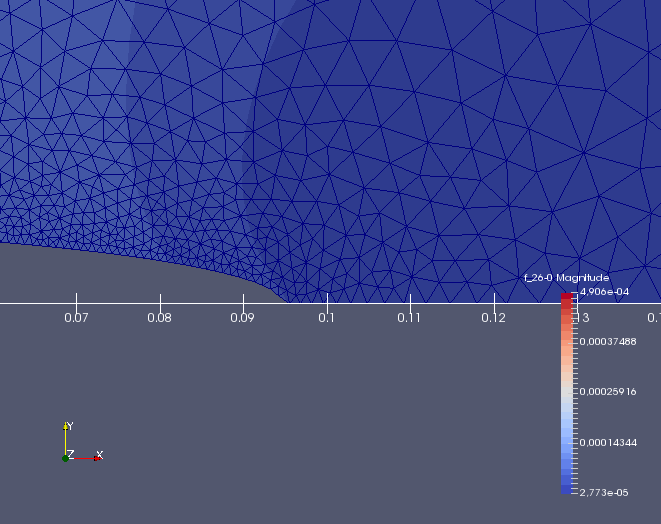
Výše popsané skripty lze stáhnout zde a zde.

Literatura

[1]

Toupin, R. A., Elastic materials with couple stresses, Arch. Rational Mech. Anal., 11, 385-414, 1962.

[2]

Mindlin, R. D., Micro-structure in linear elasticity, Arch. Rational Mech. Anal., 16, 51-78, 1964.

[3]

Shu, J. Y., King, W. E., Fleck, N. A., Finite elements for materials with strain gradient effects, Int. J. Numer. Meth. Engng., 44, 373-391, 1999.

[4] (1,2)

Phunpeng, V., Baiz, P. M., Mixed finite element formulations for strain-gradient elasticity problems using the FEniCS environment, Finite Elements in Analysis and Design, 96, 23-40, 2015.