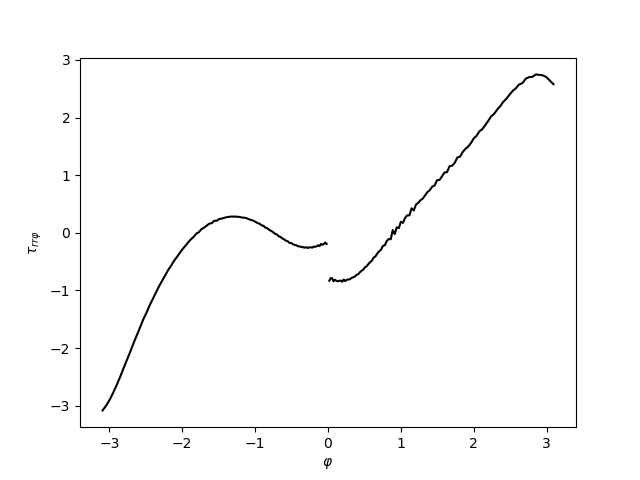
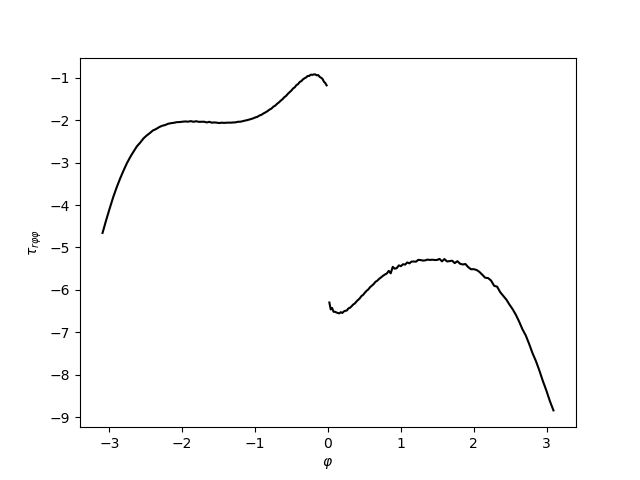
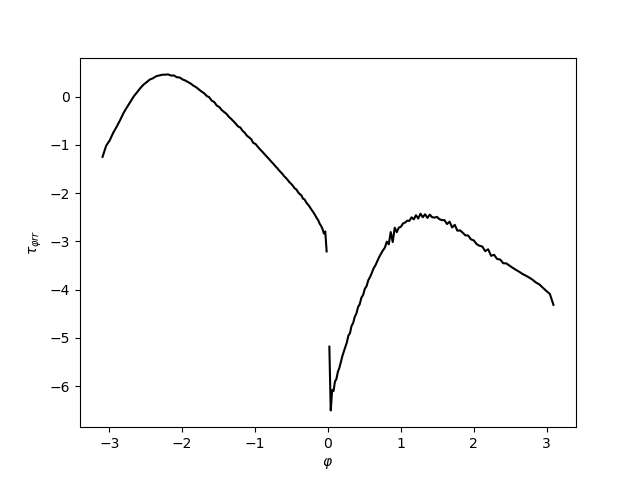
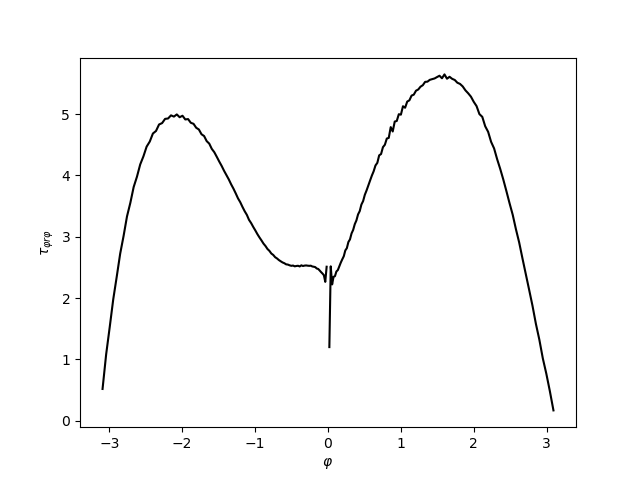
Základní vztahy
Rovnice rovnováhy se v gradientní pružnosti mohou napsat pomocí vektorového zápisu následovně
(1)\[\nabla\cdot(\boldsymbol{T}-\nabla\boldsymbol{\hat{T}}) = 0,\]
kde \(\boldsymbol{T}\) je Cauchyho tenzor napětí a \(\boldsymbol{\hat{T}}\) je dipolární tenzor napětí, pro který platí
(2)\[\boldsymbol{\hat{T}} = l^2\nabla\otimes\boldsymbol{T}.\]
Zde \(l\) značí vnitřní délkový parametr materiálu a tenzorový součin \(\nabla\otimes\boldsymbol{T}\) se může v kartézském souřadnicovém systému daném jednotkovými vektory \((\boldsymbol{e}_x,\boldsymbol{e}_y)\) psát následovně
(3)\[\begin{split}\nabla\otimes\boldsymbol{T} &=
\partial_xT_{xx}\boldsymbol{e}_x\otimes\boldsymbol{e}_x\otimes\boldsymbol{e}_x
+\partial_xT_{xy}(\boldsymbol{e}_x\otimes\boldsymbol{e}_x\otimes\boldsymbol{e}_y
+\boldsymbol{e}_x\otimes\boldsymbol{e}_y\otimes\boldsymbol{e}_x) \\
&+ \partial_xT_{yy}\boldsymbol{e}_x\otimes\boldsymbol{e}_y\otimes\boldsymbol{e}_y
+\partial_yT_{xx}\boldsymbol{e}_y\otimes\boldsymbol{e}_x\otimes\boldsymbol{e}_x \\
&+ \partial_yT_{xy}(\boldsymbol{e}_y\otimes\boldsymbol{e}_x\otimes\boldsymbol{e}_y
+\boldsymbol{e}_y\otimes\boldsymbol{e}_y\otimes\boldsymbol{e}_x)
+\partial_yT_{yy}\boldsymbol{e}_y\otimes\boldsymbol{e}_y\otimes\boldsymbol{e}_y\end{split}\]
a v polárním souřadnicovém systému daného dvojicí jednotkových vektorů \((\boldsymbol{e}_r,\boldsymbol{e}_\theta)\) o něco komplikovaněji
(4)\[\begin{split}\nabla\otimes\boldsymbol{T} &=
\partial_rT_{rr}\boldsymbol{e}_r\otimes\boldsymbol{e}_r\otimes\boldsymbol{e}_r
+\partial_rT_{r\theta}\boldsymbol{e}_r\otimes\boldsymbol{e}_r\otimes\boldsymbol{e}_\theta \\
&+ \partial_rT_{r\theta}\boldsymbol{e}_r\otimes\boldsymbol{e}_\theta\otimes\boldsymbol{e}_r
+\partial_rT_{\theta\theta}\boldsymbol{e}_r\otimes\boldsymbol{e}_\theta\otimes\boldsymbol{e}_\theta \\
&+ \frac{1}{r}(\partial_\theta T_{rr}-2T_{r\theta})
\boldsymbol{e}_\theta\otimes\boldsymbol{e}_r\otimes\boldsymbol{e}_r \\
&+\frac{1}{r}(T_{rr}-T_{\theta\theta}+\partial_\theta T_{r\theta})
\boldsymbol{e}_\theta\otimes\boldsymbol{e}_r\otimes\boldsymbol{e}_\theta \\
&+ \frac{1}{r}(T_{rr}-T_{\theta\theta}+\partial_\theta T_{r\theta})
\boldsymbol{e}_\theta\otimes\boldsymbol{e}_\theta\otimes\boldsymbol{e}_r \\
&+ \frac{1}{r}(2T_{r\theta}+\partial_\theta T_{\theta\theta})
\boldsymbol{e}_\theta\otimes\boldsymbol{e}_\theta\otimes\boldsymbol{e}_\theta.\end{split}\]
Okrajové podmínky mají tvar
(5)\[\begin{split}\boldsymbol{\nu} =& \boldsymbol{n}\cdot(\nabla\otimes\boldsymbol{u})
=(\boldsymbol{u}\otimes\nabla)\cdot\boldsymbol{n}, \\
\boldsymbol{t} =& \boldsymbol{n}\cdot(\boldsymbol{T}-\nabla\cdot\hat{\boldsymbol{T}})
-\overset{s}{\nabla}\cdot(\boldsymbol{n}\cdot\hat{\boldsymbol{T}})
+(\overset{s}{\nabla}\cdot\boldsymbol{n})
\boldsymbol{n}\otimes\boldsymbol{n}
:\hat{\boldsymbol{T}} \\
=& \boldsymbol{n}\cdot(\boldsymbol{T}-\nabla\cdot\hat{\boldsymbol{T}})
-\overset{s}{\nabla}\cdot(\boldsymbol{n}\cdot\hat{\boldsymbol{T}})
+(\overset{s}{\nabla}\cdot\boldsymbol{n})\boldsymbol{n}
\cdot(\boldsymbol{n}\cdot\hat{\boldsymbol{T}}), \\
\boldsymbol{r} =& \boldsymbol{nn}:\hat{\boldsymbol{T}}
=\boldsymbol{n}\cdot(\boldsymbol{n}\cdot\hat{\boldsymbol{T}}),\end{split}\]
kde
(6)\[\overset{s}{\nabla}=(\boldsymbol{I}-\boldsymbol{n}\otimes\boldsymbol{n})\cdot\nabla.\]
Následující vztahy jsou odvozeny v sget3.lyx. V případě kartézského souřadnicového systému s normálou \(\boldsymbol{n}\equiv\pm\boldsymbol{e}_x\) platí
(7)\[\begin{split}\overset{s}{\nabla} &= (\boldsymbol{I}-\boldsymbol{n}\otimes\boldsymbol{n})\cdot\nabla \\
&= (\boldsymbol{e}_x\otimes\boldsymbol{e}_x
+\boldsymbol{e}_y\otimes\boldsymbol{e}_y
-\boldsymbol{e}_x\otimes\boldsymbol{e}_x)
\cdot(\boldsymbol{e}_x\partial_x+\boldsymbol{e}_y\partial_y) \\
&= (\boldsymbol{e}_y\otimes\boldsymbol{e}_y)
\cdot(\boldsymbol{e}_x\partial_x+\boldsymbol{e}_y\partial_y) \\
&= \boldsymbol{e}_y\partial_y\end{split}\]
a okrajové podmínky (5) mají tvar
(8)\[\begin{split}\boldsymbol{\nu} &= \pm(\partial_xu_x\boldsymbol{e}_x+\partial_xu_y\boldsymbol{e}_y), \\
\boldsymbol{t} &= \pm\boldsymbol{e}_x(T_{xx}-\partial_x\hat{T}_{xxx}-\partial_y\hat{T}_{yxx}
-\partial_y\hat{T}_{xxy}\mp\hat{T}_{xxx}) \\
&\pm \boldsymbol{e}_y(T_{xy}-\partial_x\hat{T}_{xxy}-\partial_y\hat{T}_{yxy}
-\partial_y\hat{T}_{xyy}\mp\hat{T}_{xxy}) \\
\boldsymbol{r} &= \boldsymbol{e}_x\hat{T}_{xxx}+\boldsymbol{e}_y\hat{T}_{xxy}.\end{split}\]
V případě normály \(\boldsymbol{n}\equiv\pm\boldsymbol{e}_y\) platí
(9)\[\begin{split}\overset{s}{\nabla} &= (\boldsymbol{I}-\boldsymbol{n}\otimes\boldsymbol{n})\cdot\nabla \\
&= (\boldsymbol{e}_x\otimes\boldsymbol{e}_x
+\boldsymbol{e}_y\otimes\boldsymbol{e}_y
-\boldsymbol{e}_y\otimes\boldsymbol{e}_y)
\cdot(\boldsymbol{e}_x\partial_x+\boldsymbol{e}_y\partial_y) \\
&= (\boldsymbol{e}_x\otimes\boldsymbol{e}_x)
\cdot(\boldsymbol{e}_x\partial_x+\boldsymbol{e}_y\partial_y) \\
&= \boldsymbol{e}_x\partial_x\end{split}\]
a
(10)\[\begin{split}\boldsymbol{\nu} &= \pm(\partial_yu_x\boldsymbol{e}_x+\partial_yu_y\boldsymbol{e}_y), \\
\boldsymbol{t} &= \pm\boldsymbol{e}_x(T_{yx}-\partial_x\hat{T}_{xxy}-\partial_y\hat{T}_{yxy}
-\partial_x\hat{T}_{yxx}\mp\hat{T}_{yxy}) \\
&\pm \boldsymbol{e}_y(T_{yy}-\partial_x\hat{T}_{xyy}-\partial_y\hat{T}_{yyy}
-\partial_x\hat{T}_{yxy}\mp\hat{T}_{yyy}), \\
\boldsymbol{r} &= \boldsymbol{e}_x\hat{T}_{yyx}+\boldsymbol{e}_y\hat{T}_{yyy}.\end{split}\]
V polárním souřadnicovém systému v případě normály \(\boldsymbol{n}\equiv\boldsymbol{e}_rn_r(\theta)+\boldsymbol{e}_\theta n_\theta(\theta)\) platí
(11)\[\begin{split}\overset{s}{\nabla} &= (\boldsymbol{I}-\boldsymbol{n}\otimes\boldsymbol{n})\cdot\nabla \\
&= [\boldsymbol{e}_r\otimes\boldsymbol{e}_r
+\boldsymbol{e}_\theta\otimes\boldsymbol{e}_\theta \\
&- (\boldsymbol{e}_r\otimes\boldsymbol{e}_rn_r^2
-\boldsymbol{e}_r\otimes\boldsymbol{e}_\theta n_rn_\theta
-\boldsymbol{e}_\theta\otimes\boldsymbol{e}_rn_rn_\theta
+\boldsymbol{e}_\theta\otimes\boldsymbol{e}_\theta n_\theta^2)]
\cdot(\boldsymbol{e}_r\partial_r+\boldsymbol{e}_\theta\frac{1}{r}\partial_\theta) \\
&= [\boldsymbol{e}_r\otimes\boldsymbol{e}_rn_\theta^2
-\boldsymbol{e}_r\otimes\boldsymbol{e}_\theta n_rn_\theta
-\boldsymbol{e}_\theta\otimes\boldsymbol{e}_rn_rn_\theta
+\boldsymbol{e}_\theta\otimes\boldsymbol{e}_\theta n_r^2]
\cdot(\boldsymbol{e}_r\partial_r+\boldsymbol{e}_\theta\frac{1}{r}\partial_\theta) \\
&= \boldsymbol{e}_r(n_\theta^2\partial_r-n_rn_\theta\frac{1}{r}\partial_\theta)
+\boldsymbol{e}_\theta(-n_rn_\theta\partial_r+\frac{1}{r}n_r^2\partial_\theta)\end{split}\]
a také
(12)\[\begin{split}\boldsymbol{\nu} &= \boldsymbol{e}_r[n_r\partial_ru_r+n_\theta\frac{1}{r}
(\partial_\theta u_r-u_\theta)] \\
&+ \boldsymbol{e}_\theta[n_r\partial_{r}u_\theta+n_\theta\frac{1}{r}(\partial_\theta u_\theta+u_r)] \\
\boldsymbol{t} &= \boldsymbol{e}_r[n_r\boldsymbol{T}_{rr}+n_\theta\boldsymbol{T}_{r\theta} \\
&- n_r(\partial_r\hat{T}_{rrr}+\frac{1}{r}\partial_\theta\hat{T}_{\theta rr}
+\frac{1}{r}\hat{T}_{rrr}-\frac{2}{r}\hat{T}_{\theta r\theta}) \\
&- n_\theta(\partial_r\hat{T}_{rr\theta}
+\frac{1}{r}\partial_\theta\hat{T}_{\theta r\theta}
+\frac{1}{r}\hat{T}_{rr\theta}+\frac{1}{r}\hat{T}_{\theta rr}
-\frac{1}{r}\hat{T}_{\theta\theta\theta}) \\
&- n_\theta^2\partial_r(n_r\hat{T}_{rrr}+n_\theta\hat{T}_{\theta rr})
+n_rn_\theta\frac{1}{r}\partial_\theta
(n_r\hat{T}_{rrr}+n_\theta\hat{T}_{\theta rr}) \\
&- 2n_rn_\theta\frac{1}{r}(n_r\hat{T}_{rr\theta}+n_\theta\hat{T}_{\theta r\theta}) \\
&- \frac{1}{r}n_r^2[n_r(\hat{T}_{rrr}-\hat{T}_{r\theta\theta})
+n_\theta(\hat{T}_{\theta rr}-\hat{T}_{\theta\theta\theta})] \\
&- \frac{1}{r}n_r^2\partial_\theta(n_r\hat{T}_{rr\theta}+n_\theta\hat{T}_{\theta r\theta})
+n_rn_\theta\partial_r(n_r\hat{T}_{r r\theta}+n_\theta\hat{T}_{\theta r\theta}) \\
&+ n_r^2\hat{T}_{rrr}
+n_rn_\theta(\hat{T}_{\theta rr}+\hat{T}_{rr\theta})
+n_\theta^2\hat{T}_{\theta r\theta}] \\
&+ \boldsymbol{e}_\theta[n_r\boldsymbol{T}_{r\theta}
+n_\theta\boldsymbol{T}_{\theta\theta} \\
&- n_r(\partial_r\hat{T}_{rr\theta}+\frac{1}{r}\partial_\theta\hat{T}_{\theta r\theta}
+\frac{1}{r}\hat{T}_{rr\theta}+\frac{1}{r}\hat{T}_{\theta rr}
-\frac{1}{r}\hat{T}_{\theta\theta\theta}) \\
&- n_\theta(\partial_r\hat{T}_{r\theta\theta}+\frac{1}{r}\partial_\theta\hat{T}_{\theta\theta\theta}
+\frac{1}{r}\hat{T}_{r\theta\theta}+\frac{2}{r}\hat{T}_{\theta r\theta}) \\
&+ n_rn_\theta\frac{1}{r}[n_r(\hat{T}_{rrr}-\hat{T}_{r\theta\theta})
+n_\theta(\hat{T}_{\theta rr}-\hat{T}_{\theta\theta\theta})] \\
&+ n_rn_\theta\frac{1}{r}\partial_\theta(n_r\hat{T}_{rr\theta}+n_\theta\hat{T}_{\theta r\theta})
-n_\theta^2\partial_r(n_r\hat{T}_{rr\theta}+n_\theta\hat{T}_{\theta r\theta}) \\
&- \frac{2}{r}n_r^2(n_r\hat{T}_{rr\theta}+n_\theta\hat{T}_{\theta r\theta}) \\
&+ n_rn_\theta\partial_r(n_r\hat{T}_{r\theta\theta}+n_\theta\hat{T}_{\theta\theta\theta})
-\frac{1}{r}n_r^2\partial_\theta(n_r\hat{T}_{r\theta\theta}
+n_\theta\hat{T}_{\theta\theta\theta})] \\
&+ \boldsymbol{e}_\theta[n_r^2\hat{T}_{rr\theta}+n_rn_\theta
(\hat{T}_{\theta r\theta}+\hat{T}_{r\theta\theta})
+n_\theta^2\hat{T}_{\theta\theta\theta}]\end{split}\]
Předpokládá se izotropní materiál, takže konstitutivní vztah pro tenzor napětí \(\boldsymbol{T}\) se má tvar
(13)\[\begin{split}\boldsymbol{T} &= \lambda\mathrm{Tr}(\boldsymbol{S})\boldsymbol{I}
+2\mu\boldsymbol{S} \\\end{split}\]
kde \(\lambda\) a \(\mu\) jsou Lamého konstanty. Jestliže \(\nu\) je Poissonova konstanta, pak
(14)\[\begin{split}\lambda &= \frac{E\nu}{(1+\nu)(1-2\nu)}, \\
\mu &= \frac{E}{2(1+\nu)}.\end{split}\]
Dále, \(\boldsymbol{S}\) je tenzor deformace, pro který v polárních souřadnicích platí, že
(15)\[\begin{split}\boldsymbol{S}=\frac{1}{2}(\nabla\otimes\boldsymbol{u}+\boldsymbol{u}\otimes\nabla)
=\left[
\begin{array}{ll}
\partial_ru_r & \frac{1}{2}\partial_ru_\theta+\frac{1}{2r}(-u_\theta+\partial_\theta u_r) \\
\frac{1}{2}\partial_ru_\theta+\frac{1}{2r}(-u_\theta+\partial_\theta u_r) &
\frac{1}{r}(u_r+\partial_\theta u_\theta)
\end{array}
\right]\end{split}\]
a \(\mathrm{Tr}\) je trasa tenzoru a \(\boldsymbol{I}\) je jednotkový tenzor druhého řádu, tj.
(16)\[\begin{split}\mathrm{Tr}(\boldsymbol{S}) &= S_{rr}+S_{\theta\theta}, \quad
\boldsymbol{I} = \left[
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}
\right].\end{split}\]
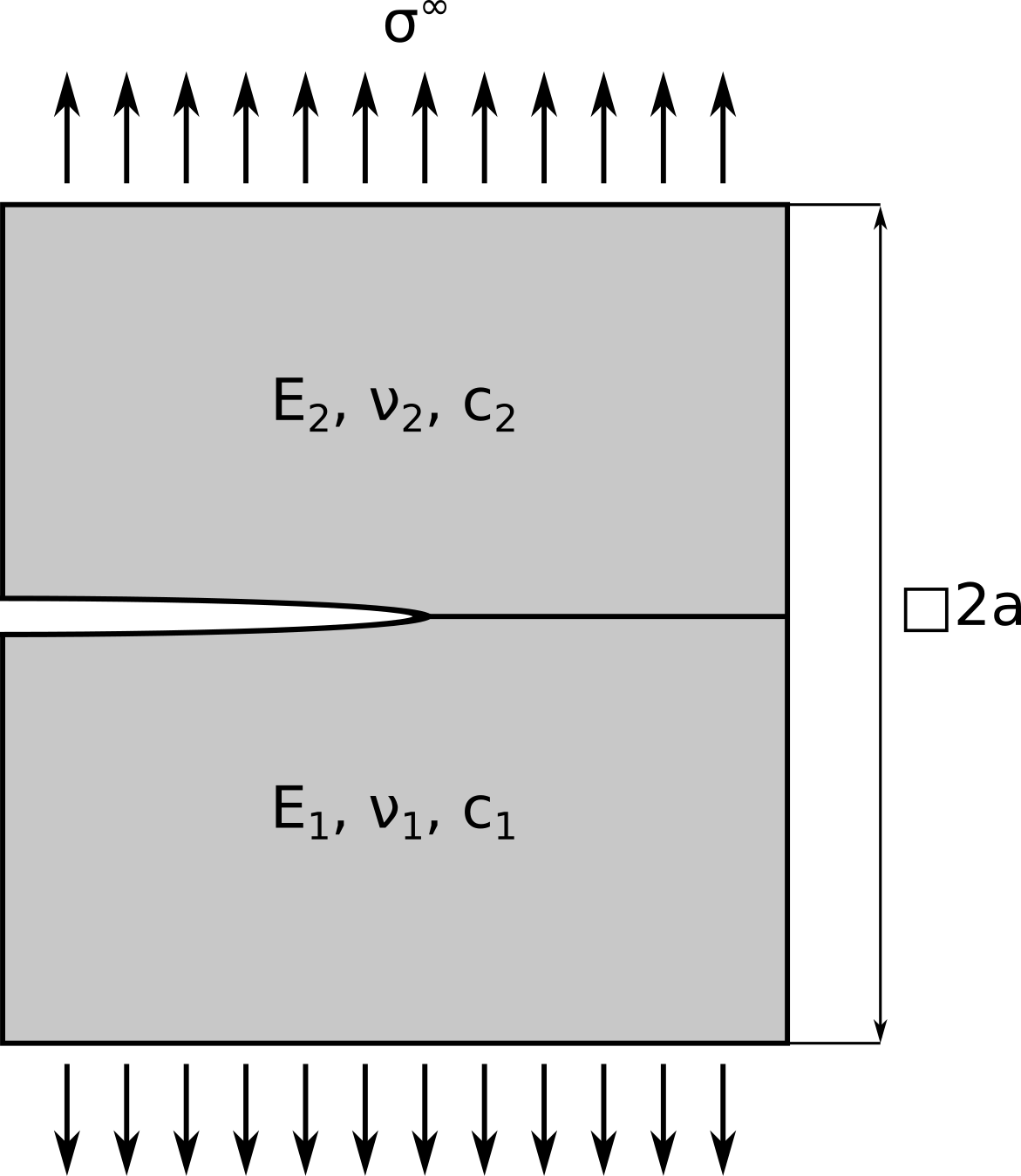
V úloze o trhlině na rozhraní se vychází z algoritmu popsaného v Gradientní pružnost - trhlina v homogenním materiálu. Rovnice rovnováhy (1) se po dosazení (13) a (15) za předpokladu dominance gradientů deformace může rozepsat do dvou diferenciálních rovnic ve tvaru
(17)\[\begin{split}\nabla^2s_r-\frac{1}{r^2}s_r-2\frac{1}{r^2}\partial_\theta s_\theta &=0, \\
\nabla^2s_\theta-\frac{1}{r^2}s_\theta+2\frac{1}{r^2}\partial_\theta s_r &=0,\end{split}\]
kde
(18)\[\begin{split}s_r &= 2(1-\nu)\partial_r(\partial_ru_r+\frac{1}{r}u_r+\frac{1}{r}\partial_\theta u_\theta) \\
&- (1-2\nu)\frac{1}{r}\partial_\theta(\partial_ru_\theta-\frac{1}{r}\partial_\theta u_r
+\frac{1}{r}u_\theta), \\
s_\theta &= (1-2\nu)\partial_r(\partial_ru_\theta+\frac{1}{r}u_\theta
-\frac{1}{r}\partial_\theta u_r) \\
&+ 2(1-\nu)\frac{1}{r}\partial_\theta(\partial_ru_r+\frac{1}{r}u_r
+\frac{1}{r}\partial_\theta u_\theta).\end{split}\]
Standardní separací proměnných \(r\) a \(\theta\) se řešení (17) předpokládá ve tvaru
(19)\[\begin{split}u_r=r^pU_r(\theta) &= r^p\sum_i \{A_i\cos(p-i)\theta+B_i\sin(p-i)\theta\}, \\
u_\theta=r^pU_\theta(\theta) &= r^p\sum_i \{C_i\cos(p-i)\theta+D_i\sin(p-i)\theta\}.\end{split}\]
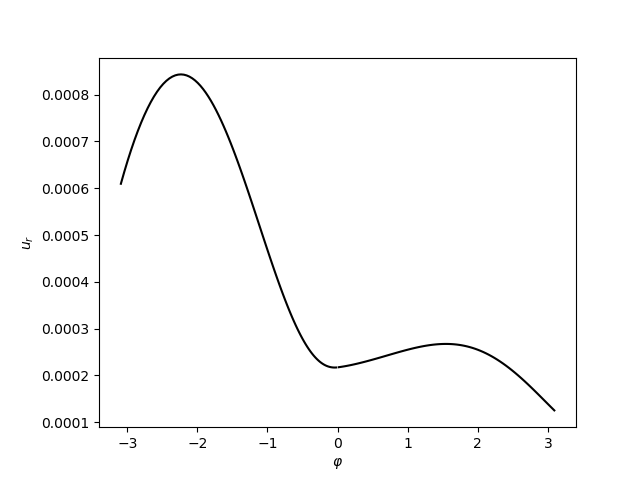
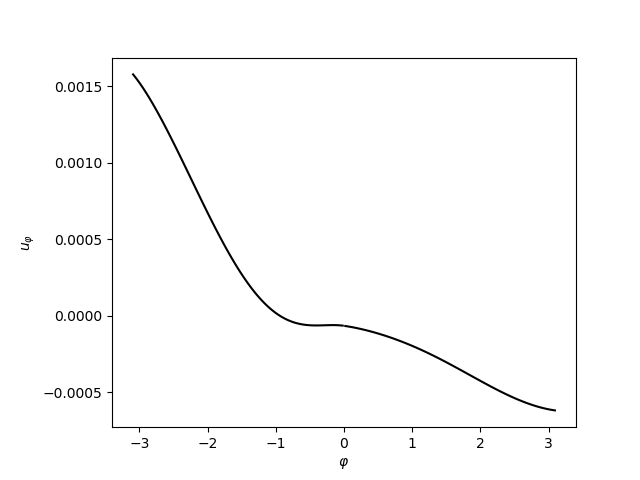
Jestliže se označí horní a dolní materiál indexy \(J=I,II\), pak se přímým dosazením (19) do (17) dostane řešení ve tvaru
(20)\[\begin{split}u_r^J &= r\{\Gamma_1^J+\Gamma_2^J\cos2\theta+\Gamma_3^J\sin2\theta\} \\
&+ r^p\{A_1^J\cos(p-1)\theta+B_1^J\sin(p-1)\theta
+A_2^J\cos(p+1)\theta+B_2^J\sin(p+1)\theta \\
&+ A_3^J\cos(p-3)\theta+B_3^J\sin(p-3)\theta\}, \\
u_\theta^J &= r\{\Gamma_4^J+\Gamma_3^J\cos2\theta-\Gamma_2^J\sin2\theta\} \\
&+ r^p\{B_4^J\cos(p-1)\theta+A_4^J\sin(p-1)\theta
+B_2^J\cos(p+1)\theta-A_2^J\sin(p+1)\theta \\
&+ \frac{(p+1)(\lambda^J+\mu^J)+4\mu^J}{(p-3)(\lambda^J+\mu^J)-4\mu^J}
[B_3^J\cos(p-3)\theta-A_3^J\sin(p-3)\theta]\},\end{split}\]