Piezoelektricita - zóna přepólování u bimateriálového vrubu

Součinitele intenzity napětí (FEniCS 2019.1.0)

Veškerou teorii včetně popisu LES formalismu a stanovení součinitelů intenzity napětí s pomocí \(\Psi\)-integrálu u piezoelektrických bimateriálových vrubů lze nalézt v [1] a [2]. Skripty pro FEniCS ve verzi (2019.1.0) lze stáhnout níže a potřebné vztahy, které jsou v nich použité jsou zde.

Změna polarizace ve vrcholu vrubu

Kritérium změny polarizace před čelem vrubu, viz [3] a [4]

(1)\[\sigma_{ij}\Delta\varepsilon_{ij}+E_i\Delta P_i\geq2E_CP_0,\]

kde \(E_C\) je koercitivní elektrické pole, \(P_0\) je remanentní polarizace, \(\sigma_{ij}\) a \(E_i\) jsou složky tenzoru a vektoru aktuálního napětí a elektrického pole a pro \(\Delta\varepsilon_{ij}\) a \(\Delta P_i\) platí

(2)\[\begin{split}\Delta\varepsilon_{ij}=-\varepsilon_D\left[ \begin{array}{ll} \cos(2\phi) & \sin(2\phi) \\ \sin(2\phi) & -\cos(2\phi) \end{array} \right]\end{split}\]

a

(3)\[\begin{split}\Delta P_i=bP_0\left[ \begin{array}{l} \sin(\phi+\varphi) \\ -\cos(\phi+\varphi) \end{array} \right].\end{split}\]

Zde \(\phi\) je úhel mezi osou \(x\) a směrem vláken (osou \(c\) čtverečné krystalové mřížky) a pro úhel \(\varphi\) platí

(4)\[\begin{split}\varphi=\left\{ \begin{array}{ll} +\pi/4 & \mathrm{pro\quad}+90^\circ, \\ -\pi/4 & \mathrm{pro\quad}-90^\circ, \\ \pm\pi/2 & \mathrm{pro\quad}\pm180^\circ. \end{array} \right.\end{split}\]

Podobně pro \(b\) platí

(5)\[\begin{split}b=\left\{ \begin{array}{ll} -\sqrt{2} & \mathrm{pro\quad}+90^\circ, \\ \sqrt{2} & \mathrm{pro\quad}-90^\circ, \\ -2 & \mathrm{pro\quad}\pm180^\circ. \end{array} \right.\end{split}\]

Zbývá parametr deformace čtverečné mřížky \(\varepsilon_D=(c-a)/a_0\) závisející na jejich krystalografických parametrech \(a\) a \(c\).

Vliv změny polarizace na součinitele intenzity napětí

U vlivu změny polarizace na hodnoty zobecněných součinitelů intenzity napětí se předpokládá pouze účinek mechanických (elastických) změn v oblasti přepólování [3]. Zatížení bimateriálového vrubu vlivem deformace \(\varepsilon_D\) v oblasti přepólování je ekvivalentní zatížení vrubu efektivní objemovou silou \(\Delta\boldsymbol{f}\), viz [5], která se dostane z rovnic rovnováhy

(6)\[\Delta\sigma_{ij,j}+\Delta f_j=0\quad\Rightarrow\quad \Delta f_j=-\Delta\sigma_{ij,i}.\]

Vztah pro vyjádření zobecněných součinitelů intenzity napětí \(K^{(\alpha)}\) pomocí \(\Psi\)-integrálu se může zobecnit do tvaru, [6],

(7)\[\begin{split}\begin{equation} \begin{split} K^{(\alpha)} =& \int_{S_T+S_N}h_k^{(\alpha)}\big(x_1,x_2\big)F_k\mathrm{d}s - \int_{S_U}H_k^{(\alpha)}\big(x_1,x_2\big)U_k\mathrm{d}s \\ & + \int_Ah_k^{(\alpha)}\big(x_1,x_2\big)f_k\mathrm{d}A, \end{split} \end{equation}\end{split}\]

kde \(F_k\) a \(U_k\) jsou vektor napětí a posuvy na hranicích \(S_T\cup S_N\), a \(S_U\) oblasti \(A\). Část hranice \(S_N\) značí líce vrubu. Pro váhové funkce \(h_k^{(\alpha)}\) a \(H_k^{(\alpha)}\) jsou pomocná řešení z [1] nebo [2], která jsou navíc normovaná

(8)\[\begin{split}\begin{equation} \begin{split} \boldsymbol{h^{(\alpha)}} =& \frac{\boldsymbol{\hat{u}}_\alpha}{Y}, \\ \boldsymbol{H_k^{(\alpha)}} =& \frac{\boldsymbol{\hat{t}}_\alpha}{Y}. \end{split} \end{equation}\end{split}\]

Normovací člen \(Y\) má tvar [1], [2]

(9)\[Y=\int_{\omega_1}^{\omega_2}\big(\boldsymbol{u}^T\cdot\boldsymbol{\hat{t}} - \boldsymbol{\hat{u}}^T\cdot\boldsymbol{t}\big)r\mathrm{d}\theta,\]

kde \(\omega_1\) a \(\omega_2\) jsou úhly rozevření vrubu, \(r\) je vzdálenost od jeho vrcholu, \(\boldsymbol{u}\) a \(\boldsymbol{t}\) jsou tzv. regulární řešení. Změna vlivem přepólování se děje v posledním plošném integrálu vztahu (7), pro který po dosazení druhého vztahu z (6) platí

(10)\[\Delta K^{(\alpha)} = -\int_Ah_k^{(\alpha)}\big(x_1,x_2\big)\Delta\sigma_{ik,i}\mathrm{d}A.\]

Napětí \(\Delta\sigma_{ij}\) se dostane z konstitutivních vztahů, viz [1], [2]

(11)\[\begin{split}\begin{equation} \begin{split} \boldsymbol{\varepsilon} =& \hat{\boldsymbol{S}}_D^\prime\boldsymbol{\sigma} + \hat{\boldsymbol{g}}^{\prime T}\boldsymbol{D}, \\ -\boldsymbol{E} =& \hat{\boldsymbol{g}}^\prime\boldsymbol{\sigma} - \hat{\boldsymbol{\beta}}_\sigma^\prime\boldsymbol{D}. \end{split} \end{equation}\end{split}\]

Za \(\boldsymbol{\varepsilon}\) se dosadí \(\Delta\boldsymbol{\varepsilon}\) dané vztahem (2), které je konstantní v oblasti změny polarizace. Protože se v dalším bude předpokládat, že jsou líce vrubu izolované, tj. \(\boldsymbol{D}=0\), platí

(12)\[\begin{split}\begin{equation} \begin{split} \Delta\boldsymbol{\sigma} =& \big(\hat{\boldsymbol{S}}_D^\prime\big)^{-1}\Delta\boldsymbol{\varepsilon}, \\ -\Delta\boldsymbol{E} =& \hat{\boldsymbol{g}}^\prime\Delta\boldsymbol{\sigma}. \end{split} \end{equation}\end{split}\]

V dalším se zanedbá vliv elektrické části zatížení způsobené změnou polarizace na zobecněné součinitele intenzity napětí. Napětí \(\Delta\boldsymbol{\sigma}\) je v oblasti \(A\) nulové a skokově se mění podél křivky \(L\) na nenulovou konstantní hodnotu v jisté malé oblasti přepólování v blízkosti vrcholu vrubu. Když pro ilustraci vybereme bod \([x_1^L,x_2^L]\) na křivce \(L\) tak, že vektor \(\mathrm{d}\boldsymbol{s}\) reprezentující orientaci křivky, má průměty \(\mathrm{d}x_1\) a \(\mathrm{d}x_2\) v kladném směru os \(x_1\) a \(x_2\), pak řezy složek tenzoru napětí \(\Delta\sigma_{ij}\) podél os \(x_1\) a \(x_2\) jsou "klesající" a "rostoucí" Heavisideovy funkce, jak ukazuje následující obrázek.

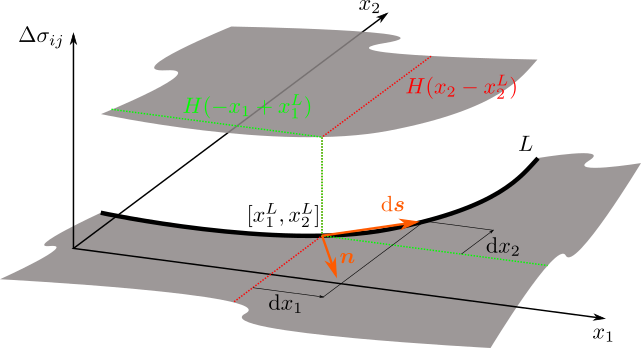
Skoková změna napětí \(\Delta\sigma_{ij}\) jako Heavysideové funkce v bodě \([x_1^L,x_2^L]\) křivky ohraničující zónu přepolóvání ve vrcholu vrubu.

To mimo jiné znamená

(13)\[\begin{split}\begin{equation} \begin{split} \frac{\mathrm{d}}{\mathrm{d}x_1}H(-x_1+x_1^L) =& -\delta(x_1-x_1^L), \\ \frac{\mathrm{d}}{\mathrm{d}x_2}H(x_2-x_2^L) =& \delta(x_2-x_2^L), \\ \end{split} \end{equation}\end{split}\]

a

(14)\[\mathrm{d}x_1=-n_y\mathrm{d}s,\quad\mathrm{d}x_2=n_x\mathrm{d}s,\]

kde \(\mathrm{d}s\) je velikost vektoru \(\mathrm{d}\boldsymbol{s}\). Jestliže \(x_1^{a,b}\) a \(x_2^{a,b}\) jsou krajní hodnoty křivky \(L\) na ose \(x_1\) a \(x_2\), pak pro integrál (10) platí

(15)\[\begin{split}\begin{equation} \begin{split} \Delta K^{(\alpha)} =& -\int\int_A\big[\Delta\sigma_{11,1}h_1^{(\alpha)}\big(x_1,x_2\big) + \Delta\sigma_{12,1}h_2^{(\alpha)}\big(x_1,x_2\big)\big] \mathrm{d}x_1\mathrm{d}x_2 \\ & - \int\int_A\big[\Delta\sigma_{21,2}h_1^{(\alpha)}\big(x_1,x_2\big) + \Delta\sigma_{22,2}h_2^{(\alpha)}\big(x_1,x_2\big)\big] \mathrm{d}x_2\mathrm{d}x_1 \\ =& \int\int_A\big[\Delta\sigma_{11} \delta\big(x_1-x_1^L(x_2)\big)h_1^{(\alpha)}\big(x_1,x_2\big) \\ & \qquad + \Delta\sigma_{12} \delta\big(x_1-x_1^L(x_2)\big)h_2^{(\alpha)}\big(x_1,x_2\big)\big] \mathrm{d}x_1\mathrm{d}x_2 \\ & -\int\int_A\big[\Delta\sigma_{21} \delta\big(x_2-x_2^L(x_1)\big)h_1^{(\alpha)}\big(x_1,x_2\big) \\ & \qquad + \Delta\sigma_{22} \delta\big(x_2-x_2^L(x_1)\big)h_2^{(\alpha)}\big(x_1,x_2\big)\big] \mathrm{d}x_2\mathrm{d}x_1 \\ =& \int_{x_2^a}^{x_2^b}\Delta\sigma_{11} h_1^{(\alpha)}\big(x_1^L(x_2),x_2\big)\mathrm{d}x_2 \\ &+ \int_{x_2^a}^{x_2^b}\Delta\sigma_{12} h_2^{(\alpha)}\big(x_1^L(x_2),x_2\big)\mathrm{d}x_2 \\ &- \int_{x_1^a}^{x_1^b}\Delta\sigma_{21} h_1^{(\alpha)}\big(x_1,x_2^L(x_1)\big)\mathrm{d}x_1 \\ &- \int_{x_1^a}^{x_1^b}\Delta\sigma_{22} h_2^{(\alpha)}\big(x_1,x_2^L(x_1)\big)\mathrm{d}x_1 \\ =& \int_L\big[\Delta\sigma_{11}h_1^{(\alpha)}\big(x_1,x_2\big)n_1 + \Delta\sigma_{12}h_2^{(\alpha)}\big(x_1,x_2\big)n_1 \\ & \quad + \Delta\sigma_{21}h_1^{(\alpha)}\big(x_1,x_2\big)n_2 + \Delta\sigma_{22}h_2^{(\alpha)}\big(x_1,x_2\big)n_2\big]\mathrm{d}s \\ =& \int_L\Delta\sigma_{ij}h_j^{(\alpha)}\big(x_1,x_2\big)n_i\mathrm{d}s. \end{split} \end{equation}\end{split}\]

Numerický příklad

Předpokládá se bimateriálový vrub složený z materiálů PZT-5H (horní materiál \(1\)) a BaTiO3 (dolní materiál \(2\)). Oba materiály mají natočená vlákna kolmo k rozhraní. Konfiguraci vrubu a uložení je na následujícím obrázku.

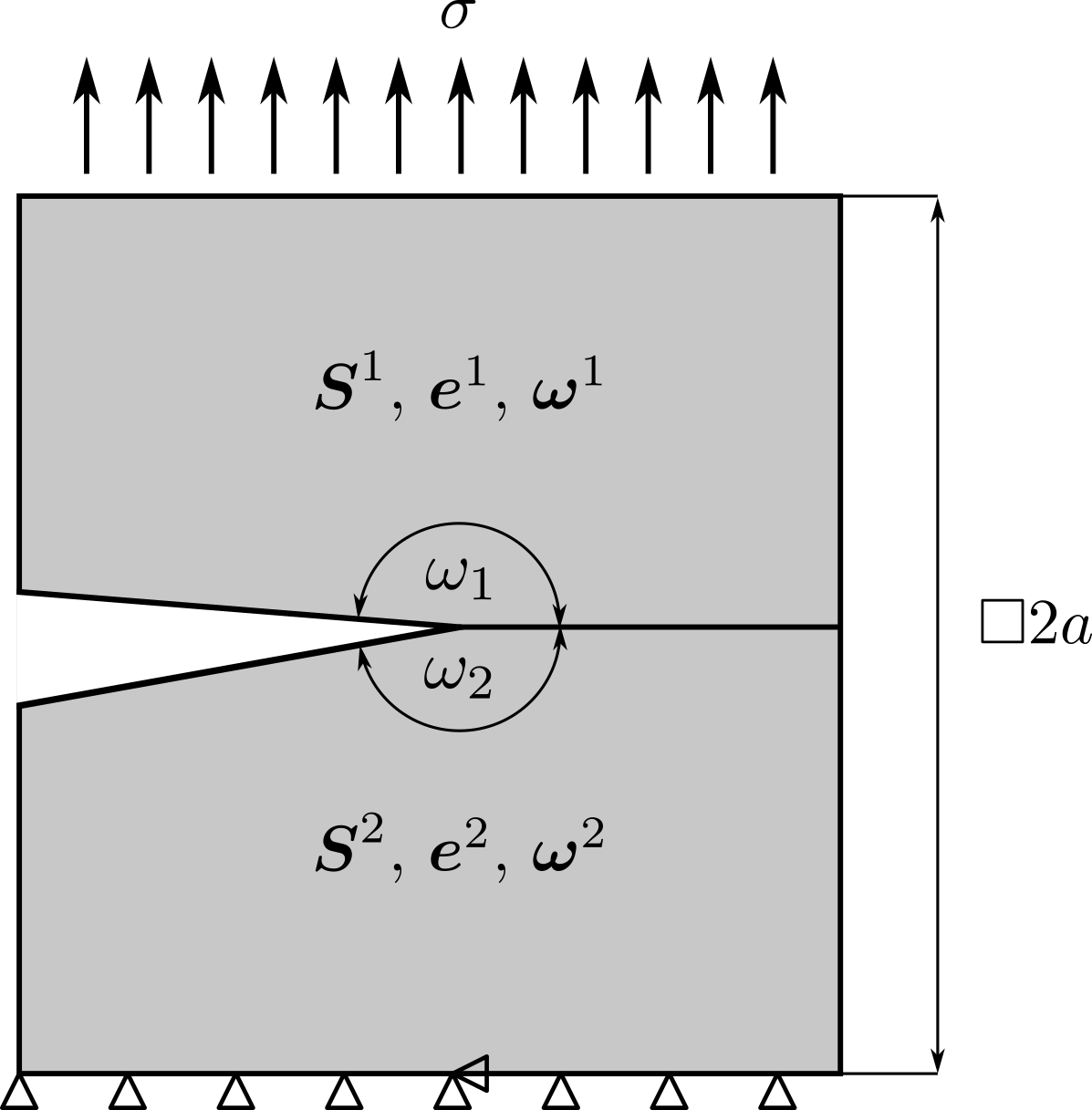
Bimateriálový vrub, PZT-5H s natočením vláken \(90^\circ\) (nahoře), BaTiO3 s natočením vláken taktéž \(90^\circ\) (dole).

Elastické a piezoelektrické konstanty obou materiálů jsou následující.

materiál	PZT-5H
\(C_{11}\)	\(11.7\times 10^{10}\,\mathrm{Pa}\)
\(C_{12}\)	\(5.30\times 10^{10}\,\mathrm{Pa}\)
\(C_{23}\)	\(5.50\times 10^{10}\,\mathrm{Pa}\)
\(C_{22}\)	\(12.6\times 10^{10}\,\mathrm{Pa}\)
\(C_{44}\)	\(3.53\times 10^{10}\,\mathrm{Pa}\)
\(C_{66}\)	\(\big(C_{22}-C_{23}\big)/2\)
\(e_{12}\)	\(-6.50\,\mathrm{C/m^2}\)
\(e_{11}\)	\(23.30\,\mathrm{C/m^2}\)
\(e_{26}\)	\(17.00\,\mathrm{C/m^2}\)
\(\omega_{11}\)	\(13.0\times 10^{-9}\,\mathrm{C/Vm}\)
\(\omega_{22}\)	\(15.1\times 10^{-9}\,\mathrm{C/Vm}\)
\(E_c^\dagger\)	\(8.0\times10^5\,\mathrm{V/m}\)
\(P_0^\dagger\)	\(0.39\,\mathrm{C/m^2}\)

\(^{\dagger)}\) Zdroj: Piezo.com Support.

materiál	BaTiO3
\(C_{11}\)	\(14.6\times 10^{10}\,\mathrm{Pa}\)
\(C_{12}\)	\(6.60\times 10^{10}\,\mathrm{Pa}\)
\(C_{23}\)	\(6.60\times 10^{10}\,\mathrm{Pa}\)
\(C_{22}\)	\(15.0\times 10^{10}\,\mathrm{Pa}\)
\(C_{44}\)	\(4.40\times 10^{10}\,\mathrm{Pa}\)
\(C_{66}\)	\(\big(C_{22}-C_{23}\big)/2\)
\(e_{12}\)	\(-4.35\,\mathrm{C/m^2}\)
\(e_{11}\)	\(17.50\,\mathrm{C/m^2}\)
\(e_{26}\)	\(11.40\,\mathrm{C/m^2}\)
\(\omega_{11}\)	\(11.2\times 10^{-9}\,\mathrm{C/Vm}\)
\(\omega_{22}\)	\(9.87\times 10^{-9}\,\mathrm{C/Vm}\)
\(E_c^\ddagger\)	\(3.5\times10^5\,\mathrm{V/m}\)
\(P_0^\ddagger\)	\(0.07\,\mathrm{C/m^2}\)

\(^{\ddagger)}\) Zdroj: Nagata, K., Kiyota, T. Jpn. J. Appl. Phys. 28 (98), 1989.

Exponenty singularity jsou v další tabulce.

\(\omega_1/\omega_2\)	\(\delta_1\), \(\delta_2\), \(\delta_3\)
\(179^\circ\)/\(-180^\circ\)	\(0.5015\), \(0.5015+0.0135\mathrm{i}\), \(0.5015-0.0135\mathrm{i}\)
\(159^\circ\)/\(-180^\circ\)	\(0.5071\), \(0.5242\), \(0.5669\)

Pro zatížení \(\sigma=1.0\times10^6\,\mathrm{Pa}\) a pro \(\varepsilon_D=5.0\times10^{-3}\) se dostanou následující zóny přepólování.

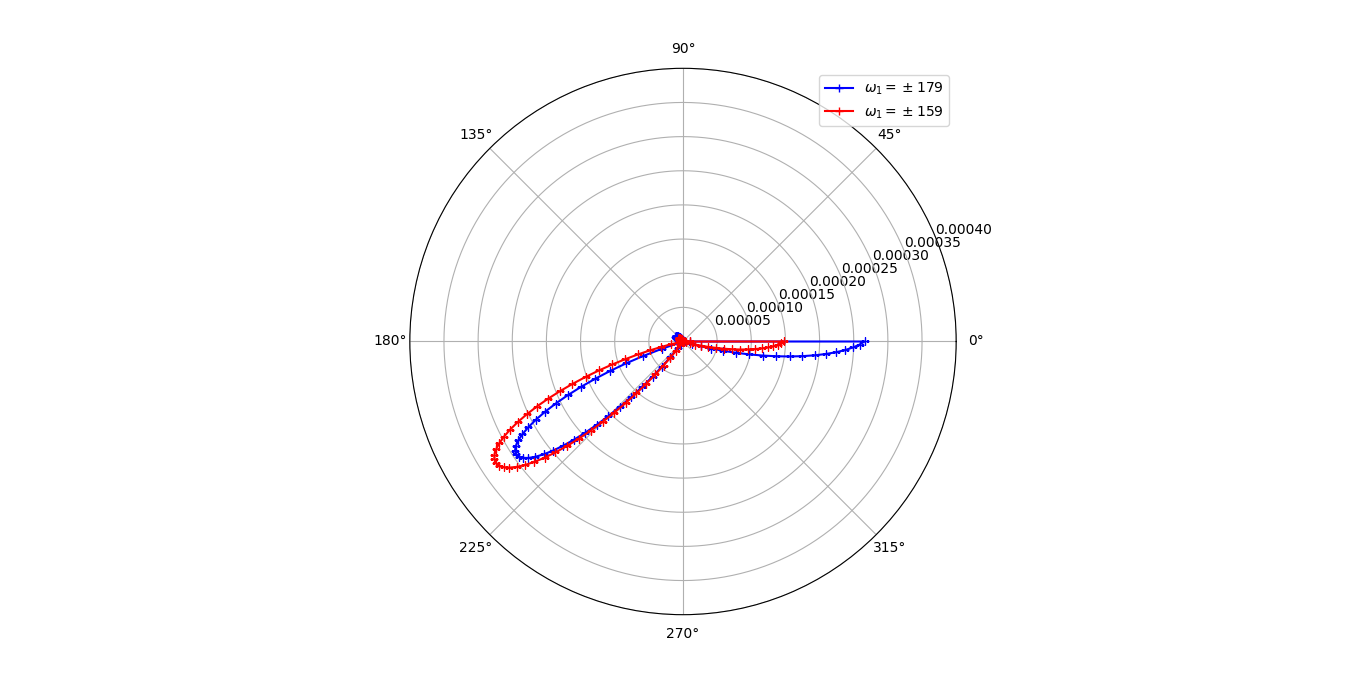
Zóna přepólování bimateriálového vrubu 5ZT-5H/BaTiO3. Jednotky jsou metry.

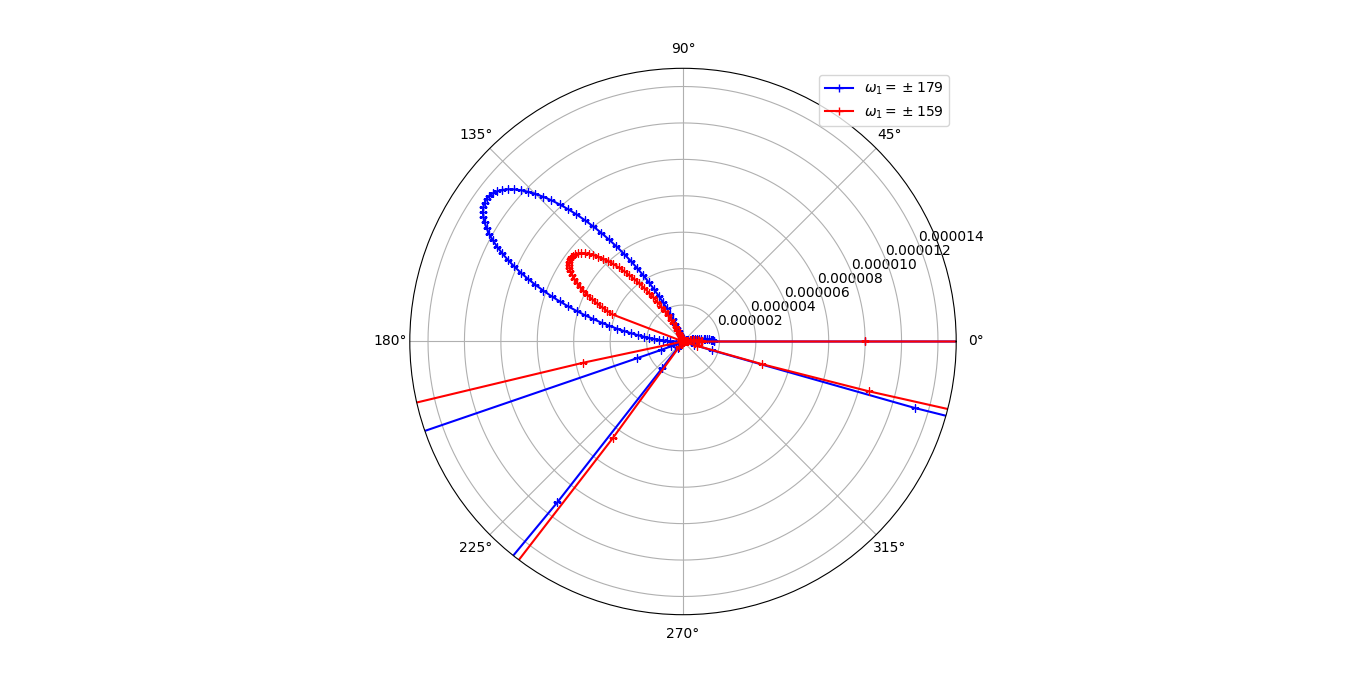
Detail zóny přepólování bimateriálového vrubu 5ZT-5H/BaTiO3. Jednotky jsou metry.

Hodnoty zobecněných součinitelů intenzity napětí ukazuje následující tabulka.

\(\omega_1\)	\(K^{(1)}\,\mathrm{[Pa\times m^{\delta_1}]}\), \(K^{(2)}\,\mathrm{[Pa\times m^{\delta_2}]}\), \(K^{(3)}\,\mathrm{[Pa\times m^{\delta_3}]}\)
\(179^\circ\)	\(1.9094\times10^5\), \(-5.7641\times10^5-3.0103\times10^4\mathrm{i}\), \(-5.2975\times10^5+2.7667\times10^4\mathrm{i}\)
\(159^\circ\)	\(-6.6037\times10^5\), \(4.1799\times10^4\), \(1.1019\times10^5\)

Hraniční křivka zóny přepólování je tvořena úsečkami mezi jednotlivými body křivky, podél kterých se počítá křivkový integrál. Jestliže počáteční a koncový bod každé \(i\)-té úsečky (segmentu) jsou \(A_i\) a \(B_i\), přičemž se samozřejmě koncový a počáteční bod \(B_i\) a \(A_{i+1}\) úseku \(i\) a \(i+1\) navzájem překrývají, pak se integrál (15) podél úseku \(A_iB_i\) spočítá následovně

(16)\[\begin{split}\begin{equation} \begin{split} \Delta K^{(\alpha)} =& \int_{A_i}^{B_i}\Delta\sigma_{ij}h_j^{(\alpha)}(x_1,x_1)n_i\mathrm{d}s \\ =& \int_0^1\Delta\sigma_{ij}h_j^{(\alpha)}(x_1,x_2)n_i \sqrt{\big(x_1^{B_i}-x_1^{A_i}\big)^2+\big(x_2^{B_i}-x_2^{A_i}\big)^2}\mathrm{d}t. \end{split} \end{equation}\end{split}\]

Změny v hodnotách zobecněných součinitelů intenzity napětí z důvodů změny polarizace ve vrcholu vrubu ukazuje poslední tabulka.

\(\omega_1\)	\(\Delta K^{(1)}\,\mathrm{[Pa\times m^{\delta_1}]}\), \(\Delta K^{(2)}\,\mathrm{[Pa\times m^{\delta_2}]}\), \(\Delta K^{(3)}\,\mathrm{[Pa\times m^{\delta_3}]}\)
\(179^\circ\)	\(1.6308\times10^5\), \(-1.5089\times10^5-2.1334\times10^5\mathrm{i}\), \(-1.3868\times10^5+1.9607\times10^5\mathrm{i}\)
\(159^\circ\)	\(-1.7669\times10^5\), \(7.8342\times10^4\), \(6.7523\times10^5\)

Použité skripty

• binotch_piezo.py - základní pythonovský skript pro výpočet zobecněných součinitelů intenzity napětí a jejich změn, výpočet pro stanovení zóny přepólování.

• binotch_piezo_gmsh.py - pythonovský skript, který vytvoří a zkompiluje *.geo soubor a vytvoří konečnoprvkovou síť.

• binotch_piezo_FEniCS.py - pythonovský skript pro konečnoprvkové výpočty ve FEniCSu.

• switch_zone_plot.py - pythonovský skript pro vykresleni zóny přepólování.

• mod_LES_Mirek2.py, mod_HSV_v4.py - nutné pythonovské moduly s procedurami pro výpočet zobecněných součinitelů intenzity napětí, jejich změn vlivem přepólováním a stanovení zóny přepólování.

Literatura

[1] (1,2,3,4)

Hrstka, M., Evaluation of Fracture Mechanical Parameters for Bi-Piezo-Material Notch, Dizertační práce, FSI VUT v Brně, 2019.

[2] (1,2,3,4)

Hrstka, M., Profant, T., Kotoul, M., Electro-mechanical singularities of piezoelectric bi-material notches and cracks, Engineering Fracture Mechanics, 2019, https://doi.org/10.1016/j.engfracmech.2019.05.016.

[3] (1,2)

Ricoeur, A., Kuna, M., Influence of electric fields on the fracture of ferroelectric ceramics, Journal of the European Ceramic Society, 23, 1313–1328, 2003.

[4]

Zhu, T., Yang, W., Toughness variation of ferroelectrics by polarization switch under non-uniform electric field. Acta mater., 45 (11), 4695-4702, 1997.

[5]

Rajapakse, R.K.N.D., Zeng, X., Toughening of conducting cracks due to domain switching. Acta mater., 49, 877–885, 2001.

[6]

Belov, A.Y., Kirchner, H.O.K., Universal wieght functions for elastically anisotropic angularly inhomogenous media with notches or cracks. Philosophical Magazine A, 73 (6), 1621-1646.