Výuka - dodatek II

Metoda hraničních prvků - ELBECON

Metoda hraničních integrálních rovnic (BIE) je nejjednodušší forma metody hraničních prvků. Zde je ukázka její aplikace včetně jednoduchých skriptů v Pythonu a Fortranu. Skripty vychází z programu ELBECON publikovaném v knize [1]. Program je modifikován na případ rozdělení tělesa na dvě podoblasti, případně pro modelování bimateriálu. Trocha teorie a odkazy na další literaturu lze nalézt v diplomové práci [2]. Ve formátu pdf si ji lze stáhnout zde. Níže uvedené skripty vyžadují GMSH mesh generator, Python a jeho knihovny matplotlib a numpy. Všechny tyto programy jsou součástí tzv. svobodného softwaru a mohou se volně stahovat a instalovat. Způsob instalace závisí pouze na operačním systému, na kterém budou pracovat.

Linux

Program GMSH by měl být součástí instalačních balíčků. Python je přímo součástí systému. Knihovna numpy a matplotlib je také součástí instalačních balíčků. Je nutné ještě zkontrolovat, zda jsou nainstalovány balíčky python-dev a gfortran, nutné ke správnému průběhu kompilace fortranovských kódů.

Windows

Program GMSH lze stáhnout na gmsh.info. Sympatická distribuce Pythonu s knihovnami matplotlib a numpy je Continuum Analytics - Anaconda, stáhnout ji lze na www.anaconda.com.

Jádrem pythonovských skriptů je fortranovský kód v modulu BIE.f90, který je možné stáhnout zde. Je však nutné ho zkompilovat příkazem f2py -c BIE.f90 -m bie. Je nutné dodržet velikost písmen. V Linuxu se příkaz provede jednoduše v okně terminálu a samozřejmě v adresáři, kde se nachází soubor BIE.f90. Vznikne soubor bie.so, který je modulem Pythonu a může se z něj také volat. Ve Windows je nutné v Anacondě spustit promt commander a v adresáři se souborem BIE.f90 provést výše zmíněný příkaz. Vznikne soubor bie.pyd, který je pythonovským modulem. Moduly m_prepBIE.py a m_procBIE.py lze stáhnout zde a zde. Fortranovský modul BIE.f90 lze stáhnout zde.

Příklad 1

Případ přímého prutu zatíženého na hranici 4 napětím \(\sigma_{yx}=-100\,\mathrm{MPa}\) a na hranici 8 je vetknut. Materiál je \(E=2.1\times10^5\,\mathrm{MPa}\) a \(\nu=0.3\). Potřebné soubory ke stažení jsou gmsh_prut.geo, gmsh_prut.msh a prut.py.

Geometrie úlohy v programu GMSH je následující.

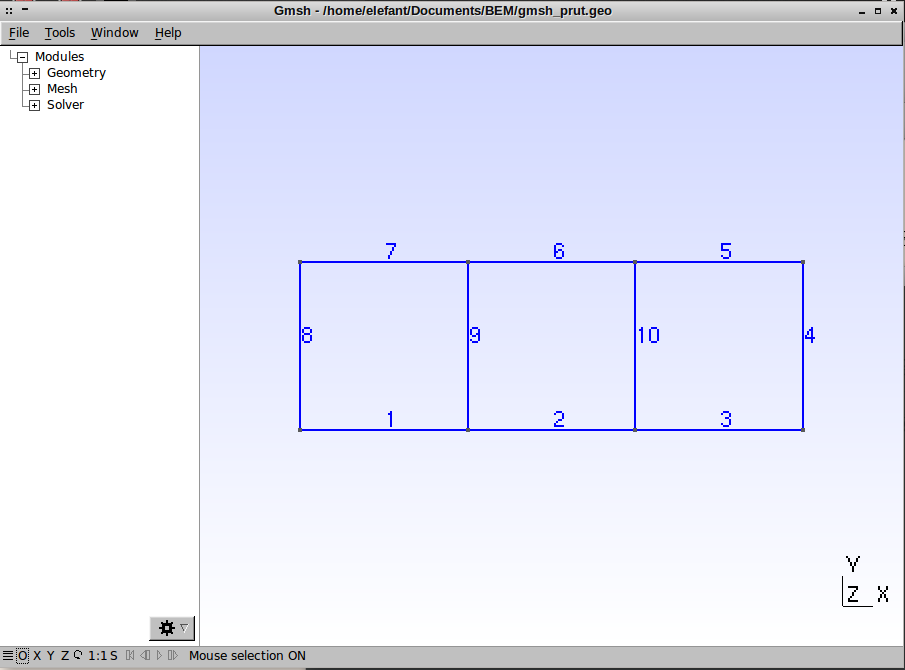
Rozložení posuvů a napětí v prutu ukazují následující grafy.

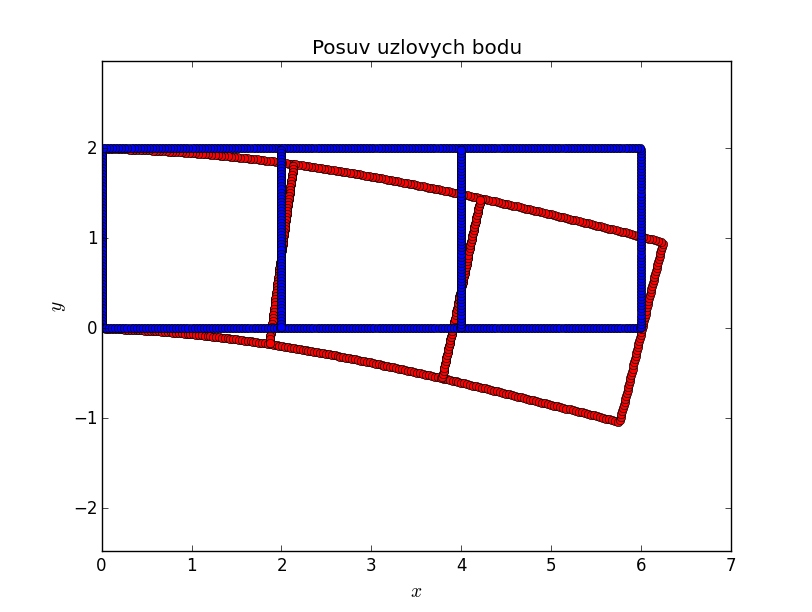
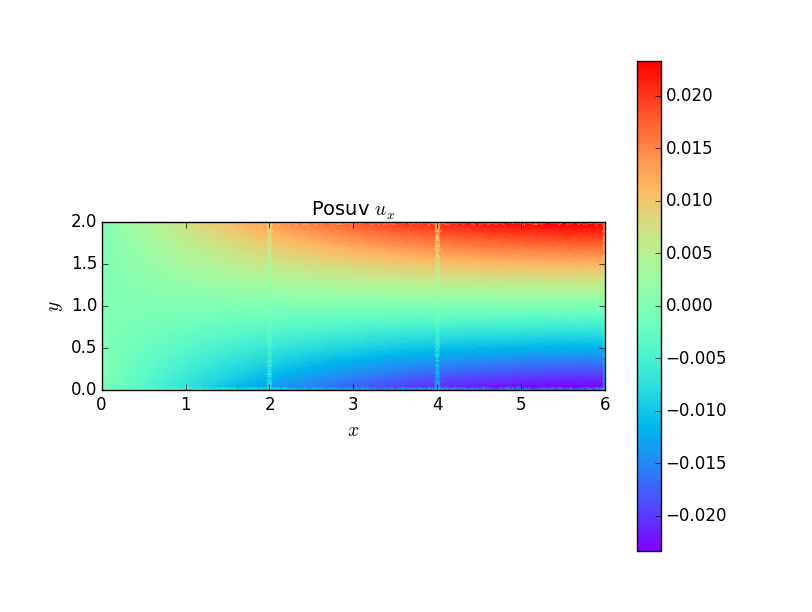
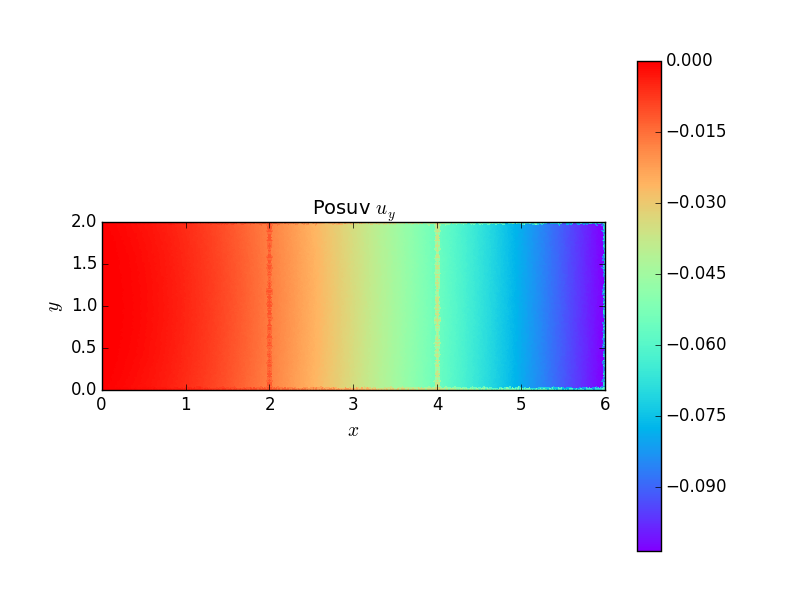
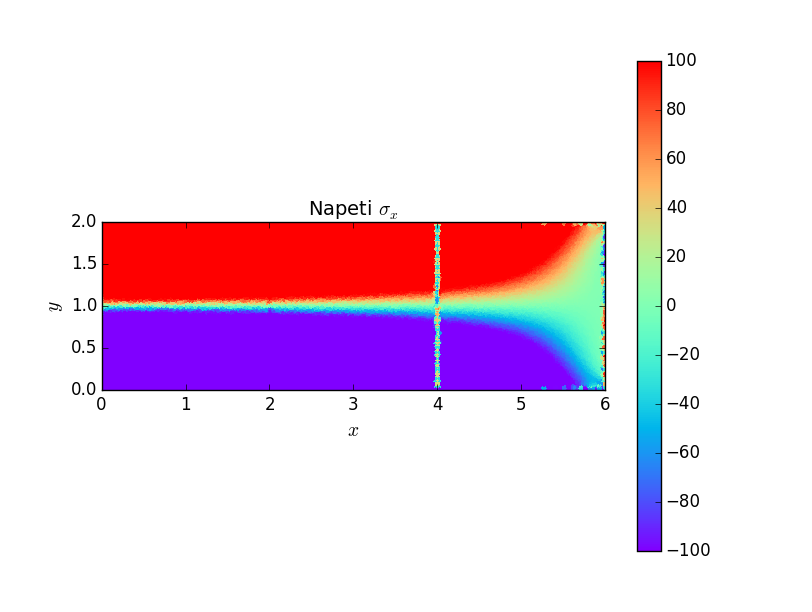
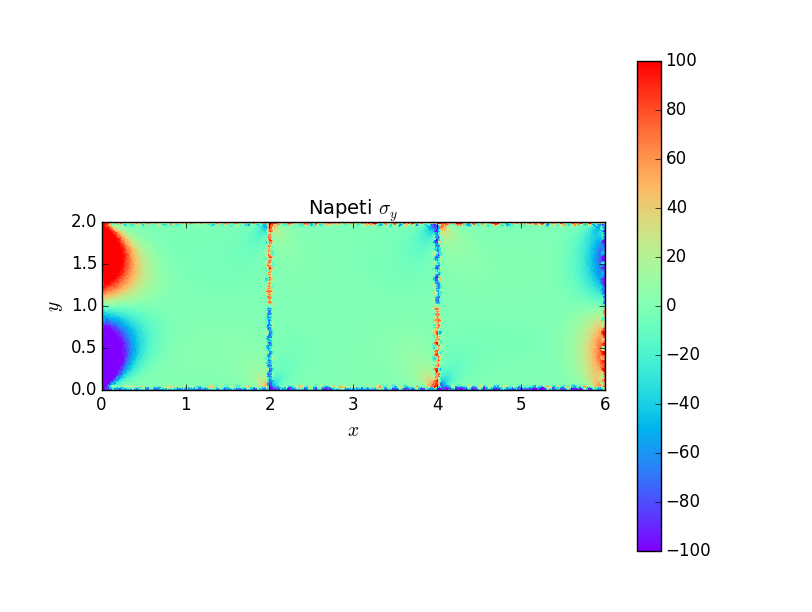
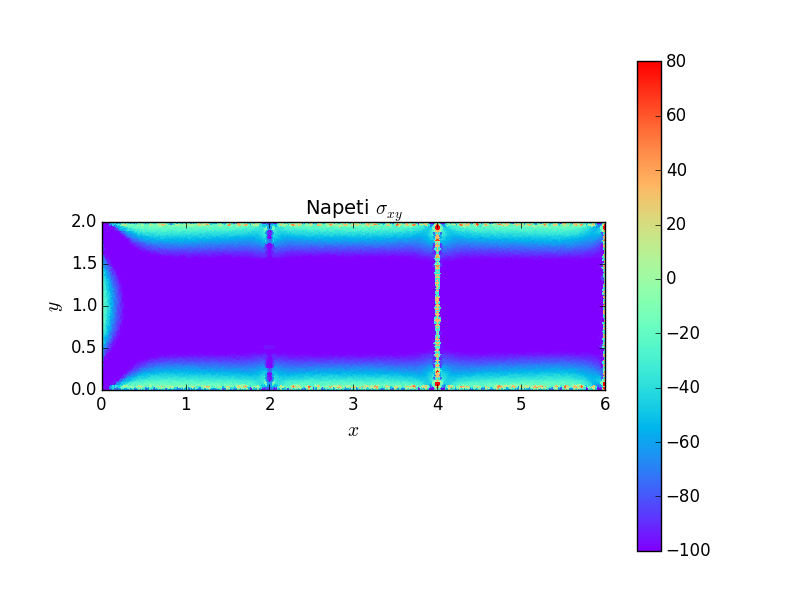
Příklad 2

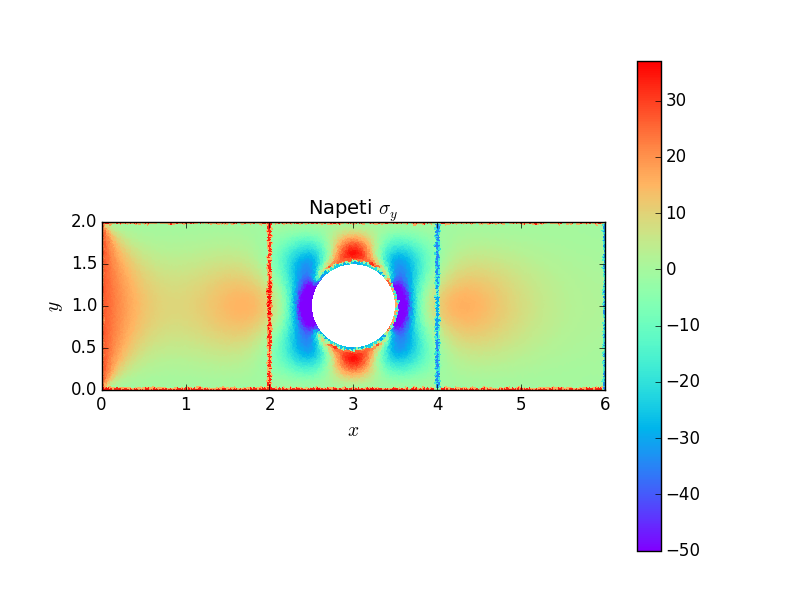
Případ přímého prutu s otvorem zatíženého na hranici 4 napětím \(\sigma_{yx}=-100\,\mathrm{MPa}\) a na hranici 8 je vetknut. Materiál je \(E=2.1\times10^5\,\mathrm{MPa}\) a \(\nu=0.3\). Potřebné soubory ke stažení jsou gmsh_prut_otvor.geo, gmsh_prut_otvor.msh a prut_otvor.py.

Geometrie úlohy v programu GMSH vypadá následovně.

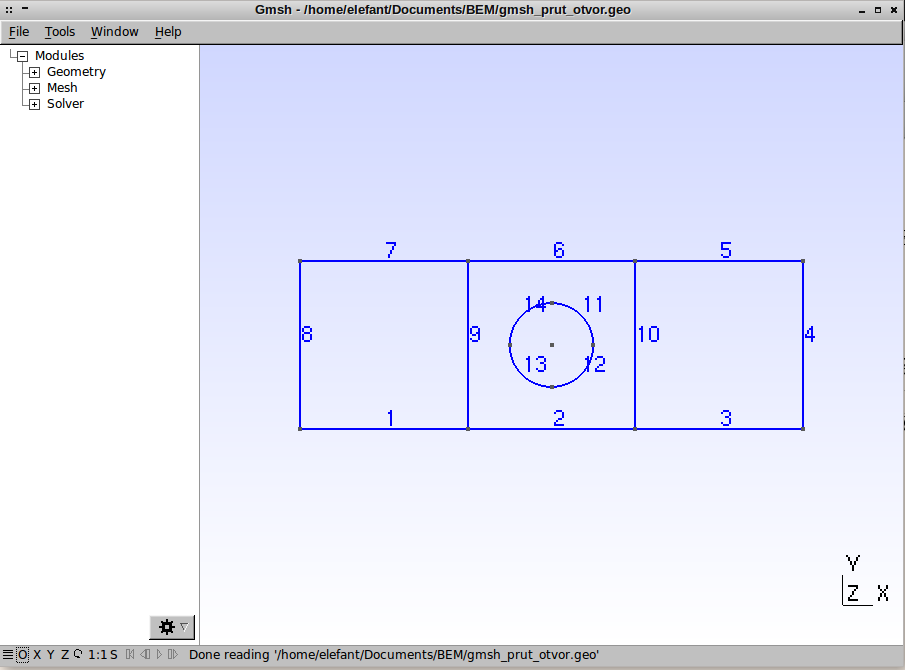
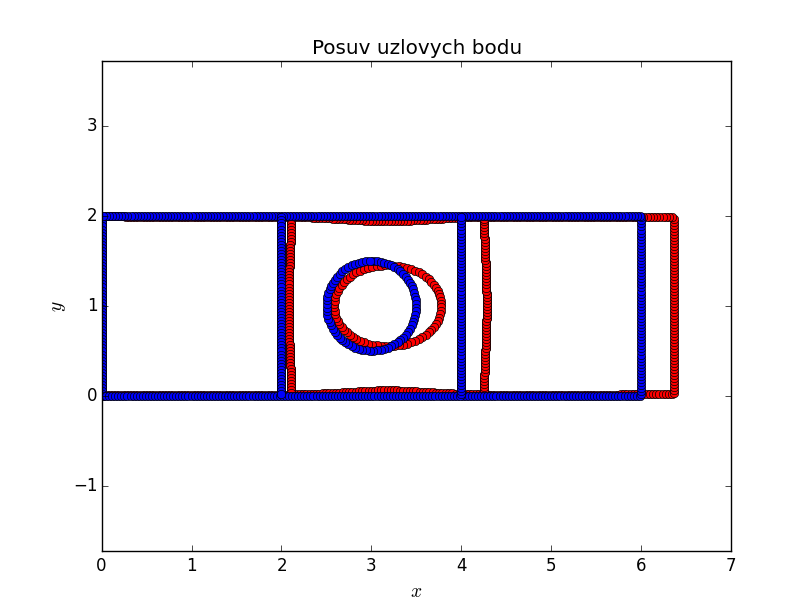
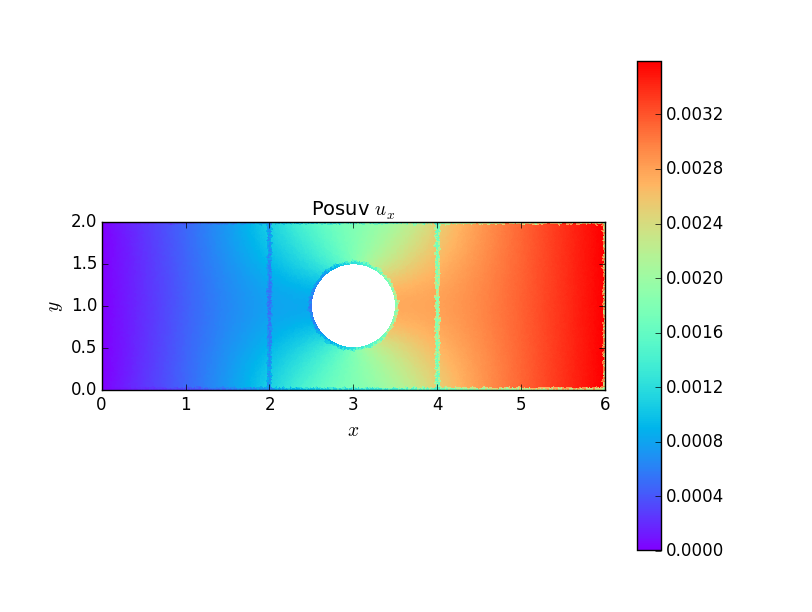
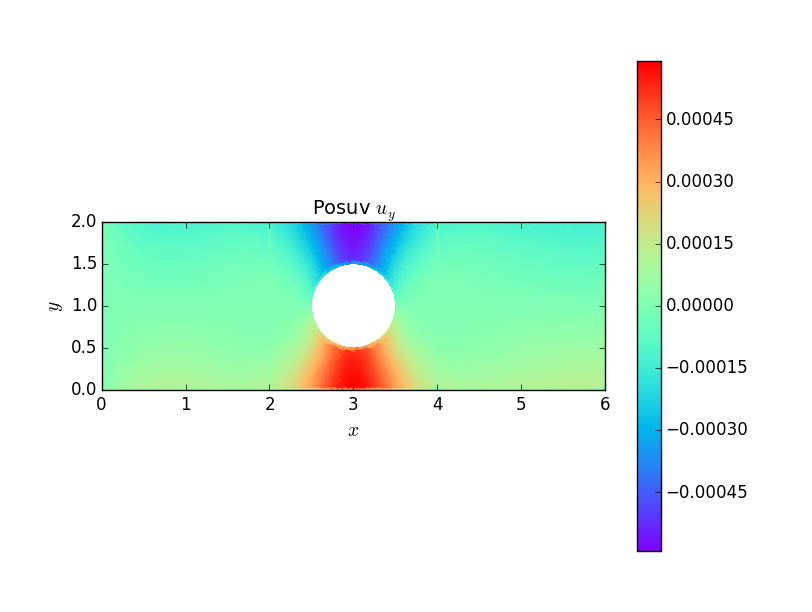
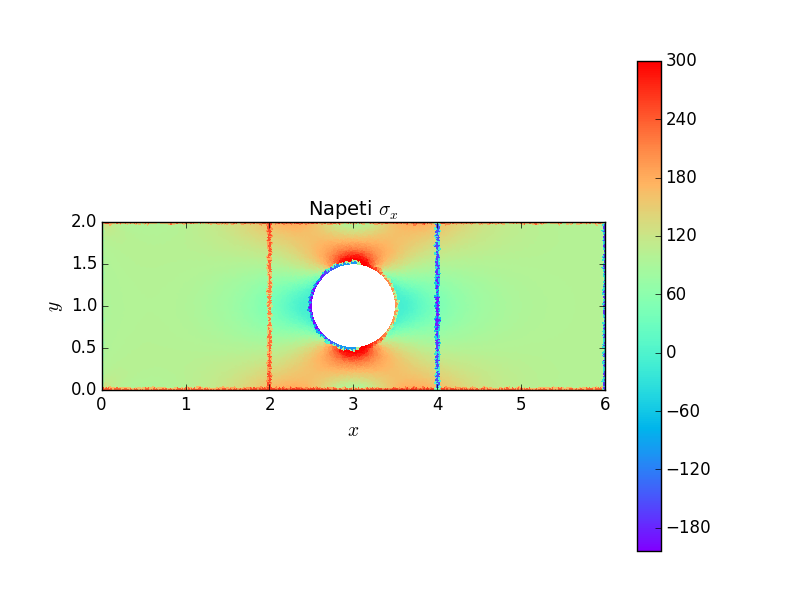
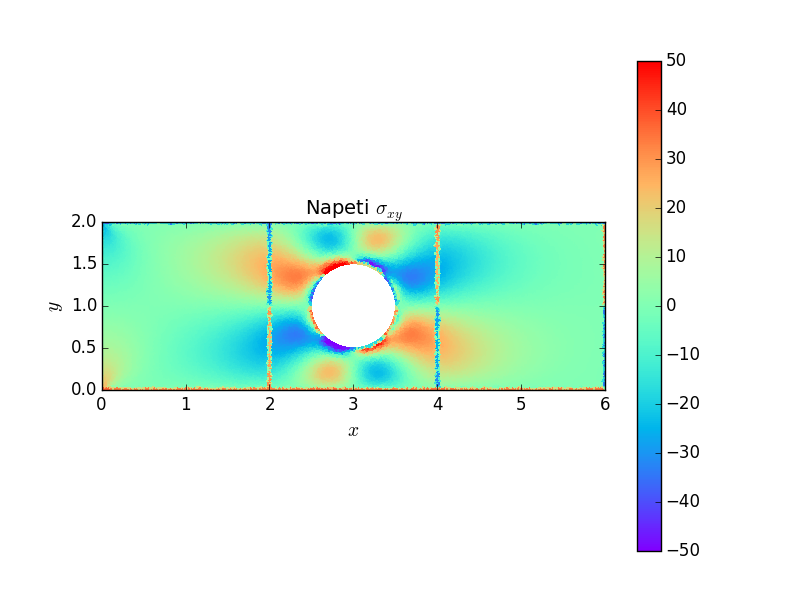
Následují grafické výstupy posuvů a napětí v součásti. Je důležité si povšimnou, že otvor způsobuje koncentraci napětí \(\sigma_x\) \(1.5\times\) větší než napětí nominální, na rozdíl od trhliny nebo ostrého vrubu, kde napětí roste nad všechny meze. Avšak otvor způsobuje koncentraci napětí na větší oblasti, opět na rozdíl od trhliny a ostrého vrubu, kde je koncentrace napětí lokální záležitostí.

Příklad 3

Případ přímého prutu s osazením a zatíženého na hranici 6 napětím \(\sigma_x=100\,\mathrm{MPa}\) a vetknutím na hranici 12. Materiál prutu je \(E=2.1\times10^5\,\mathrm{MPa}\) a \(\nu=0.3\). Cílem je zjistit hodnoty napětí ve vrubu jehož geometrické parametry jsou,

(1)\[\frac{r}{D}=\frac{1}{20}=0.05,\quad\frac{d}{D}=\frac{4}{5}=0.8.\]

Z této geometrie vrubu vychází součinitel koncentrace napětí \(\alpha\approx 1.6\). Potřebné soubory k řešení úlohy jsou gmsh_prut_vrub.geo, gmsh_prut_vrub.msh a prut_vrub.py.

Geometrie prutu je v programu GMSH následující,

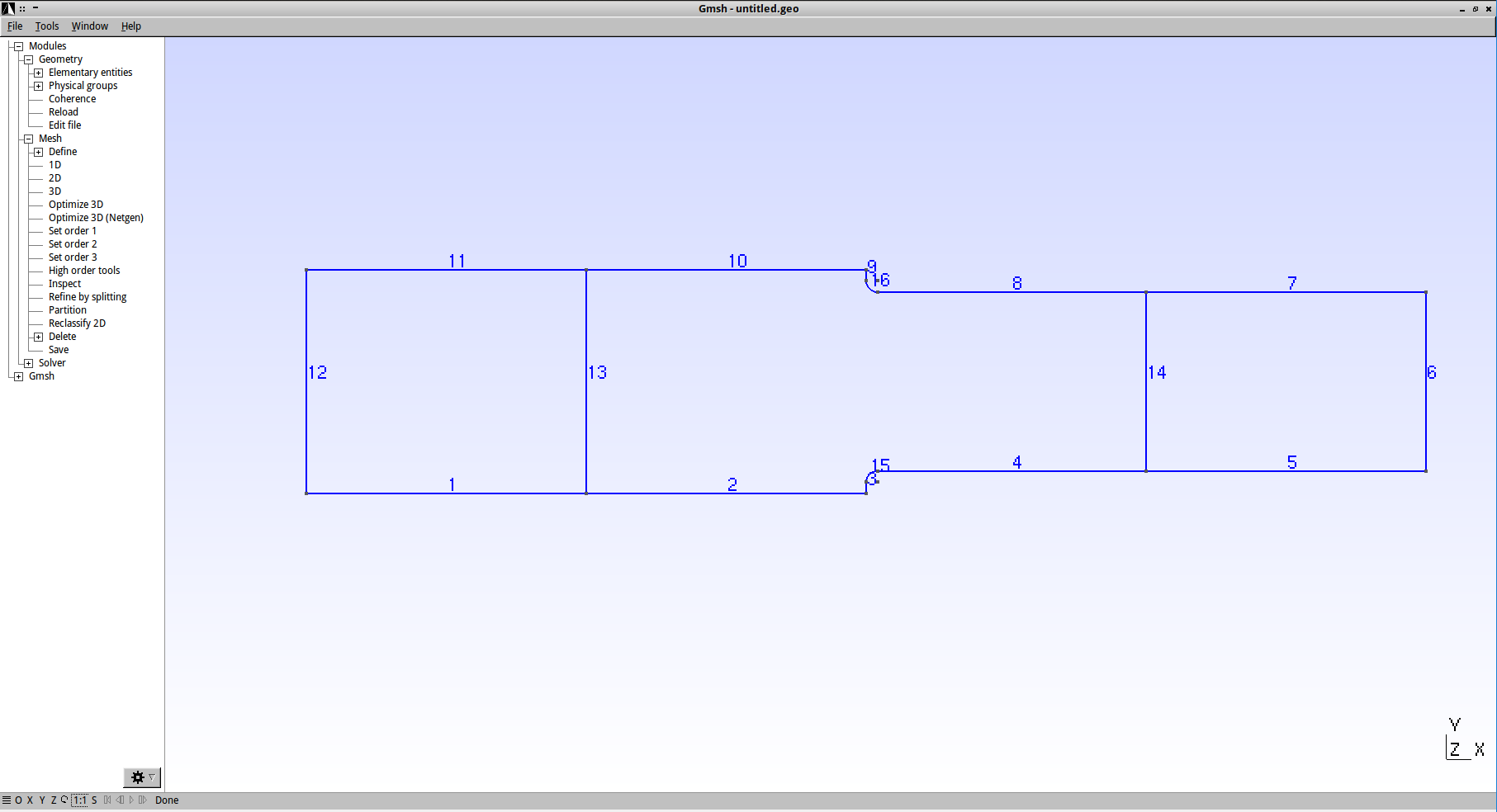
Následující grafy ukazují posuvy a koncentraci napětí v místě začátku změny průřezu užší části prutu vlivem zaoblení kořene vrubu. Jde dobře vidět lokální charakter koncentrace napětí.

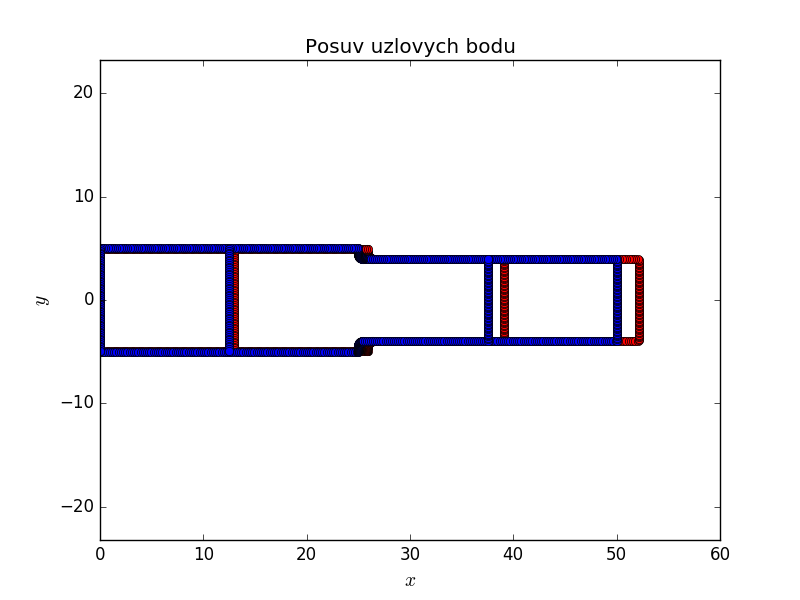
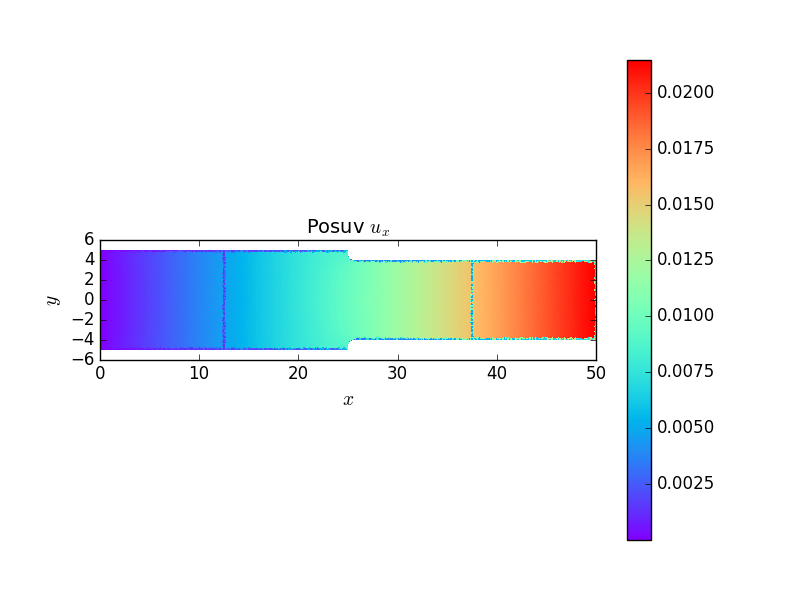
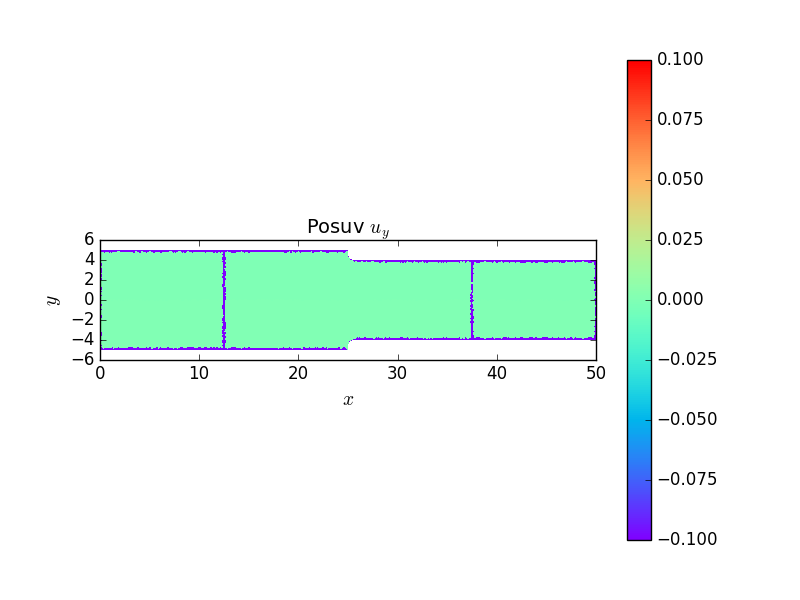
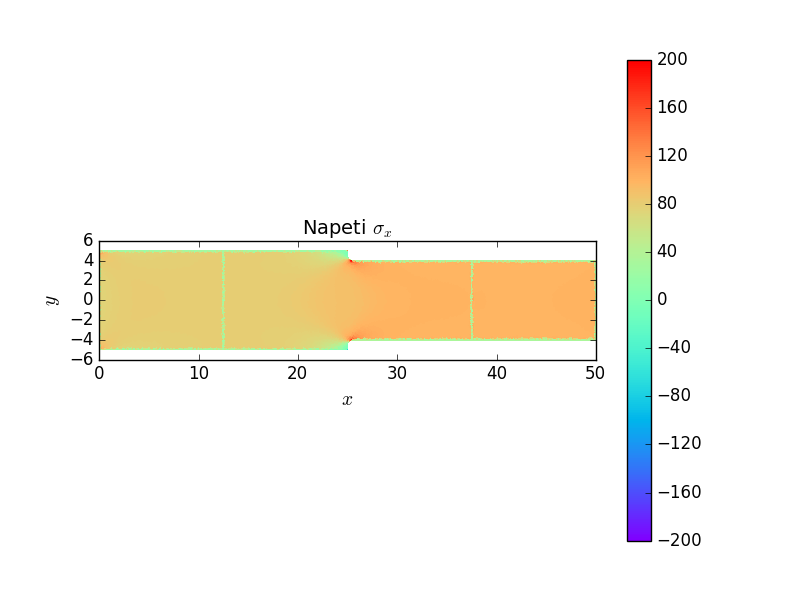
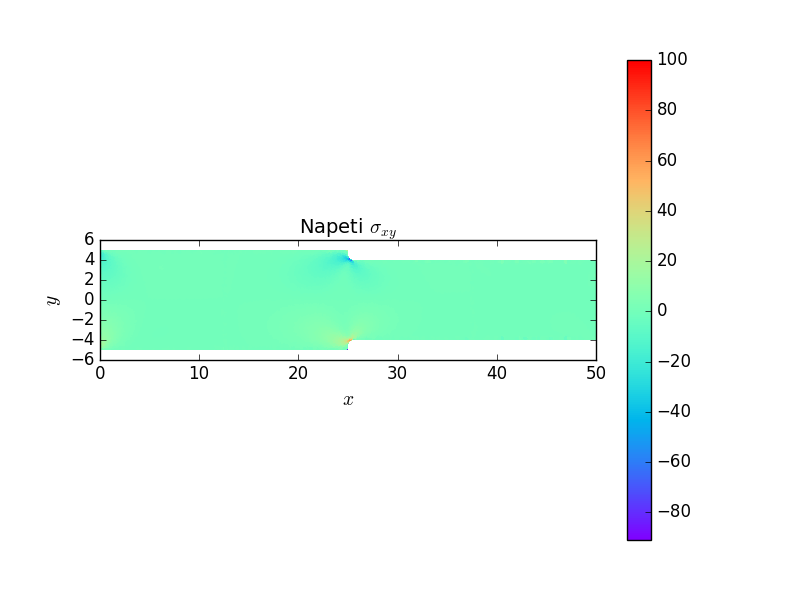
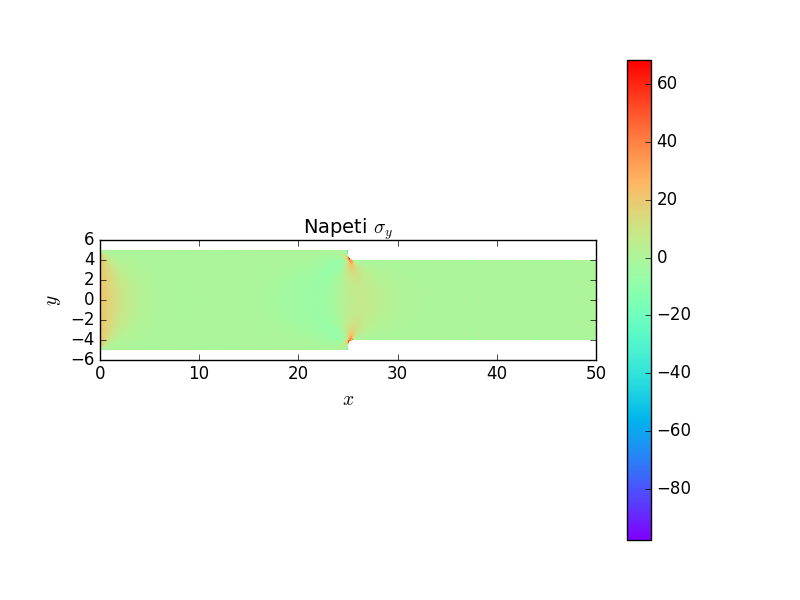
Poslední graf ukazuje průběh napětí \(\sigma_x\) v průřezu \(x=b+r\), který odpovídá místu, kde dochází k zvětšování příčného průřezu vlivem poloměru kořene vrubu. Z grafu vychází součinitel koncentrace napětí \(\alpha\approx1.6\).

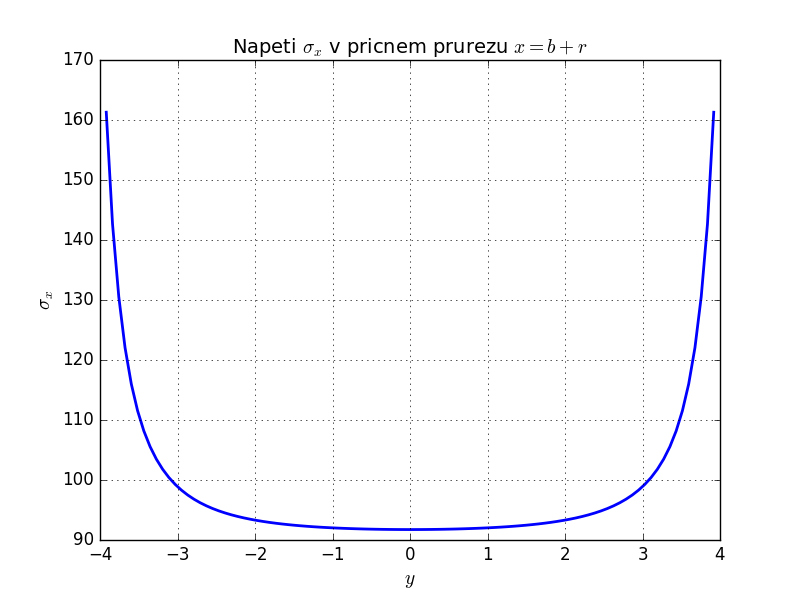
Příklad 4

Případ bi-materiálového pravoúhlého vrubu zatíženého na hranici 5 napětím \(\sigma_y=100\,\mathrm{MPa}\) a na hranicích 1 a 7 je vetknut. Materiál je \(E_1=2.1\times10^5\,\mathrm{MPa}\), \(E_2=1.5\times10^5\,\mathrm{MPa}\) a \(\nu_{1,2}=0.3\). Potřebné soubory ke stažení jsou gmsh_bi-vrub.geo, gmsh_bi-vrub.msh a bi-vrub.py.

Geometrie vrubu je v programu GMSH následující,

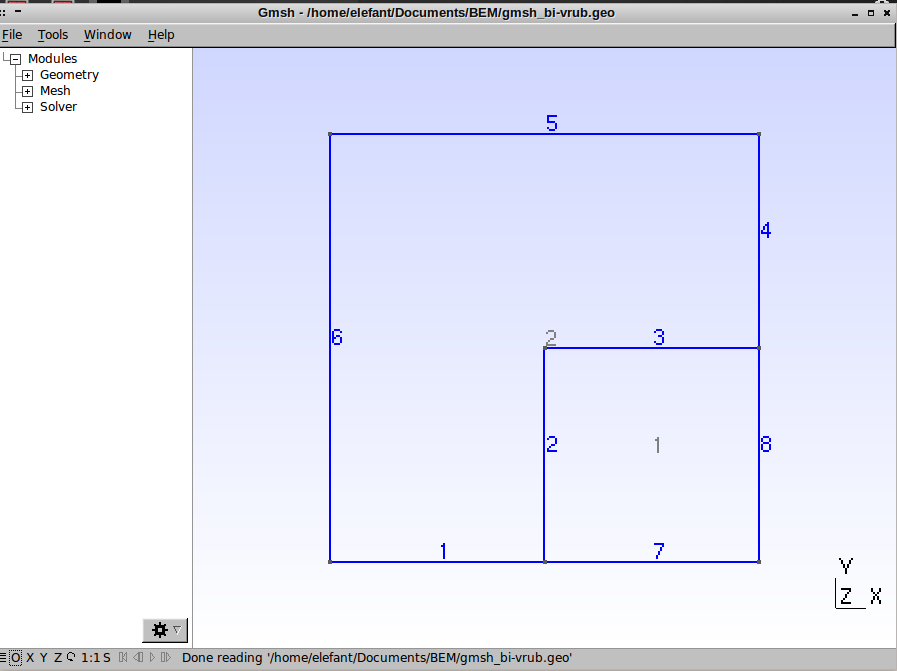
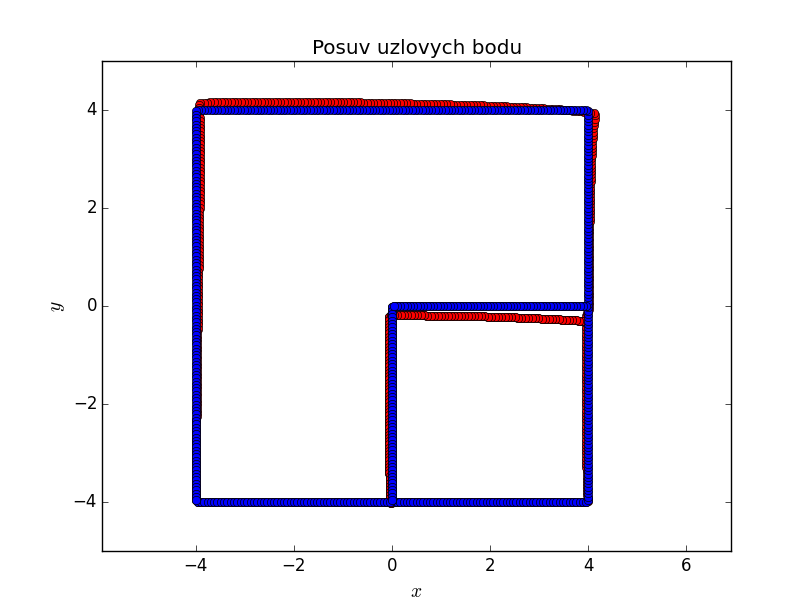
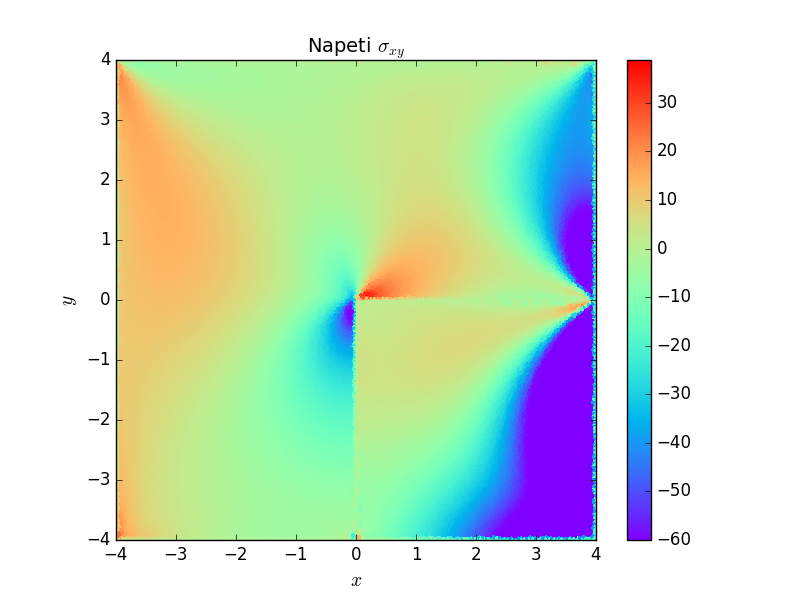
Následující grafy posuvů a napětí ukazují, jak se bi-materiálová rozhraní chovají jako koncentrátory. Zajímavý je \(180\)-ti stupňový bi-materiálový vrub na pravé hranici. I když na první pohled se nejedná o vrub, ale přímou hranici, rozdílné elastické vlastnosti bi-materiálu se projevují koncentrací napětí.

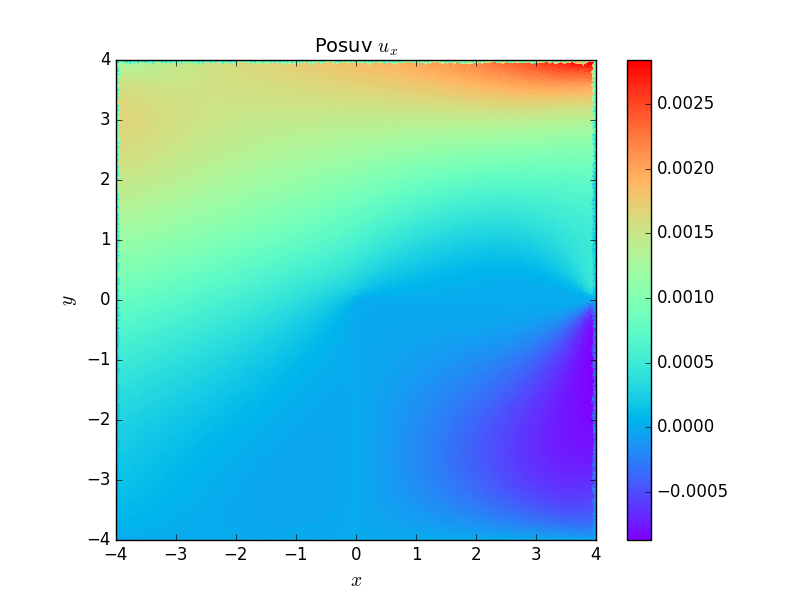
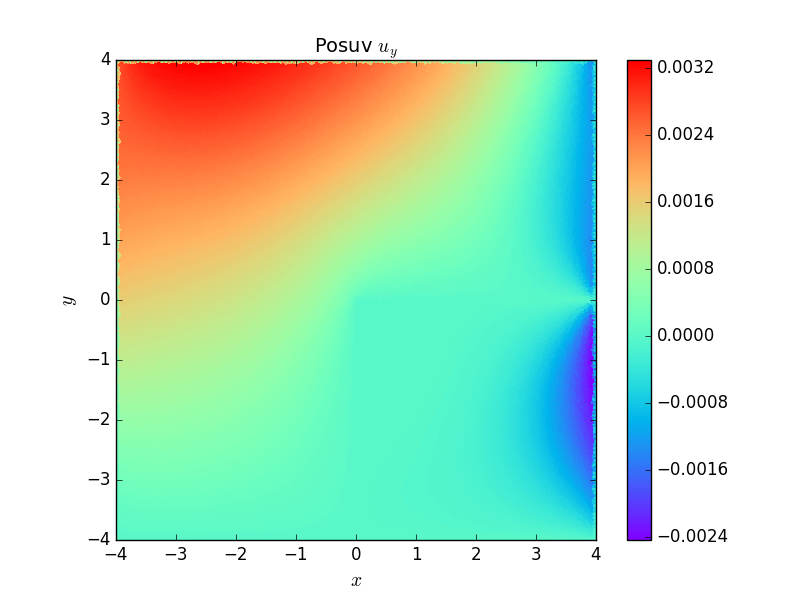
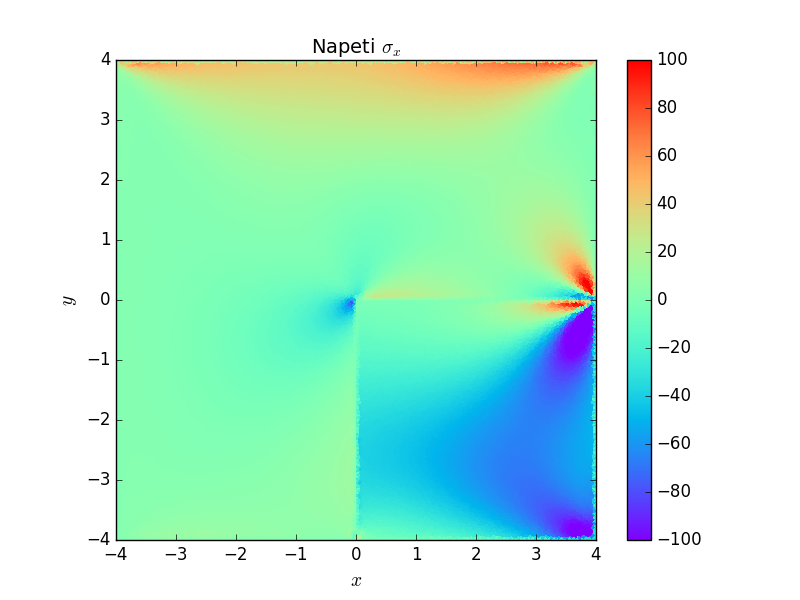
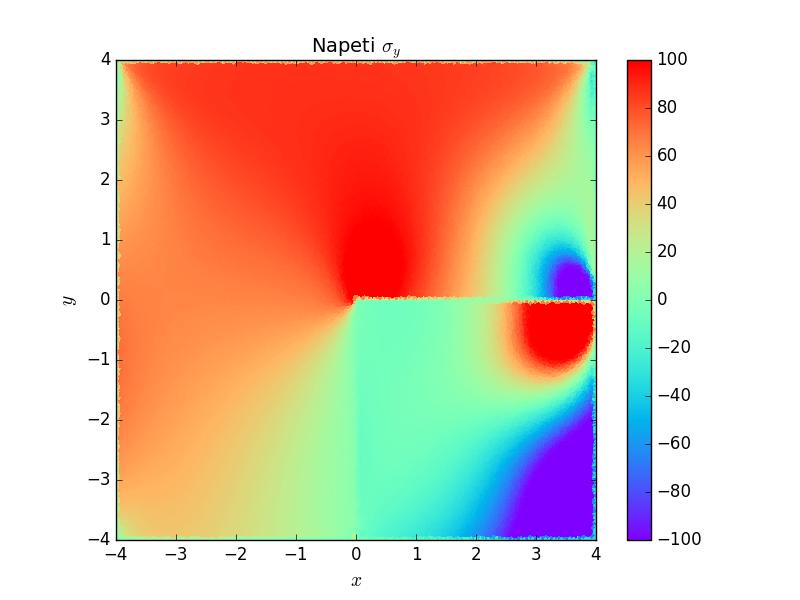
Literatura

[1]

Katsikadelis, J.T., 2003, Boundary Elements: Theory and Applications. Elsevier.

[2]

Sedláček, S., 2012, Aplikace metody hraničních prvků na některé problémy trhliny v blízkosti bimateriálového rozhraní. Diplomová práce, Vutium, Brno.

Metoda konečných prvků - FreeFEM++

FreeFEM++ je volně dostupný konečnoprvkový software. Je podobně jako FEniCS specifický způsobem formulování řešené úlohy pomocí vlastního skriptovacího jazyka vycházejícího ze syntaxe C++, ve kterém se samozřejmě příkazy jazyka C++ mohou přímo použít. Potřebné informace o projektu FreeFEM++ lze nalézt na stránkách projektu freefem.org. Níže jsou ukázky použití FreeFEM++ pro některé úlohy ze základního studia pružnosti a pevnosti. První úloha aplikuje Poissonovu rovnici na případ prostého krutu prizmatického prutu profilu L. Druhá úloha řeší Laplaceovu rovnici a její aplikaci na průhyb membrány eliptického tvaru a konečně třetí úloha řeší případ teplotně zatíženého bi-materiálového prutu. FreeFEM++ má implementovaný zajímavý nástroj pro tvorbu konečnoprvkové sítě, dokáže však stejně jako FEniCS zpracovat konečnoprvkové sítě vytvořené externími programy, např. gmsh.info. FreeFEM dokáže vygenerovat výstupy v celé řadě formátů, explicitně v PostScriptu pomocí programu gnuplot.info. Jde o jeden z klíčových, průkopnických a volně dostupných programů pro generování grafů. Další podporovaný formát je formát vtu pro volně dostupný software paraview.org, který dokáže zpracovávat a vizualizovat data ve 2D i 3D.

Prostý krut prizmatického prutu s nekruhovým příčným průřezem (FreeFEM++ v4.2.1)

Prostý krut prizmatických prutů s nekruhovým příčným průřezem je aplikací Lapceovy a Poissonovy rovnice v pružnosti a pevnosti. Tyto rovnice lze analyticky řešit pouze pro příčné průřezy velmi jednoduchých tvarů a za přispění dodatečných zjednodušujících předpokladů. V obecném případě musí být použita některá ze známých numerických metod, např. metody konečných prvků. Úloha je anti-rovinná analogická úloze o průhybu membrány. Jestliže je příčný průřez definovaný v rovině \(xy\) a osa podélná osa prutu je rovnoběžná s osou \(z\), pak pro posuvy platí

(2)\[\begin{split}\begin{equation} \begin{split} u_x &= -\theta yz, \\ u_y &= \theta xz, \\ u_z &= \theta w, \end{split} \end{equation}\end{split}\]

kde \(w\equiv w(x,y)\) je deplanační funkce závisející na souřadnicích \(x\) a \(y\) a která musí vyhovovat tzv. Laplaceově rovnici

(3)\[\Delta w=0\quad\mathrm{na}\ \Omega,\]

s tzv. Neumannovými okrajovými podmínkami

(4)\[\partial_n w=-xn_y+yn_x\quad\mathrm{na}\ \partial\Omega.\]

Symboly \(\Omega\) a \(\partial\Omega\) značí příčný průřez a jeho hranici s vnější normálou \(\boldsymbol{n}=(n_x,n_y)\) a pro \(\theta\) platí

(5)\[\theta=\frac{\mathcal{M}_k}{GJ},\]

kde \(\mathcal{M}_k\) je vnější kroutící moment, \(G\) je modul pružnosti ve smyku a \(J\) je modifikovaný polární moment plochy

(6)\[J=\int_\Omega\big(x^2+y^2\big)\mathrm{d}\Omega-\int_\Omega\big(y\partial_x w-x\partial_yw\big)\mathrm{d}\Omega.\]

Jediné nenulové složky napětí jsou \(\sigma_{zx}\) a \(\sigma_{zy}\), které je samozřejmě možné vyjádřit z Hookeova zákona a vztahů (2). Další možností a z numerického hlediska přesnější je využít tzv. Prandtlovy funkce napětí \(\chi\equiv\chi(x,y)\), pro kterou platí

(7)\[\begin{split}\begin{equation} \begin{split} \Delta\chi =& 2\quad\mathrm{na}\ \Omega \\ \chi =& 0\quad\mathrm{na}\ \partial\Omega. \end{split} \end{equation}\end{split}\]

a

(8)\[\sigma_{zx}=-G\theta\partial_y\chi,\quad\sigma_{zy}=G\theta\partial_x\chi.\]

Rovnice (7) jsou tzv. Poissonova rovnice a homogenní Dirichletova okrajová podmínka. Pomocí Prandtlovy funkce se může vypočítat modifikovaný polární moment plochy

(9)\[J=2\int_\Omega\chi\mathrm{d}\Omega.\]

Bez dalších podrobností si uvedeme slabou formulaci obou výše uvedených parciálních diferenciálních rovnic, jejíž znalost je nutná pro aplikaci v konečnoprvkovém systému FreeFEM++

(10)\[\int_\Omega\nabla w\cdot\nabla v\mathrm{d}\Omega=-\int_{\partial\Omega}\partial_n w\mathrm{d}\Omega\]

a

(11)\[\int_\Omega\nabla\chi\cdot\nabla v\mathrm{d}\Omega=\int_\Omega 2v\mathrm{d}\Omega, \qquad \chi=0\quad\mathrm{na}\ \partial\Omega,\]

kde \(v\) je libovolná funkce z jistého prostoru konečných prvků definovaných na diskretizované oblasti \(\Omega\).

Formulace problému

Cílem je vyjádřit rozložení napětí a posuvů v příčném průřezu tvaru L prizmatického prutu namáhaného prostým krutem. Příčný průřez je definován v rovině \(xy\), přičemž výška a šířka profilu jsou \(h=10\,\mathrm{mm}\) a \(b=5\,\mathrm{mm}\). Vektor kroutícího momentu leží ve směru podélné osy prutu, tj. ve směru kladné osy \(z\) a má velikost \(\mathcal{M}_k=1\times 10^3\,\mathrm{Nmm}\). Materiál prutu je ocel \(E=2.1\times 10^5\,\mathrm{MPa}\), \(\nu=0.3\).

Řešení

Skript pro FreeFEM++ lze stáhnout zde, jehož výstupy jsou na následujících obrázcích.

Hranice oblasti \(\Omega\) ve tvaru profilu L. Šipky značí orientaci hranice \(\partial\Omega\), přičemž oblast \(\Omega\) leží na levé straně orientované hranice \(\partial\Omega\).

Konečnoprvková síť oblasti \(\Omega\).

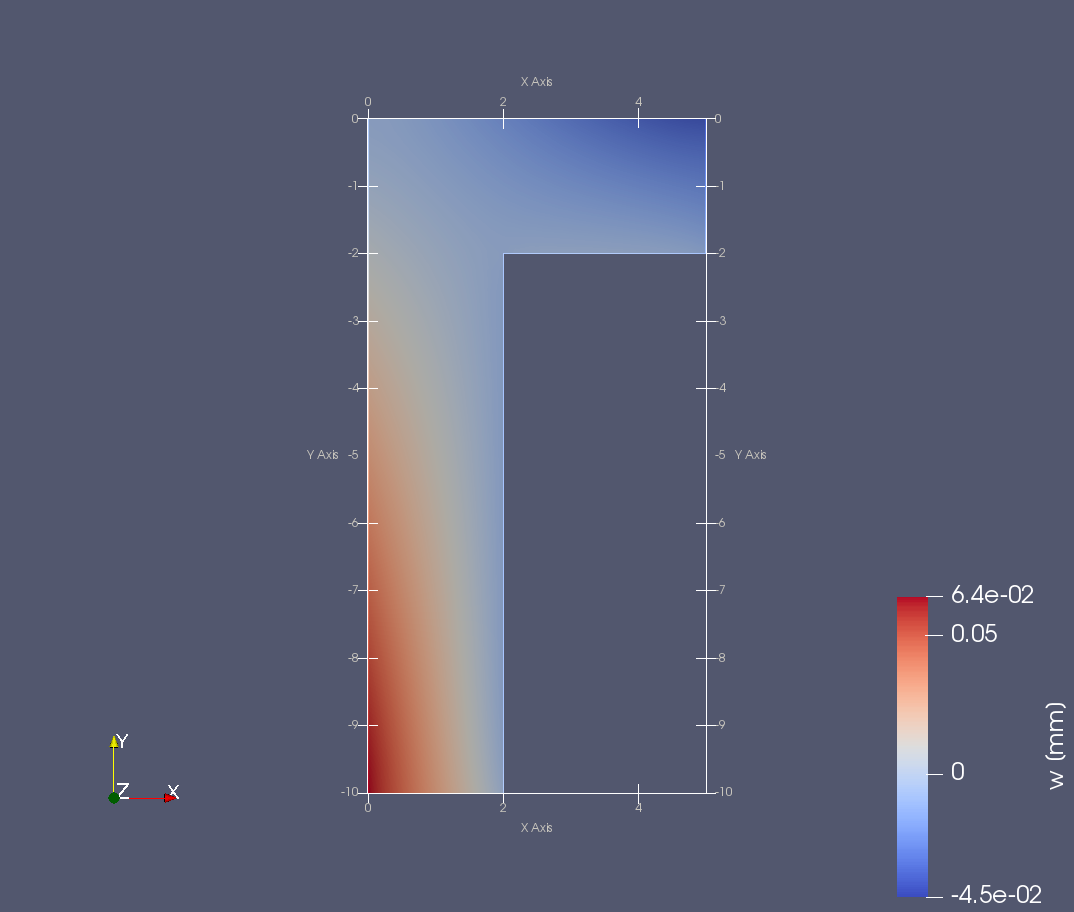
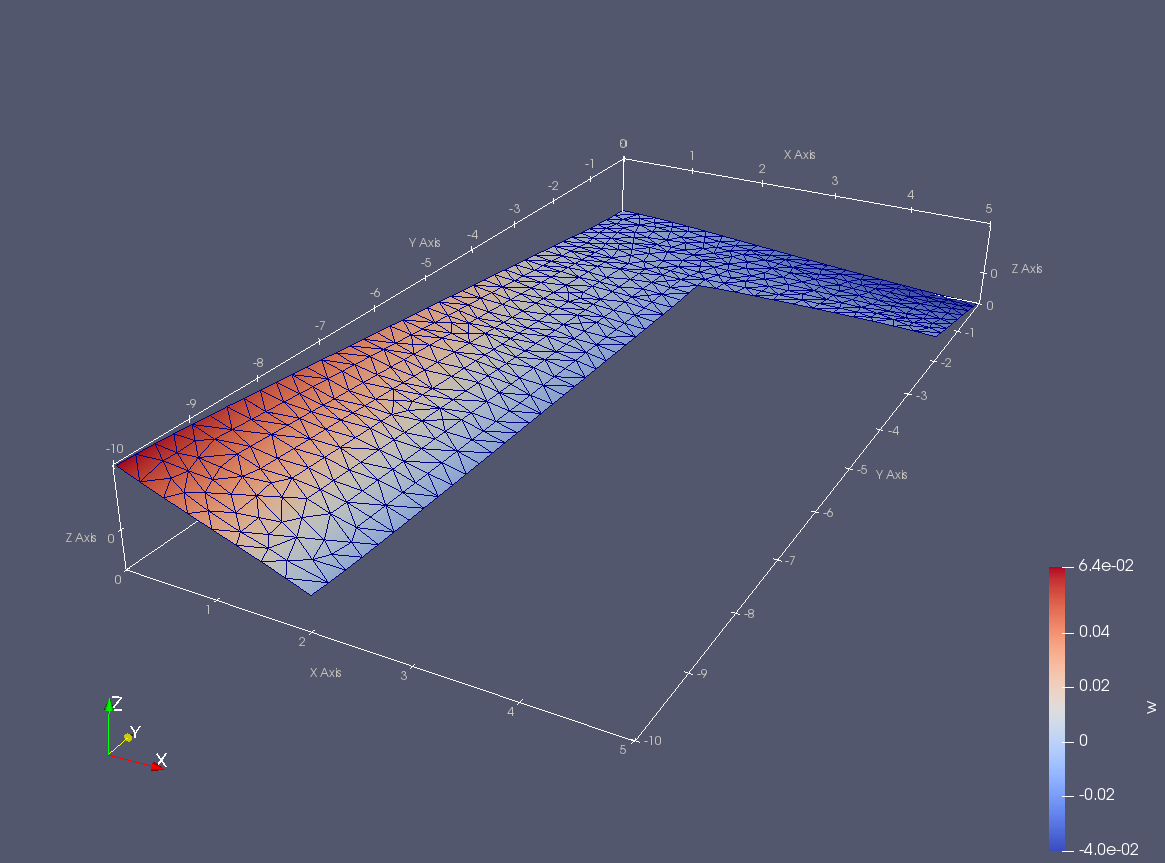
Zkroucený příčný průřez prutu \(u_z=\theta w\).

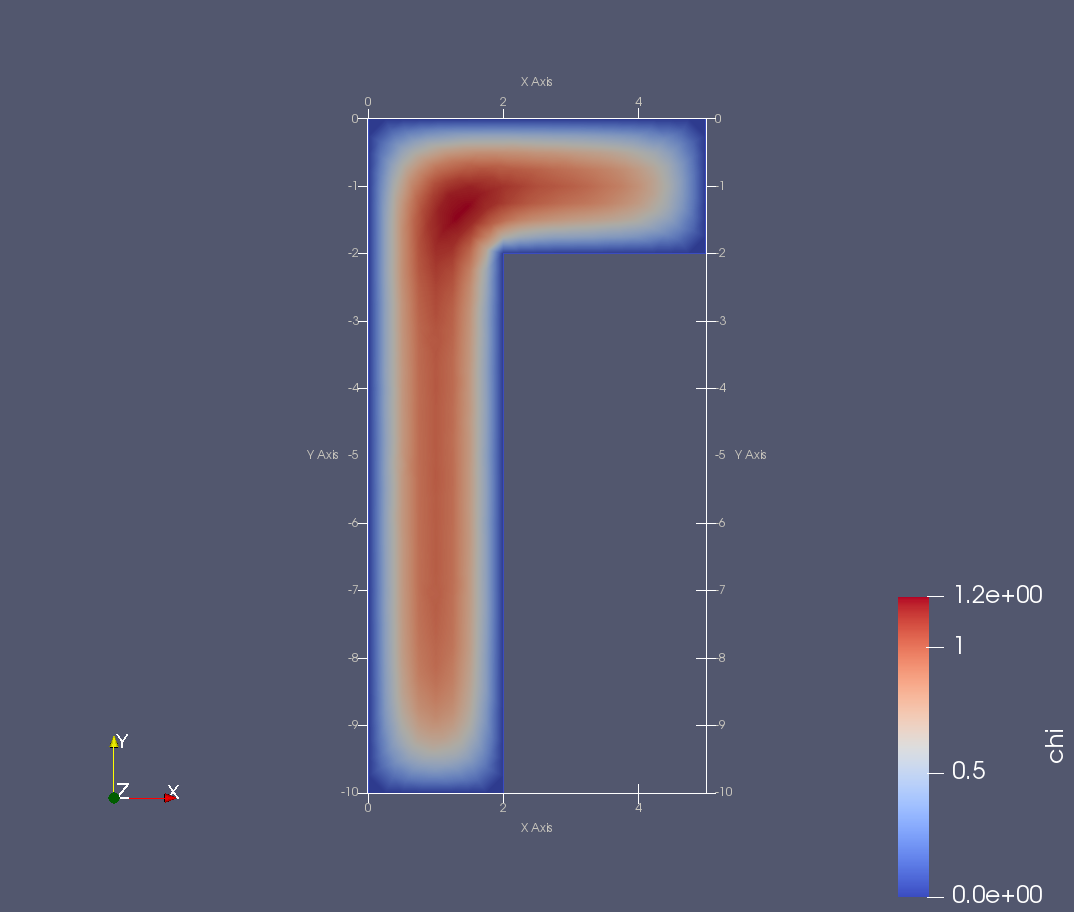
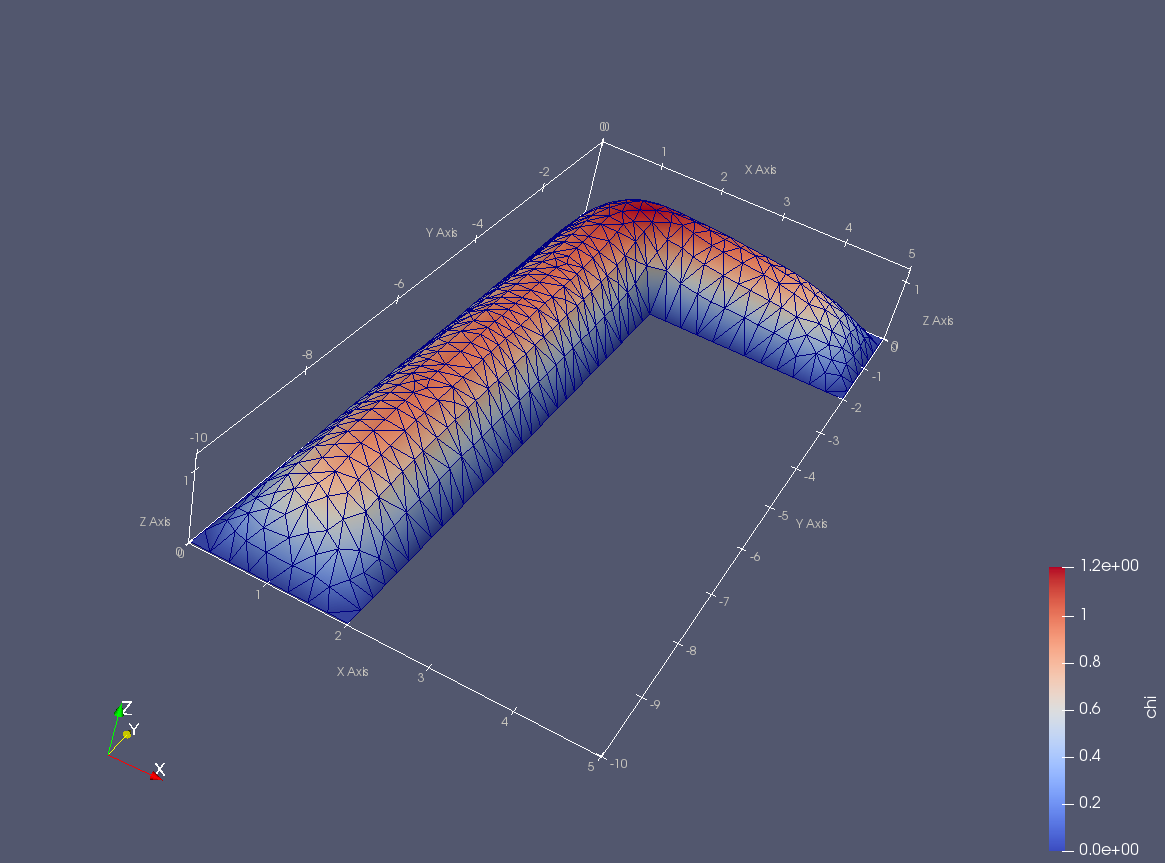
Prandtlova funkce napětí \(\chi\).

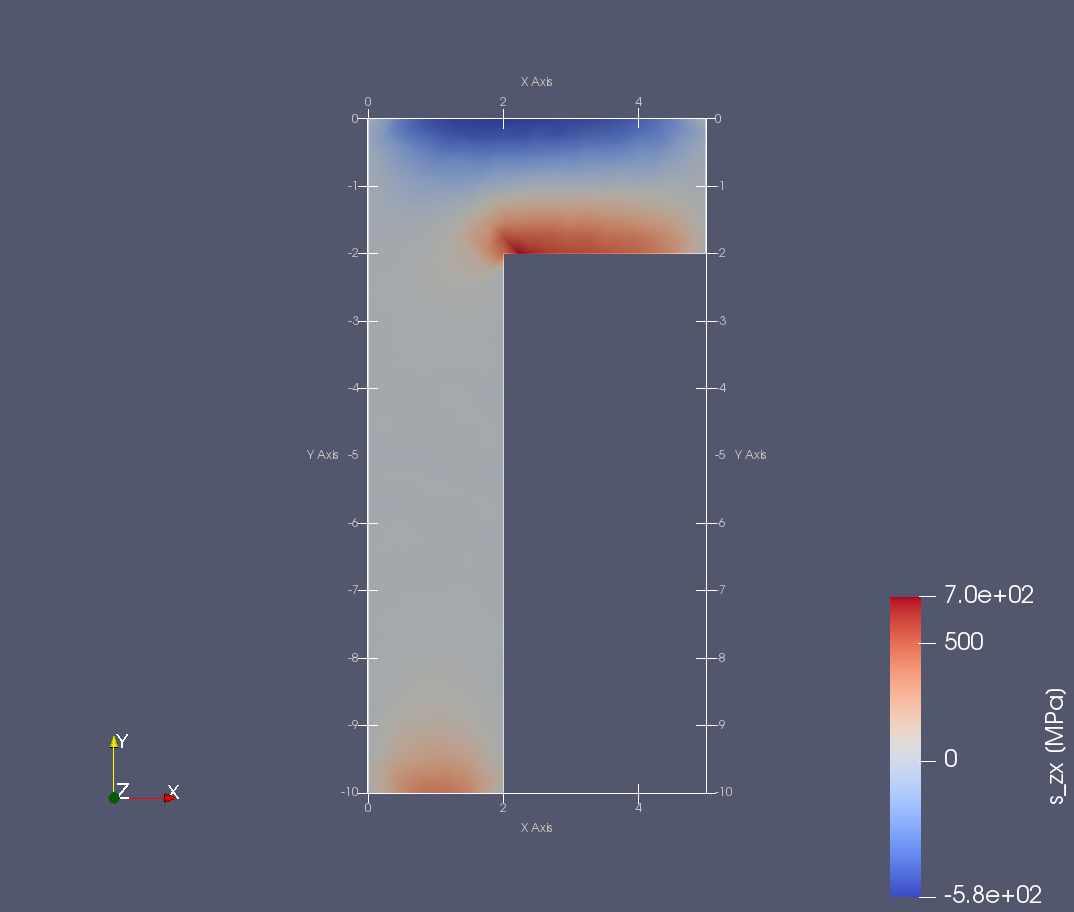
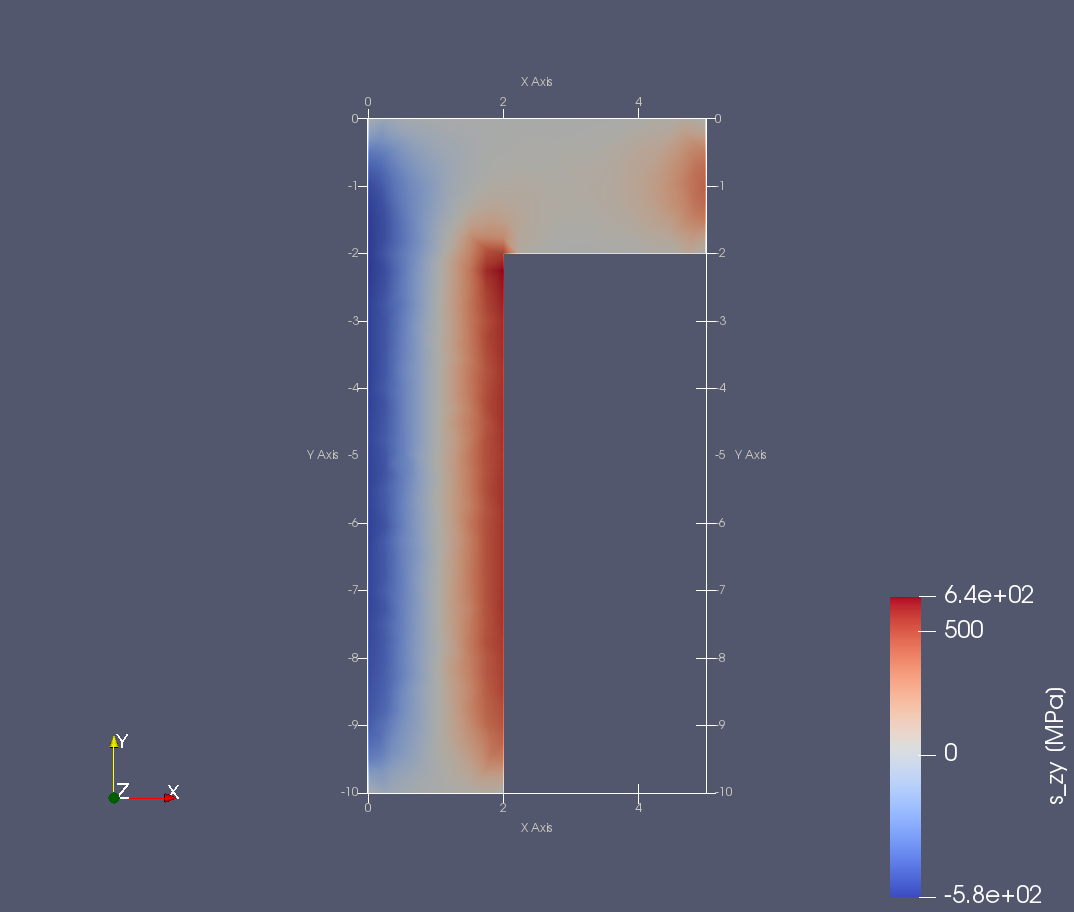
Složky napětí \(\sigma_{zx}\) a \(\sigma_{zy}\).

Průhyb nekruhové membrány se smíšenými okrajovými podmínkami (FreeFEM++ v4.2.1)

Následující úloha je převzata z dokumentace ke konečnoprvkovému systému FreeFEM++, viz. freefem.org. Průhyb \(\varphi\equiv\varphi(x)\) elastické tenké membrány \(\Omega\) s hranicí \(\Gamma\) zatížené silou \(f(x)\mathrm{d}\Omega\) na každém elementu membrány \(\mathrm{d}\Omega\) lze popsat Poissonovou rovnicí

(12)\[-\Delta\varphi=f\quad\mathrm{na}\ \Omega\]

s Dirichletovou, příp. Neumannovou, okrajovou podmínkou

(13)\[\varphi=\varphi_1\quad\mathrm{na}\ \Gamma_1,\quad\partial_n\varphi=\varphi_2\quad\mathrm{na}\ \Gamma_2,\]

kde \(\Gamma=\Gamma_1\cup\Gamma_2\). Výraz \(\partial_n\) se může psát jako

(14)\[\partial_n\equiv\nabla\varphi\cdot\boldsymbol{n},\]

tedy jako skalární součin mezi vnější normálou \(\boldsymbol{n}\) k hranici \(\Gamma\) a gradientem funkce \(\varphi\equiv\varphi(x,y)\) (vektorem reprezentujícím největší spád plochy \(\varphi\equiv\varphi(x,y)\) v bodě \((x,y)\) hranice \(\Gamma\)). Zbývá slabá formulace úlohy

(15)\[\int_\Omega\nabla\varphi\cdot\nabla v\mathrm{d}\Omega=\int_\Omega fv\mathrm{d}\Omega -\int_{\Gamma_2}\varphi_2v\mathrm{d}\Gamma, \qquad\varphi=\varphi_1\quad\mathrm{na}\ \Gamma_1,\]

kde \(v\) je libovolná funkce z jistého prostoru konečných prvků na diskretizované oblasti \(\Omega\).

Formulace problému

Cílem je vyjádřit průhyb membrány \(\Omega\) eliptického tvaru zatížené jednotkovým zatížením \(f(x)=1\). Tvar hranice \(\Gamma\) oblasti \(\Omega\) se může popsat parametricky

(16)\[x=a\cos t,\quad y=b\sin t\quad\mathrm{pro}\ t\in(0,2\pi),\]

kde \(a\) a \(b\) jsou délky hlavní a vedlejší osy elipsy. Podél části hranice \(\Gamma_1\) danou úsekem \(t\in(0,4\pi/3)\) hranice \(\Gamma\) je předepsán průhyb \(\varphi_1=x\) (Dirichletova okrajová podmínka), tj.

(17)\[\varphi=x\quad\mathrm{na}\ \Gamma_1\equiv\big\{(x,y):x=a\cos t,y=b\sin t,t\in(0,4\pi/3)\big\}.\]

Zbývající část hranice \(\Gamma_2=\Gamma-\Gamma_1\) je volná a bez zatížení, nebo-li

(18)\[\partial_n\varphi=0\quad\mathrm{na}\ \Gamma_2=\Gamma-\Gamma_1.\]

Jinými slovy, z důvodu tuhosti membrány se její část u volné hranice vždy natočí do směru vnější normály hranice \(\boldsymbol{n}\).

Řešení

Skript pro FreeFEM++ lze stáhnout zde, jehož výstupy jsou na následujících obrázcích.

Hranice oblasti \(\Omega\) ve tvaru elipsy. Šipky značí orientaci hranice \(\Gamma\), přičemž oblast \(\Omega\) leží na levé straně orientované hranice \(\Gamma\). Barevně jsou odlišeny části hranice \(\Gamma_1\) (delší) a \(\Gamma_2\).

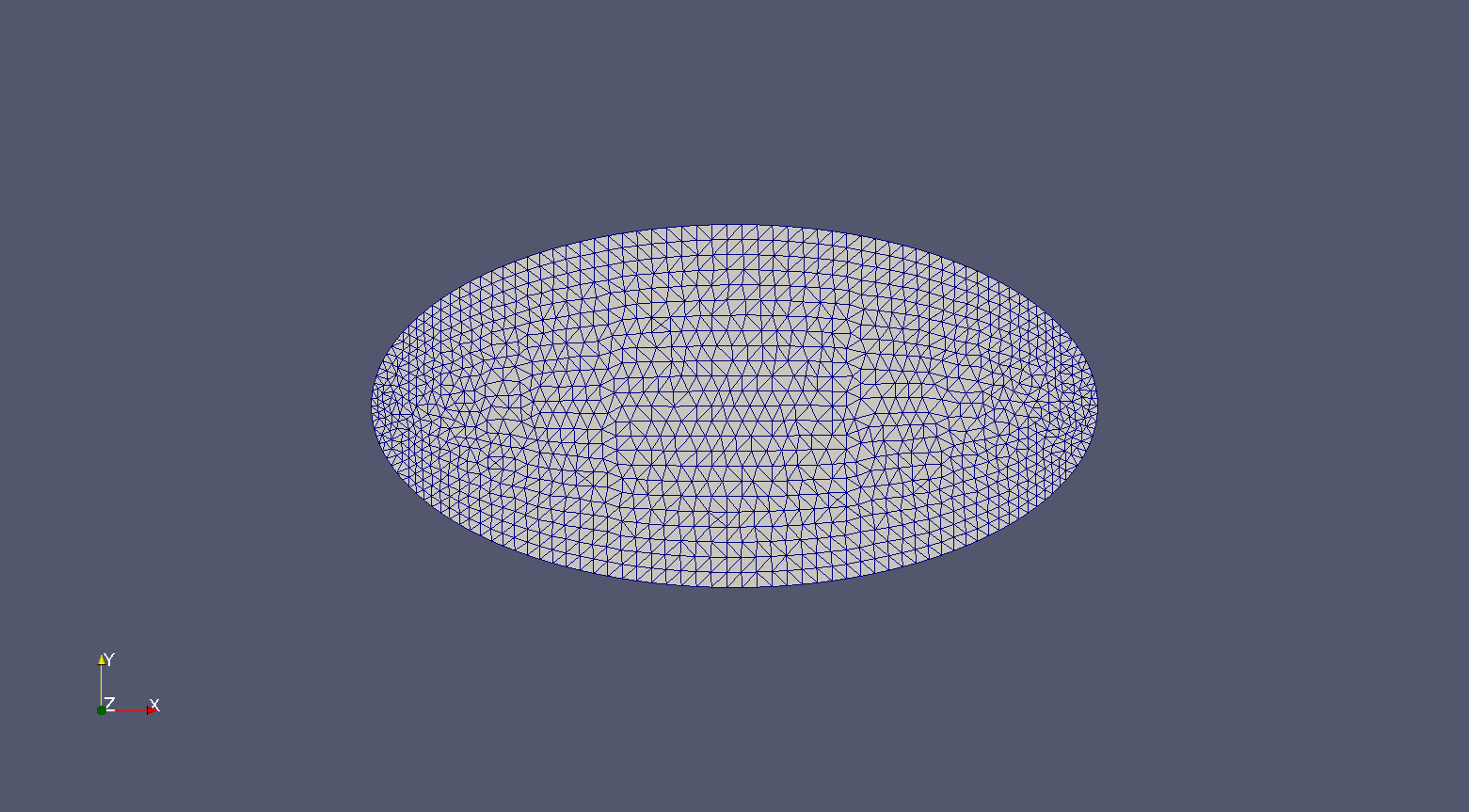
Konečnoprvková síť oblasti \(\Omega\).

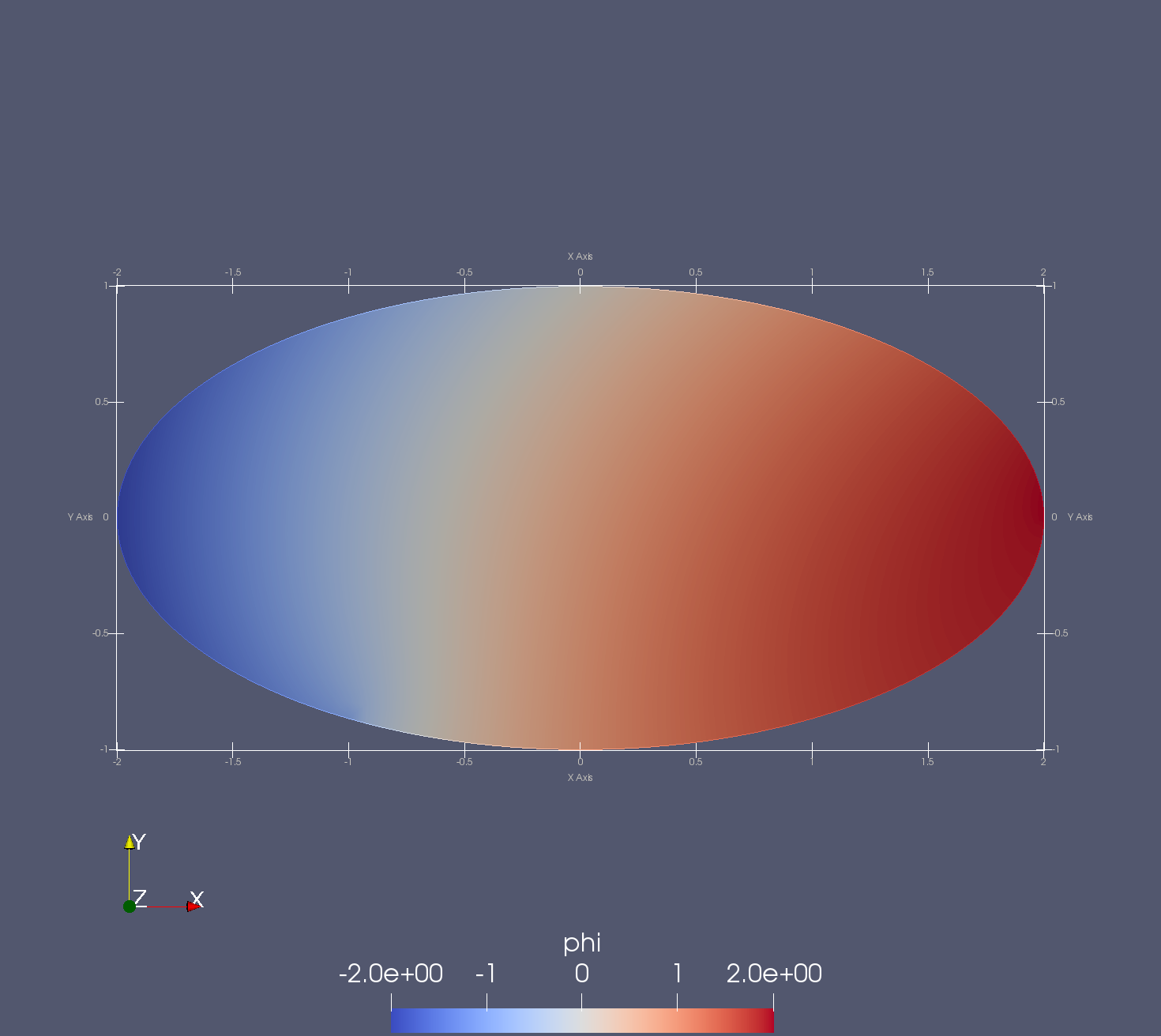
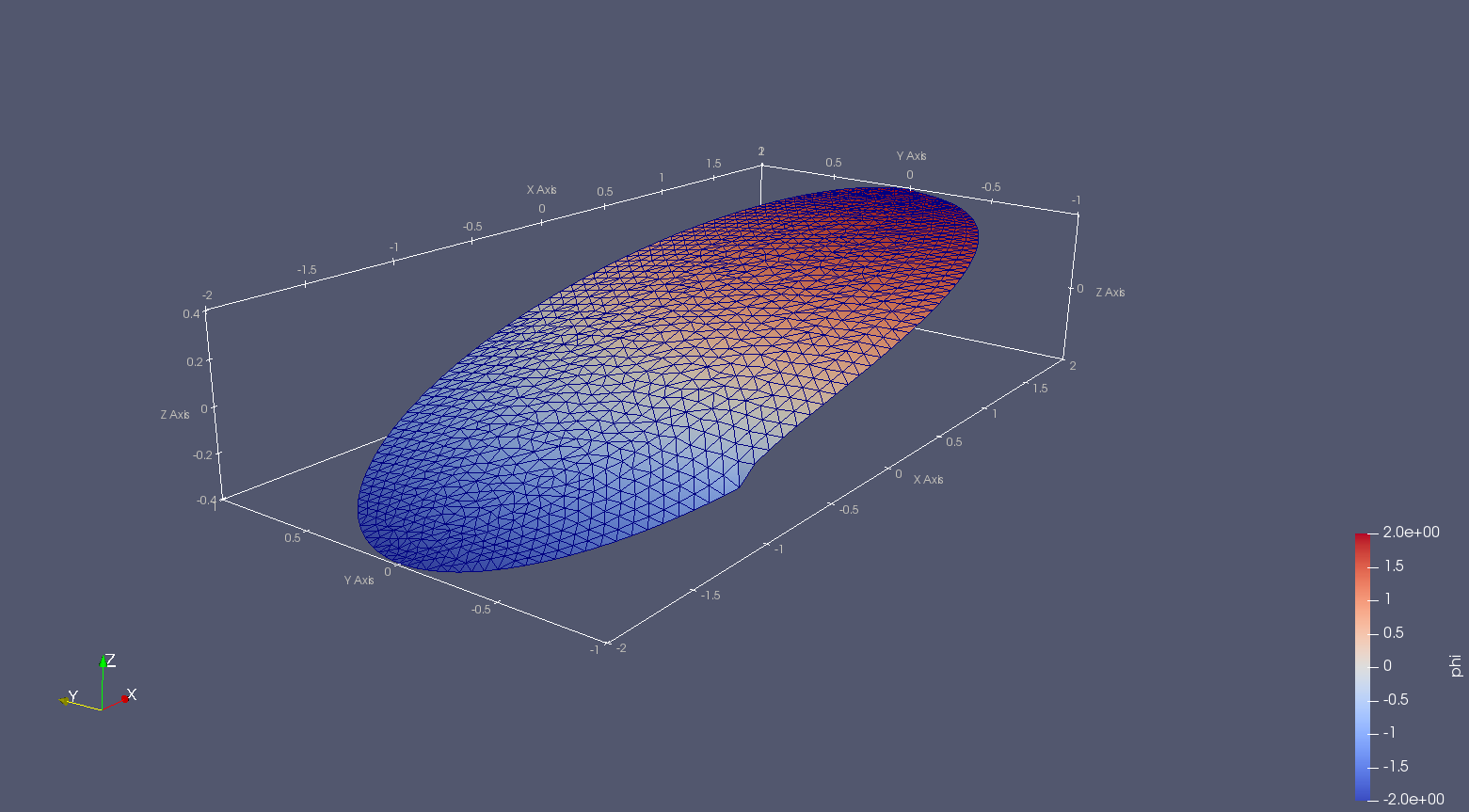
Průhyb membrány \(u_z=\varphi(x,y)\).

Průhyb bi-materilového teplotně zatíženého prutu (FreeFEM++ v4.2.1)

V rovinné izotropní pružnosti (konkrétně v případě rovinné deformace) kontinuum podléhá zákonům, jež zachycuje následující soustava parciálních diferenciální rovnic a konstitutivních vztahů

(19)\[\nabla\cdot\boldsymbol{\sigma}=0,\]

(20)\[\boldsymbol{\sigma}=\lambda\big(\nabla\cdot\boldsymbol{u}\big)\boldsymbol{I} +\mu\big(\boldsymbol{u}\nabla+\nabla\boldsymbol{u}\big) -\big(3\lambda+2\mu\big)\alpha_T\Delta T\boldsymbol{I},\]

kde \(\boldsymbol{u}\) a \(\boldsymbol{\sigma}\) jsou vektor posuvů a tenzor napětí a \(\boldsymbol{I}\) je jednotkový tenzor. V posledních (konstitutivních) vztazích je zavedeno běžné označení \(\lambda\) a \(\mu\) pro Lamého konstanty a označení \(\alpha_T\) a \(\Delta T\) pro teplotní roztažnost materiálu a změnu teploty. Okrajové podmínky jsou Dirichletova a Neumannova na části hranice \(\Gamma_1\) a \(\Gamma_2\),

(21)\[\boldsymbol{u}=\boldsymbol{u}_1\quad\mathrm{na}\ \Gamma_1, \qquad\boldsymbol{t}=\boldsymbol{\sigma}_2\cdot\boldsymbol{n}_2\quad\mathrm{na}\ \Gamma_2,\]

kde \(\Gamma=\Gamma_1\cup\Gamma_2\) a \(\boldsymbol{n}_2\) je vnější normála k hranici \(\Gamma_2\). Slabá formulace úlohy se může zapsat následovně

(22)\[\begin{split}\begin{equation} \begin{split} & \int_\Omega\lambda\big(\nabla\cdot\boldsymbol{u}\big)\big(\nabla\cdot\boldsymbol{v}\big)\mathrm{d}\Omega +\int_\Omega\frac{\mu}{2}\big(\boldsymbol{u}\nabla+\nabla\boldsymbol{u}\big) \cdot\big(\boldsymbol{v}\nabla+\nabla\boldsymbol{v}\big)\mathrm{d}\Omega \\ & -\int_\Omega(3\lambda+2\mu)\alpha_T\Delta T\big(\nabla\cdot\boldsymbol{v}\big)\boldsymbol{d}\Omega= \int_{\Gamma_2}\big(\boldsymbol{\sigma}_2\cdot\boldsymbol{n}_2\big)\cdot\boldsymbol{v}\mathrm{d}\Gamma, \end{split} \end{equation}\end{split}\]

(23)\[\boldsymbol{u}=\boldsymbol{u}_1\quad\mathrm{na}\ \Gamma_1,\]

kde \(\boldsymbol{v}\) je libovolný vektor z jistého prostoru funkcí definovaného nad diskretizovaným prostorem \(\Omega\).

Formulace problému

Cílem je vyjádřit průhyb bi-materiálového prutu \(\Omega\) o délce \(l=10\ \mathrm{mm}\) a šířce \(h=2\ \mathrm{mm}\), jak ukazuje následující obrázek.

Rozměry prutu s bi-materiálovým rozhraním podél podélné osy (střednice) prutu.

Charakteristiky dolního a horního materiálu \(I\) a \(II\) ukazuje následující tabulka.

materiál	\(I\)	\(II\)
\(E\)	\(2.10\times 10^{5}\,\mathrm{MPa}\)	\(1.10\times 10^{5}\,\mathrm{MPa}\)
\(\nu\)	\(0.28\)	\(0.30\)
\(\alpha_T\)	\(1.00\times 10^{-5}\,\mathrm{K}^{-1}\)	\(1.00\times 10^{-4}\,\mathrm{K}^{-1}\)

Prut není zatížen mechanicky, pouze teplotně změnou teploty \(\Delta T=1\ \mathrm{K}.i\), přičemž levý konec prutu je vetknut, z čehož plynou následující okrajové podmínky

(24)\[\begin{split}\begin{equation} \begin{split} \boldsymbol{u}\equiv\big(u_x,u_y\big)=(0,0) \quad\mathrm{pro} &\ x=0\wedge y\in(0,2)\ \mathrm{mm}, \\ \boldsymbol{t}\equiv\big(t_x,t_y\big)=(0,0) \quad\mathrm{pro} &\ x\in(0,10)\ \mathrm{mm} \wedge y=0\,\mathrm{mm}, \\ &\ x=10\,\mathrm{mm} \wedge y\in(0,2)\,\mathrm{mm}, \\ &\ \mathrm{a}\ x\in(0,10)\,\mathrm{mm} \wedge y=2\,\mathrm{mm}. \end{split} \end{equation}\end{split}\]

Řešení

Skript pro FreeFEM++ lze stáhnout zde, jehož výstupy jsou na následujících obrázcích.

Hranice prutu \(\Omega\). Šipky značí orientaci hranice \(\Gamma\), přičemž oblast \(\Omega\) leží na levé straně orientované hranice \(\Gamma\). Barevně jsou odlišeny různé části hranice. Na obrázku je také uvedena vnitřní hranice \(x=5\,\mathrm{mm}\), podél které se vykreslují křivky posuvů a napětí, viz. níže.

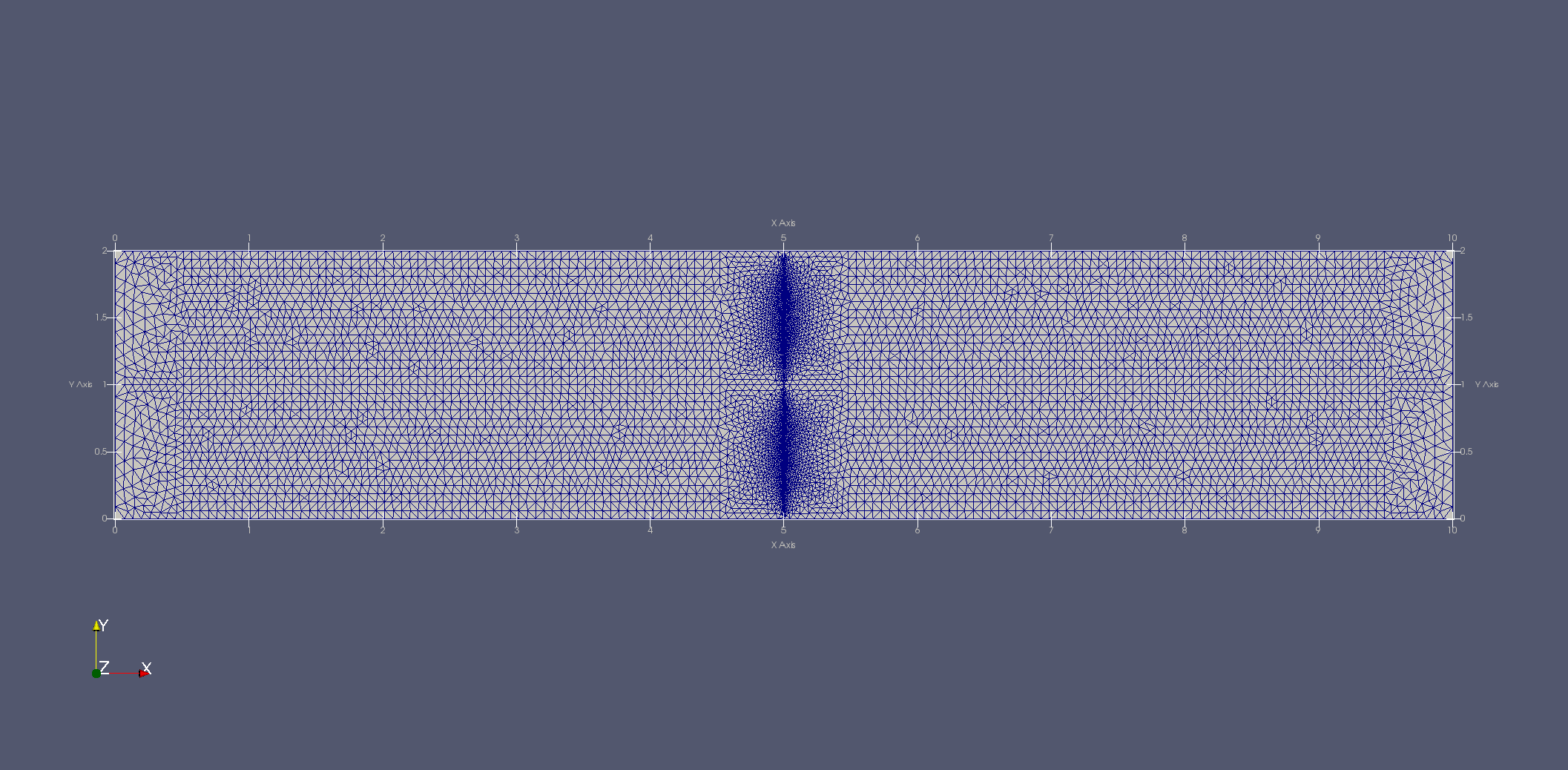
Konečnoprvková síť oblasti \(\Omega\) definující bi-materiálový prut. Zjemnění sítě podél úsečky \(x=5\,\mathrm{mm}\) je z důvodu vykreslení dostatečně hladkých křivek posuvů a napětí v příčném průřezu, viz. níže.

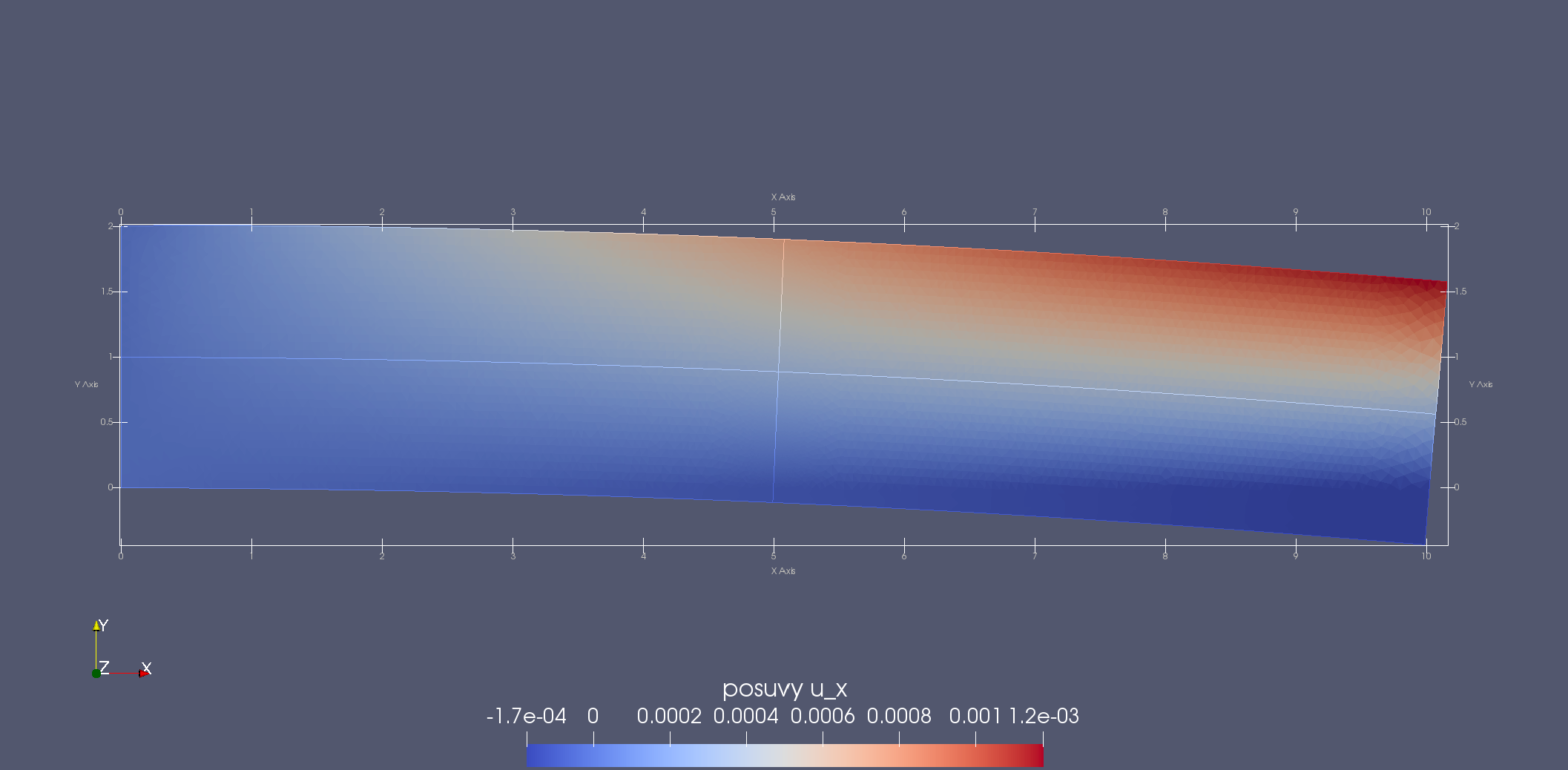
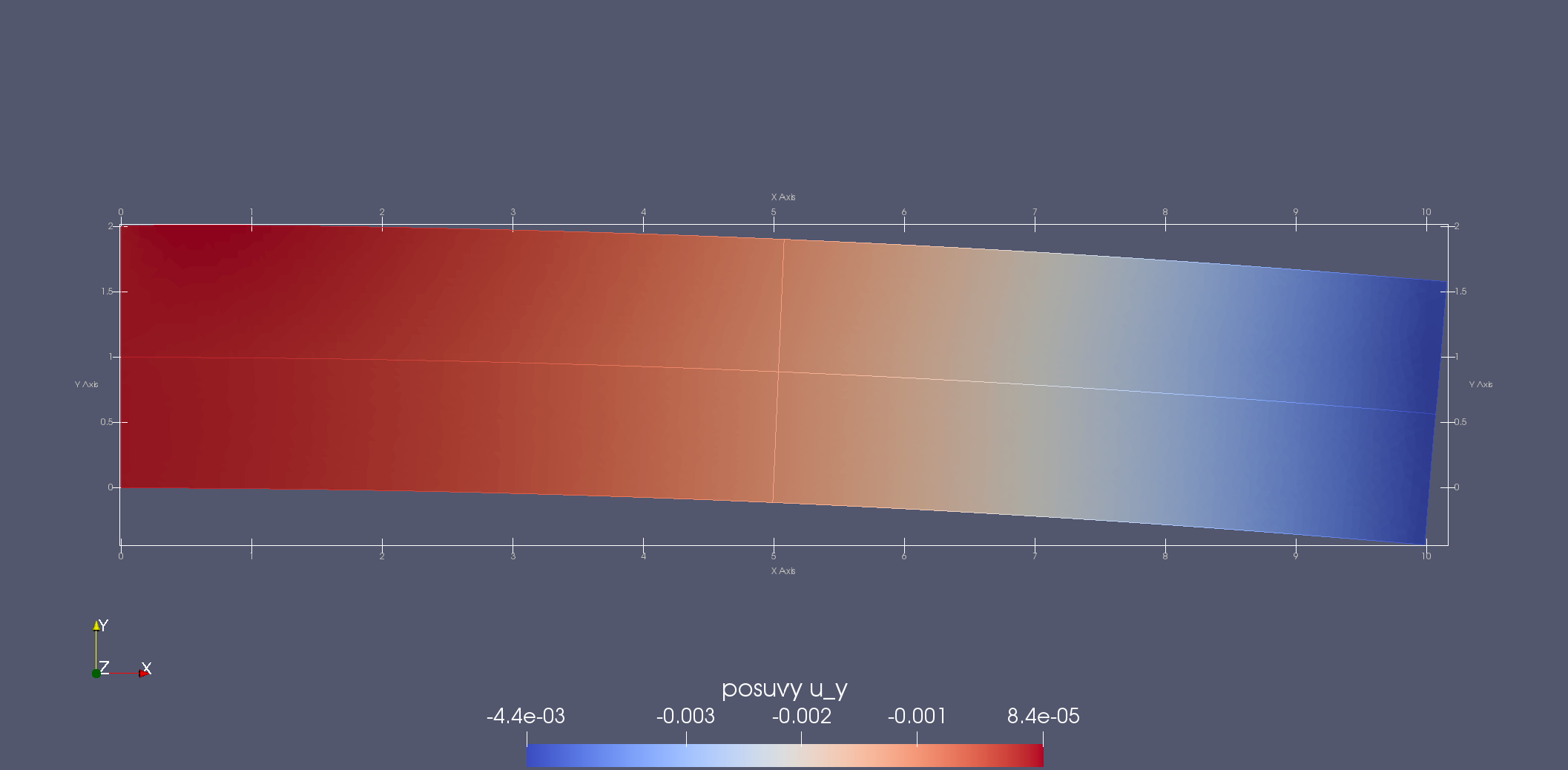
Prodloužení \(u_x\) a průhyb \(u_y\) prutu.

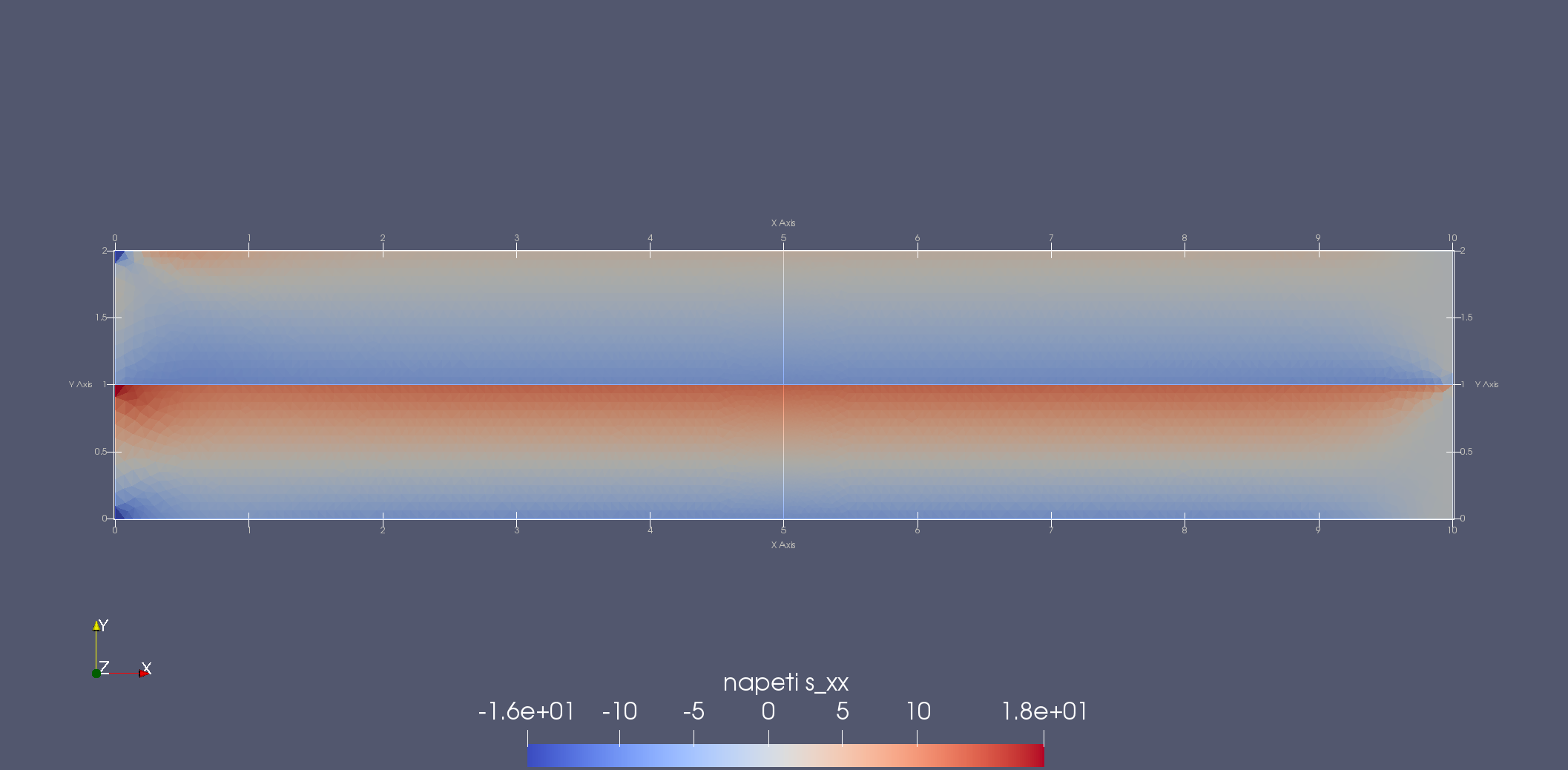
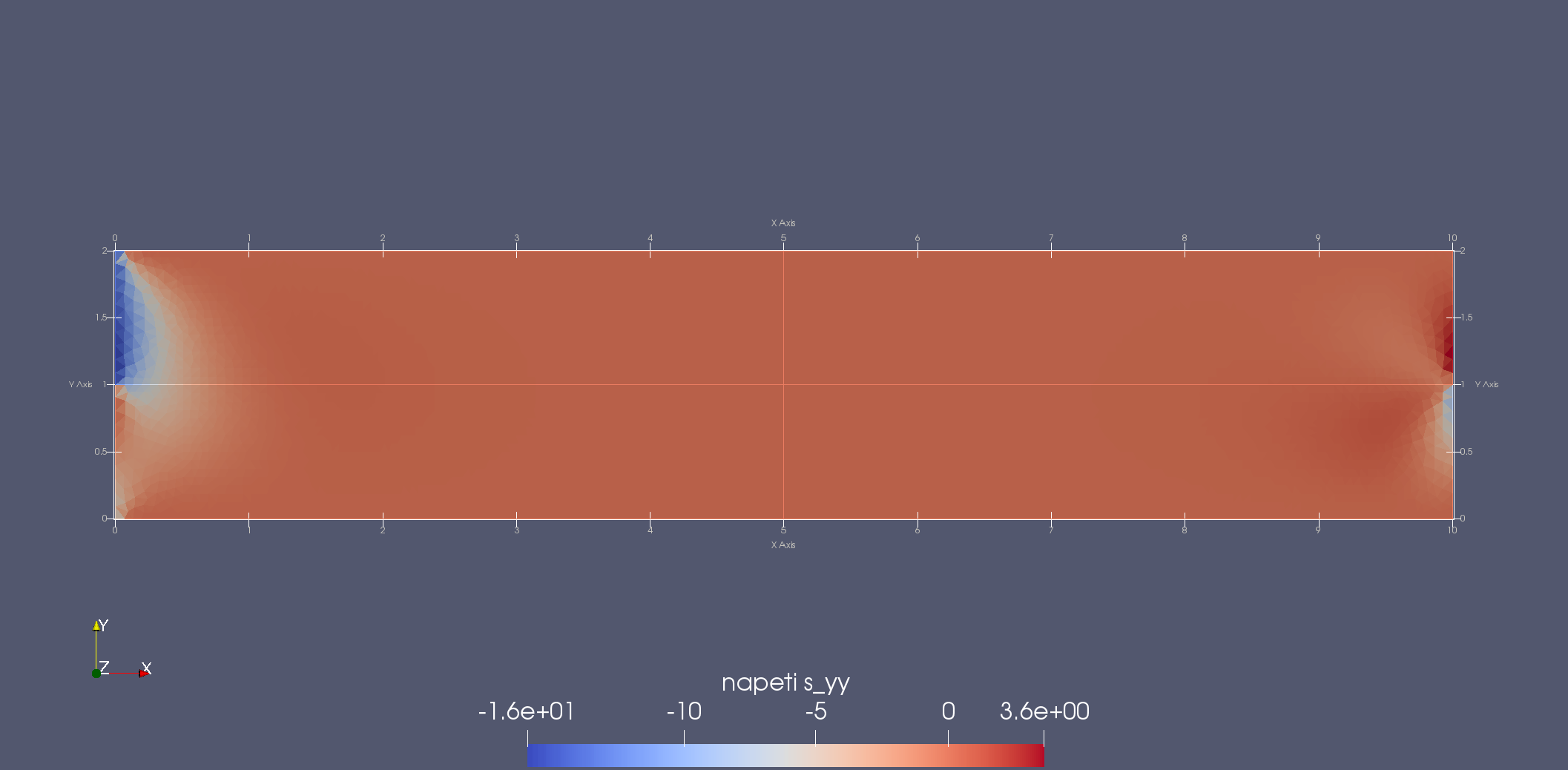
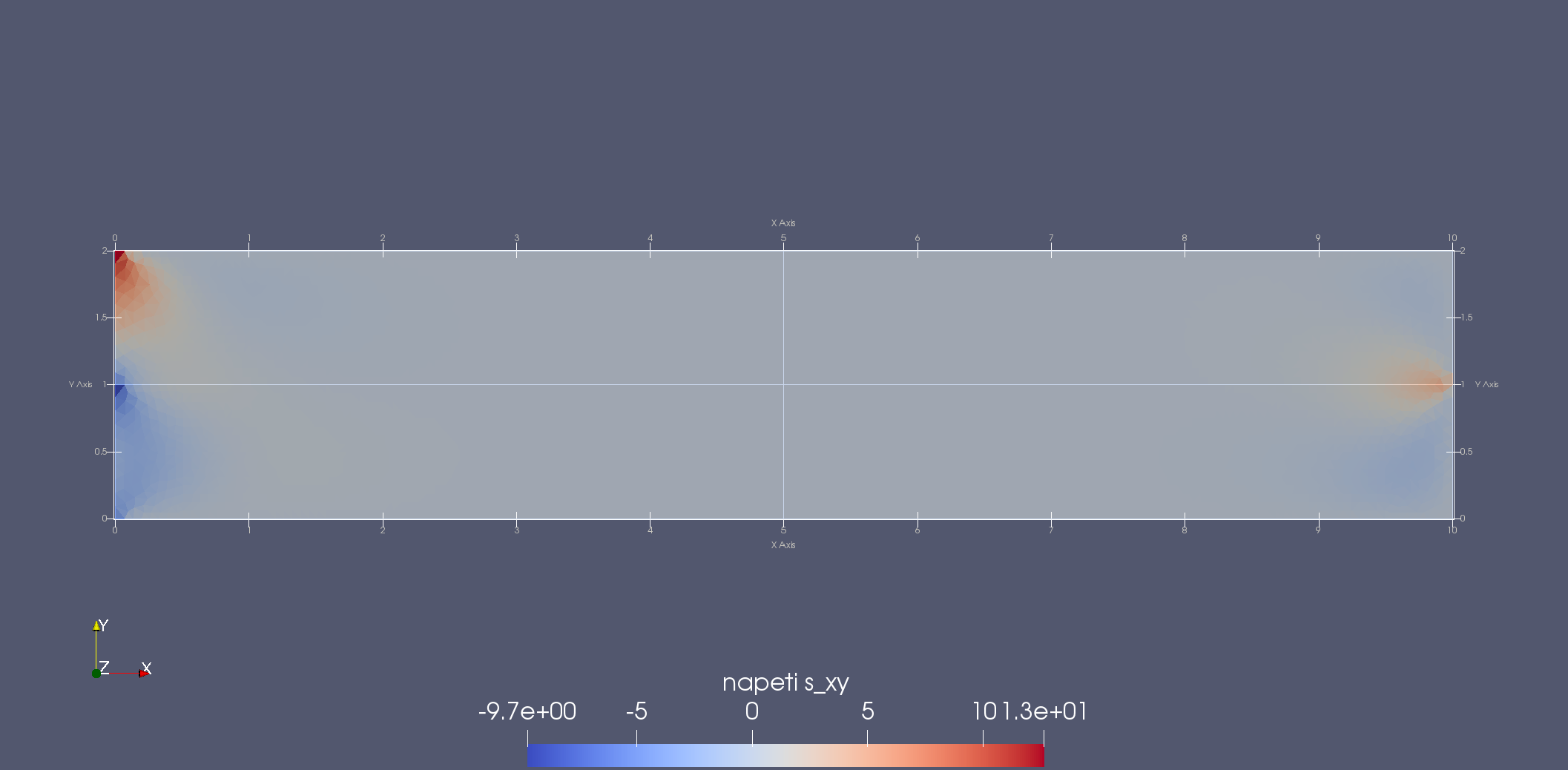
Složky tenzoru napětí \(\sigma_{xx}\), \(\sigma_{yy}\) a \(\sigma_{xy}\). Dobře jde vidět nespojitost napětí \(\sigma_{xx}\) podél bi-materiálového rozhraní a zanedbatelně malé hodnoty napětí \(\sigma_{yy}\) a \(\sigma_{xy}\). Zajímavá je koncentrace napětí v místech, kde nejsou splněny prutové předpoklady, tj. ve vetknutí a na volném konci, kde se rozhraní chová jako vrub.

Následující grafy vykreslují průběh posuvů a napětí v příčném průřezu \(x=5\,\mathrm{mm}\). Potřebný skript pro vykreslení grafů v Pythonu lze stáhnout zde.

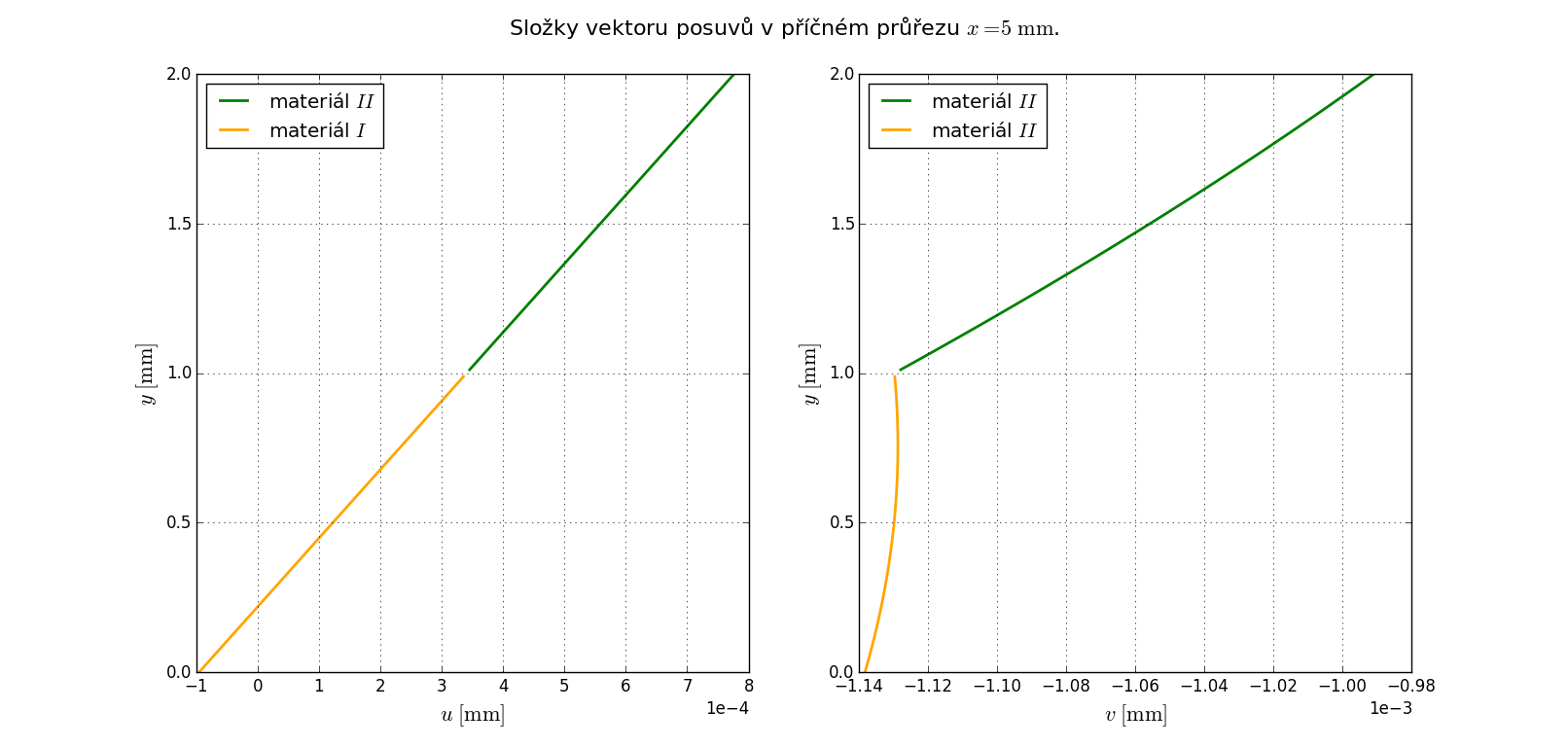
Složky \(u_x\) a \(u_y\) vektoru posuvu \(\boldsymbol{u}\) v příčném průřezu \(x=5\,\mathrm{mm}\).

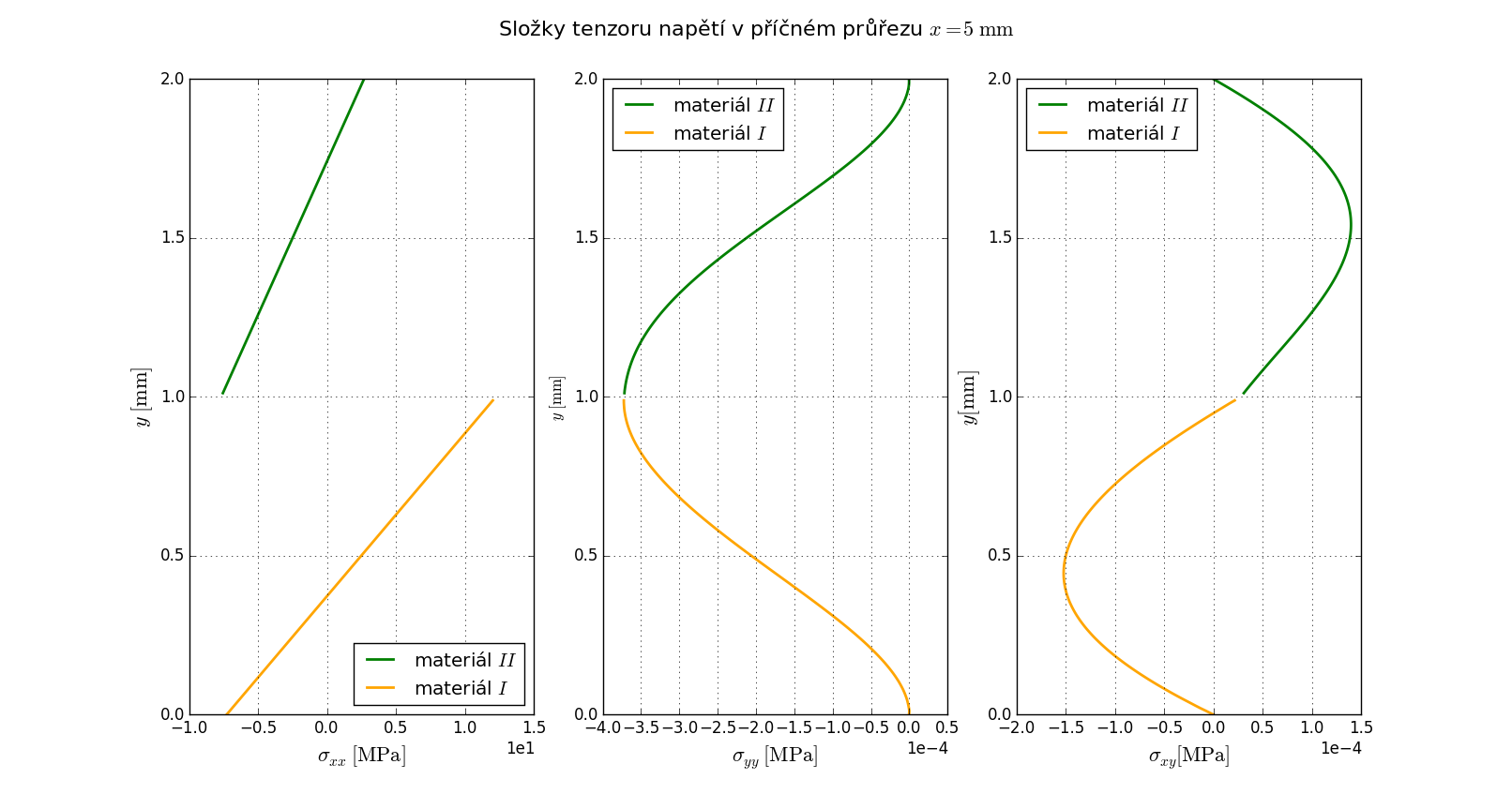
Složky \(\sigma_{xx}\), \(\sigma_{yy}\) a \(\sigma_{xy}\) tenzoru napětí \(\boldsymbol{\sigma}\) v příčném průřezu \(x=5\,\mathrm{mm}\). Jde viděl lineární průběh napětí \(\sigma_{xx}\) a jeho nespojitost na rozhraní bi-materiálu. Dále jdou vidět téměř nulové hodnoty napětí \(\sigma_{yy}\) a \(\sigma_{xy}\), jejich nulové hodnoty na vnějším povrchu \(y=0\,\mathrm{mm}\) a \(y=2\,\mathrm{mm}\) a spojitost na rozhraní bi-materiálu.

Metoda konečných prvků - FEniCS

FEniCS je volně dostupný konečnoprvkový software, podobně jako projekt FreeFEM++. Je specifický způsobem formulování řešené úlohy pomocí jazyka UFL (Unified Form Language), který může být kompilován pomocí C++ nebo interpretovaný pomocí Pythonu. Potřebné informace o projektu FEniCS lze nalézt na stránkách projektu fenicsproject.org. Níže je ukázka použití FEniCSu pro řešení Poissonovy rovnice. FEniCS v2017.2.0 byl vybaven skromnými nástroji pro tvorbu konečnoprvkové sítě. Vyšší verze FEniCS v2019 již těmito nástroji nedisponuje, dokáže však zpracovat konečnoprvkové sítě vytvořené externími programy. S nastupující verzí FEniCS X autor zatím nemá zkušenosti. V případě níže zpracované úlohy byl k tomuto účelu použit volně dostupný program gmsh.info.

Poissonova rovnice s podoblastmi (FEniCS 2017.2.0)

Následující příklad demonstruje formulaci a řešení variačního problému Poissonovy rovnice definované na dvou různých oblastech s různými okrajovými podmínkami.

Formulace problému

Uvažujme Poissonovu rovnici definovanou na jednotkovém čtverci \(\Omega=[0,1]\times [0,1]\) s různými typem okrajových podmínek. Nechť tedy \(u\) vyhovuje následující diferenciální rovnici

(25)\[\begin{split}\begin{equation} \begin{split} -\mathrm{div}\left(a\nabla u\right) &= 1.0\quad\mathrm{na}\ \Omega, \\ u &= 5.0\quad\mathrm{na}\ \Gamma_T, \\ u &= 0.0\quad\mathrm{na}\ \Gamma_B, \\ \nabla u\cdot n &= -10.0\mathrm{e}^{-(y-0.5)^2}\quad\mathrm{na}\ \Gamma_L, \\ \nabla u\cdot n &= 1.0\quad\mathrm{na}\ \Gamma_R, \end{split} \end{equation}\end{split}\]

kde \(\Gamma_T\), \(\Gamma_B\), \(\Gamma_L\) a \(\Gamma_R\) značí horní, spodní, levou a pravou hranu oblasti \(\Omega\). Hodnoty koeficientu \(a\) se mohou měnit v závislosti na poloze v oblasti \(\Omega\) a zvolíme ho následovně

(26)\[\begin{split}\begin{equation} \begin{split} a &= a_1 = 0.01\quad\mathrm{pro}\ (x,y)\in\Omega_1=[0.2,1.0]\times[0.5,0.7], \\ a &= a_0 = 1\quad\mathrm{pro}\ (x,y)\in\Omega_0=\Omega\setminus\Omega_1. \end{split} \end{equation}\end{split}\]

Podoblast \(\Omega_1\) může být chápaná jako inkluze s jinými materiálovými vlastnostmi.

Variační forma

Výše popsaná okrajová úloha se může zapsat ve variační formě. Jestliže \(u\in V\) tak, že

(27)\[a(u,v)=L(v)\quad\forall v\in\hat{V},\]

kde \(V\) a \(\hat{V}\) jsou vhodné prostory funkcí vyhovující Dirichletovým okrajovým podmínkám na \(\Gamma_T\) a \(\Gamma_B\) a

(28)\[\begin{split}\begin{equation} \begin{split} a(u,v) &= \int_{\Omega_0}a_0\nabla u\cdot\nabla v\mathrm{d}x+\int_{\Omega_1}a_1\nabla u\cdot\nabla v\mathrm{d}x, \\ L(v) &= \int_{\Gamma_L}g_Lv\mathrm{d}s+\int_{\Gamma_R}g_Rv\mathrm{d}s+\int_{\Omega}fv\mathrm{d}x, \end{split} \end{equation}\end{split}\]

kde \(f=1.0\), \(g_L=-10.0\mathrm{e}^{-(y-0.5)^2}\) a \(g_R=1.0\).

Implementace bez GMSH

Výše formulovaný příklad kombinuje různé okrajové podmínky a různé materiálové vlastnosti různých částí oblasti, na které se řešení hledá. Tyto informace je samozřejmě nutné FEniCSu předat. To se provede tak, že se podoblastem přiřadí indexy a později se přes tyto oblasti provede integrace. Knihovna DOLFIN, která je součástí FEniCSu, nabízí třídu MeshFunction jejíž instance reprezentuje funkci definovanou nad diskretizovanou oblastí (např. nad prvky nebo jejich hranicemi). Tyto funkce mohou být načteny ze souboru nebo mohou být definovány pomocí instancí další třídy SubDomain, jestliže jsou podoblasti explicitně definovány. To je také případ výše formulované úlohy. Nejdříve se pomocí třídy SubDomain vytvoří instance definující levou, pravou, horní a dolní část hranice oblasti a pak vnitřní podoblasti.

from dolfin import *
import matplotlib.pyplot as plt

#-----[vytvoreni trid pro podoblasti a casti hranic]-----

class Left(SubDomain):
  def inside(self,x,on_boundary):
    return near(x[0],0.0)

class Right(SubDomain):
  def inside(self,x,on_boundary):
    return near(x[0],1.0)

class Bottom(SubDomain):
  def inside(self,x,on_boundary):
    return near(x[1],0.0)

class Top(SubDomain):
  def inside(self,x,on_boundary):
    return near(x[1],1.0)

class Obstacle(SubDomain):
  def inside(self,x,on_boundary):
    return (between(x[1],(0.5,0.7)) and between(x[0],(0.2,1.0)))

#-----[instance trid podoblasti]-----

left=Left()
top=Top()
right=Right()
bottom=Bottom()
obstacle=Obstacle()

Zde je vhodné upozornit na funkce near a between, které nabízí způsob zjištění, zda se souřadnice x nacházejí v blízkosti dané hodnoty nebo mezi danými hodnotami v rámci strojové numerické přesnosti.

Další poznámka souvisí se způsobem komunikace s DOLFINem. Každá uživatelem vytvořená třída Right, Left atd. dědí vlastnosti a metody DOLFINovy třídy SubDomain. Takovou metodou je i např. funkce inside, která vrací pravdivou nebo nepravdivou hodnotu, podle toho zda se souřadnice x nachází v dané části oblasti, či nikoli. Tím, že se do nové třídy napíše, přepíše se její původní tvar z SubDomain, ale FEniCS přes knihovnu DOLFIN s ní bude stále stejně zacházet. Prostě a jednoduše, komunikace s DOLFINem probíhá tak, že uživatel přepisuje DOLFINem definované metody tříd k obrazu svému.

V dalším kroku se oblast ve tvaru jednotkového čtverce diskretizovanou trojúhelníkovými prvky po 64 na každé straně.

#-----[vymeshovani jednotkoveho ctverce]-----

mesh=UnitSquareMesh(64,64)

K manipulaci s konečnoprvkovou sítí oblastí v DOLFINu slouží funkce MeshFunction. Umožňuje např. vybrat prvky diskretizované oblasti, přiřadit jim indexy nebo celé, reálné i logické hodnoty. Takto se mohou rozdělit prvky, které by měli patřit do oblasti \(\Omega_0\) a do oblasti \(\Omega_1\). V úloze se prvkům přiřadí indexy podle indexů oblastí, do které patří. To zajistí parametr size_t. Další parametr funkce MeshFunction je zřejmý a poslední, tj. mesh.topology().dim() říká, že jde o část vnitřku oblasti \(\Omega\). Nejdříve se všem prvkům pomocí metody set_all přiřadí index \(0\) a pak se prvkům z oblasti \(\Omega_1\) reprezentované objektem obstacle přiřadí pomocí metody mark index \(1\).

#-----[inicializovani vnitrku prvku vymeshovane oblasti]-----

domains=MeshFunction("size_t",mesh,mesh.topology().dim())

#-----[prirazeni nuloveho indexu vnitrkum vsech prvku]-----

domains.set_all(0)

#-----[prirazeni indexu 1 vymezene podoblasti >obstacle<]-----

obstacle.mark(domains,1)

Podobně se indexy označí hranice oblasti \(\Gamma_L\), \(\Gamma_R\), \(\Gamma_T\) a \(\Gamma_B\). Ve funkci MeshFunction se ale musí snížit dimenze na mesh.topology().dim()-1.

#-----[inicializovani hran prvku vymeshovane oblasti]-----

boundaries=MeshFunction("size_t",mesh,mesh.topology().dim()-1)

#-----[prirazeni nuloveho indexu hranam vsech prvku]-----

boundaries.set_all(0)

#-----[prirazeni hranam prvku tvorici hranici oblasti indexy 1,2,3 a 4]-----

left.mark(boundaries,1)
top.mark(boundaries,2)
right.mark(boundaries,3)
bottom.mark(boundaries,4)

Dříve, než se ve FEniCSu definuje variační úloha (28), zavedou se konstanty a vztahy vystupující ve formulaci úlohy (25) a (26). K tomuto účelu je DOLFIN vybaven třídou Expression, jejíž speciální tvar je třída Constant. Význam a vlastnosti třídy Constant je zřejmý, přičemž její instance nemusí být pouze konstantou, ale také konstantním vektorem. Jednou z metod třídy Expresion je metoda eval, která se opět může předefinovat a vracet hodnotu value podle požadavků dané úlohy. Takto upravená třída a její instance se aproximuje ve vybraném prostoru funkcí, nad kterým se řeší celá úloha. V případě výše formulované úlohy (25) a (26) se jako konečný prostor funkcí volí s bází Lagrangeových polynomů druhého řádu jako instance třídy FunctionSpace. Parametry \(a_0\) a \(a_1\) jsou definovány jako instance třídy Constant. Výrazy Neumannových podmínek na hranici \(\Gamma_L\) a \(\Gamma_R\) jsou instancemi tříd Expression stejně jako pravá strana Poissonovy rovnice \(f\). Nakonec jsou tyto výrazy aproximovány na konečném prostoru Lagrangeových funkcí pomocí metody ufl_element.

#-----[vyber baze prostoru funkci definovaneho nad prvky]-----

V=FunctionSpace(mesh,"CG",2)

#-----[Definice vstupnich hodnot, prip. vyrazu]----

a0=Constant(1.0)
a1=Constant(0.01)

class MyExpression1(Expression):
  def eval(self,value,x):
    value[0]=-10*exp(-(x[1]-0.5)**2)

class MyExpression2(Expression):
  def eval(self,value,x):
    value[0]=1

#-----[instance vyrazu 1 a 2 na bazi prostoru funkci V]-----

g_L=MyExpression1(element=V.ufl_element())
g_R=MyExpression2(element=V.ufl_element())
f=MyExpression2(element=V.ufl_element())

Konečně je možné definovat variační problém (28). Obvykle se začíná definicí konečnoprvkového prostoru funkcí. Tento krok již však byl výše proveden při definici výrazů Expression instancí třídy FunctionSpace. Nyní se na zvoleném konečnoprvkovém prostoru definuje funkce samotného řešení \(u\) a testovací funkce \(v\).

#-----[definovani trial a testovaci funkce]-----

u=TrialFunction(V)
v=TestFunction(V)

Dalším krokem je definice Dirichletových okrajových podmínek, které jsou předepsány na horní a spodní hranici oblasti, tj. na hranicích s indexy 2 a 4.

#-----[definice Dirichletovych okrajovych podminek]-----
#-----[             podel hranice 2 a 4           ]-----

bcs=[DirichletBC(V,5.0,boundaries,2),
     DirichletBC(V,0.0,boundaries,4)]

DOLFIN definuje "míry" dx, ds a dS, které v 2D značí integraci přes plochu prvků, přes "vnější" hrany prvků tvořících vnější hranici oblasti a "vnitřní" hrany všech prvků. Tyto míry mohou být indexované, přesněji "difóltně" mají nastavený index 0, tj. dx je také dx(0), ds je ds(0) a dS je dS(0). Tyto indexy jde měnit např. v závislosti na indexu podoblasti přes kterou se daná integrace provádí. Nejjednodušší způsob, jak to provést, je následující.

#-----[definice novych intregracnich promennych vnitrni oblasti]-----
#-----[                     a vnejsi hranice                   ]-----

dx=Measure("dx",domain=mesh,subdomain_data=domains)
ds=Measure("ds",domain=mesh,subdomain_data=boundaries)

Toto přeindexování míry dx a ds se efektivně využije při formulaci variace (28) pro různé části oblasti \(\Omega\) a její hranice. Bez újmy na obecnosti bude variační forma (28) definovaná vcelku a následně pomocí UFL funkcí lhs a rhs rozdělena na pravou a levou část a vyřešena příkazem solve.

#-----[definice variacni formy]-----

F=(inner(a0*grad(u),grad(v))*dx(0)+inner(a1*grad(u),grad(v))*dx(1)
   -g_L*v*ds(1)-g_R*v*ds(3)
   -f*v*dx(0)-f*v*dx(1))

#-----[separace leve a prave strany rovnic]-----

a,L=lhs(F),rhs(F)

#-----[reseni problemu]-----

u=Function(V)
solve(a==L,u,bcs)

S řešením u se může dále pracovat. Např. vyčíslit její integrály nebo derivace. Nejdříve např. integrál z normálové složky gradientu z funkce \(u\) podél horní hranice.

#-----[vypocet integralu z gradientu podel horni hranice]-----

n=FacetNormal(mesh)
m1=dot(grad(u),n)*ds(2)
v1=assemble(m1)
print("\int grad(u)*n ds(2)=",v1)

Nebo integrál \(u\) nad oblastí \(\Omega_1\).

#-----[vypocet integralu z >u< nad oblasti]-----

m2=u*dx(1)
v2=assemble(m2)
print("\int u dx(1)=",v2)

Samozřejmě se výsledek může vykreslit - např. pro \(u\) a \(\nabla u\).

#-----[vykrelseni reseni >u< a jeho gradientu]-----

plot(u,title='u')
plt.show()
plot(grad(u),title="grad(u)")
plt.show()

#-----[vykresleni >u< a jeho x-ove souradnice ]-----
#-----[gradientu podel osy x pro y=0.3 a y=0.6]-----

#-----[gradient se dopocitava, proto se musi]-----
#-----[   promitnout do prostoru vectoru    ]-----
#-----[   Lagrangeovych polynomu 2. radu    ]-----

V_plot=VectorFunctionSpace(mesh,"CG",2)
gradu=project(grad(u),V_plot)

#-----[tim se z nej stane funkce souradnic (x,y)]-----

x1_plot,y1_plot=[],[]
u1_plot,gradu1_plot=[],[]
x2_plot,y2_plot=[],[]
u2_plot,gradu2_plot=[],[]

for v in vertices(mesh):
  x=v.point().x()
  y=v.point().y()
  if y>=0.6-0.008 and y<=0.6+0.008:
    x1_plot.append(x)
    u1_plot.append(u(x,y))
    gradu1_plot.append(gradu(x,y)[0])
  if y>=0.3-0.008 and y<=0.3+0.008:
    x2_plot.append(x)
    u2_plot.append(u(x,y))
    gradu2_plot.append(gradu(x,y)[0])

fig,ax=plt.subplots()
ax.plot(x1_plot,u1_plot,label="y=0.6")
ax.plot(x2_plot,u2_plot,label="y=0.3")
ax.set_xlabel("x")
ax.set_ylabel("u")
ax.legend(loc="best")

fig,ax=plt.subplots()
ax.plot(x1_plot,gradu1_plot,label="y=0.6")
ax.plot(x2_plot,gradu2_plot,label="y=0.3")
ax.set_xlabel("x")
ax.set_ylabel(r"$\nabla_xu$")
ax.legend(loc="best")

plt.show()

Grafické výstupy jsou následující (kliknutím se obrázky zobrazí v původní velikosti):

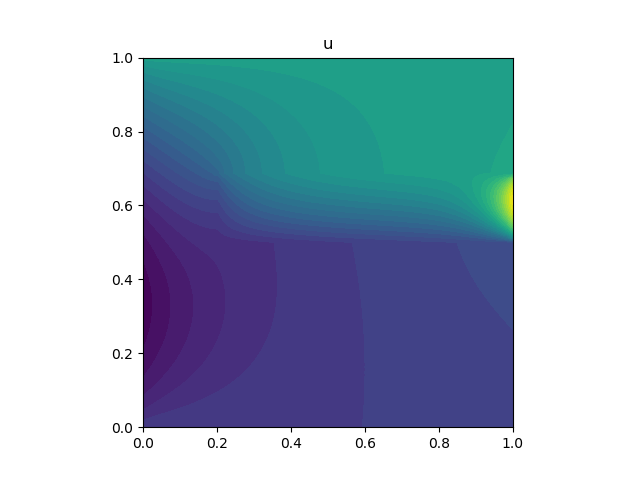
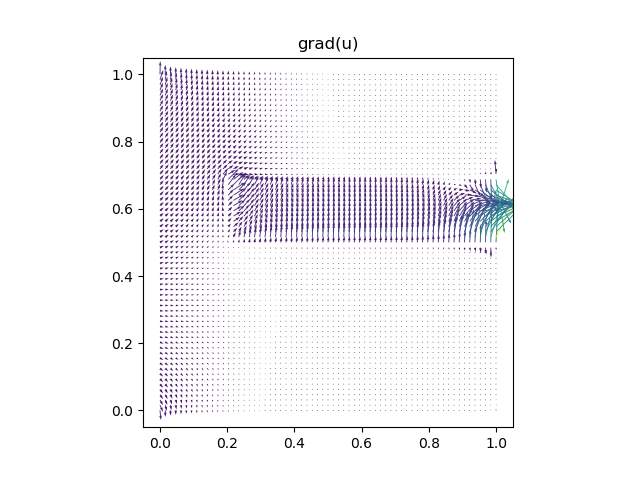
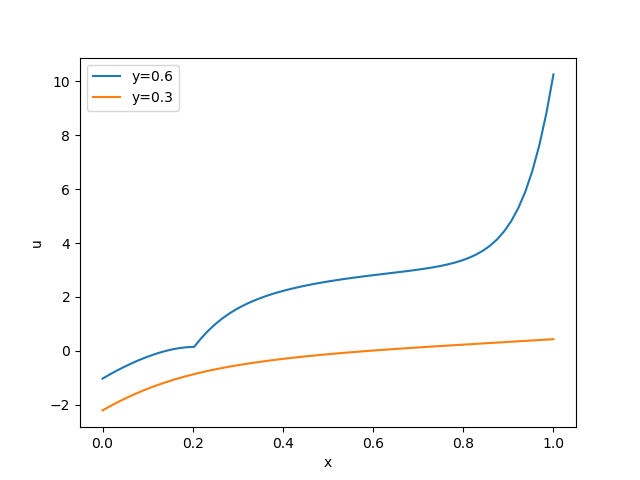
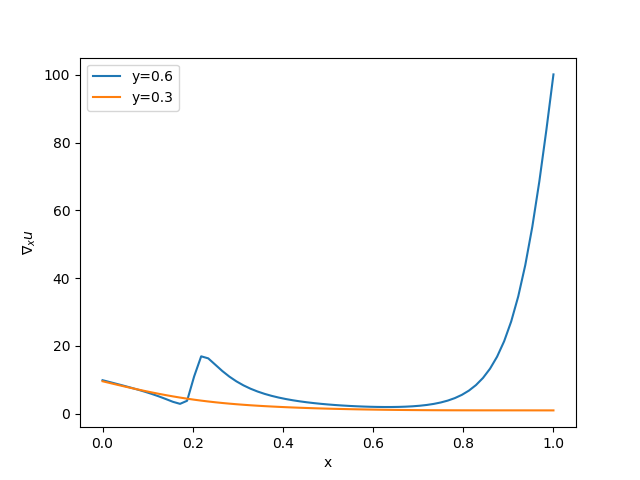
Výše popsaný skript lze stáhnout zde.

Implementace pomocí GMSH

Vytvoření diskretizace oblasti externím programem může značně zjednodušit manipulaci se značením podoblastí a hranic oblasti. Jedním z takových softwarů je volně stažitelný program GMSH, který dokáže vytvářet sítě dvou i třírozměrných oblastí, včetně indexování podoblastí a jejich hranic. Skript pro diskretizaci oblasti z úlohy (25) a (26) pomocí GMSH je následující.

Soubor se skriptem má příponu *.geo a může se vytvořit v externím textovém editoru nebo přímo v programu GMSH. Ve skriptu GMSH se mohou používat parametry, v tomto případě parametr lc, který bude znamenat délku hrany oblasti.

// Takhle se definuji promenne
lc=1;

Oblast \(\Omega\) se nadefinuje 12 body, které se propojí 17 čarami. Důvodem tolika čar je získání pěkné konečnoprvkové sítě. Každý bod je definovaný třemi souřadnicemi (první tři čísla v závorce) a parametrem nastavující hustotu sítě (čtvrtá číslice v závorce). Čím je tento parametr menší, tím je síť hustší. GMSH vždy začíná vytvářet síť od těchto bodů, kde je síť i nejhustší. Pro další účely se tento princip vytvoření konečnoprvkové sítě nevyužije, proto čtvrtý parametr každého bodu bude mít libovolnou (jednotkovou) hodnotu.

// prikaz >newp< vygeneruje nove cislo bodu,
// neni nutne to pouzivat, muze se pouzit
// rovnou kontkretni cislo. Prikaz >Point< definuje
// souradnice bodu a velikost elementu
// v danem bode (posledni hodnota)
p1=newp; Point(p1)={0,0,0,lc};
p2=newp; Point(p2)={0,lc,0,lc};
p3=newp; Point(p3)={lc,lc,0,lc};
p4=newp; Point(p4)={lc,0,0,lc};
p5=newp; Point(p5)={0.2*lc,0.5*lc,0,lc};
p6=newp; Point(p6)={0.2*lc,0.7*lc,0,lc};
p7=newp; Point(p7)={lc,0.7*lc,0,lc};
p8=newp; Point(p8)={lc,0.5*lc,0,lc};
p9=newp; Point(p9)={0,0.5*lc,0,lc};
p10=newp; Point(p10)={0,0.7*lc,0,lc};
p11=newp; Point(p11)={0.2*lc,0,0,lc};
p12=newp; Point(p12)={0.2*lc,lc,0,lc};

// prikaz >newl< vygeneruje nove cislo primky,
// neni nutne pouzit, muze se zadat konkterni cislo
// prikaz >Line< definuje caru ze dvou bodu,
// ktere jsou zadany svymi identifikacnimi body
l1=newl; Line(l1)={p1,p9};
l2=newl; Line(l2)={p9,p10};
l3=newl; Line(l3)={p2,p10};
l4=newl; Line(l4)={p2,p12};
l5=newl; Line(l5)={p3,p12};
l6=newl; Line(l6)={p3,p7};
l7=newl; Line(l7)={p7,p8};
l8=newl; Line(l8)={p4,p8};
l9=newl; Line(l9)={p4,p11};
l10=newl; Line(l10)={p1,p11};
l11=newl; Line(l11)={p5,p6};
l12=newl; Line(l12)={p6,p10};
l13=newl; Line(l13)={p6,p7};
l14=newl; Line(l14)={p5,p9};
l15=newl; Line(l15)={p5,p8};
l16=newl; Line(l16)={p5,p11};
l17=newl; Line(l17)={p6,p12};

Výsledek vypadá následovně (kliknutím se obrázek zvětší)

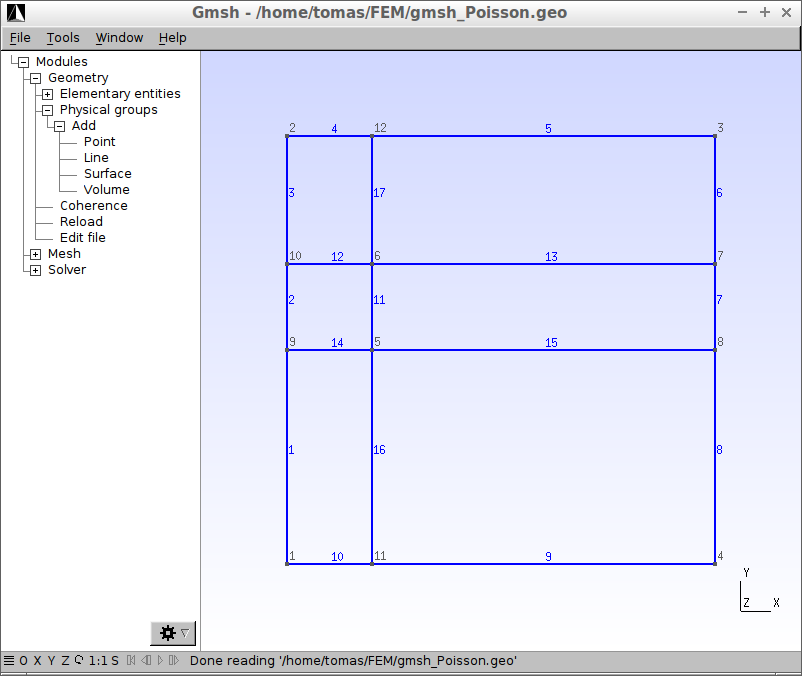
Plochy se vytvoří tak, že se jednotlivé čáry spojí v uzavřené smyčky příkazem Line Loop. Záporná hodnota čísla čáry znamená, že se daná čára orientuje v opačném smyslu, než byla definována příkazem Line. Plocha se nakonec vytvoří ze smyček čar, kde se opět může použít opačné znaménko čísla smyčky ke změně orientace dané smyčky.

// prikazem >Line Loop< a >Plane Surface< se vytvori
// rovinna plocha zaporna znamenka u cisel primek
// a plochy otaceji jejich orientaci
Line Loop(1)={l1,-l14,l16,-l10};
Line Loop(2)={-l16,l15,-l8,l9};
Line Loop(3)={l2,-l12,-l11,l14};
Line Loop(4)={l11,l13,l7,-l15};
Line Loop(5)={-l3,l4,-l17,l12};
Line Loop(6)={l17,-l5,l6,-l13};
Plane Surface(1)={1};
Plane Surface(2)={2};
Plane Surface(3)={3};
Plane Surface(4)={4};
Plane Surface(5)={5};
Plane Surface(6)={6};

Plochy vypadají následovně (kliknutím se obrázek zvětší)

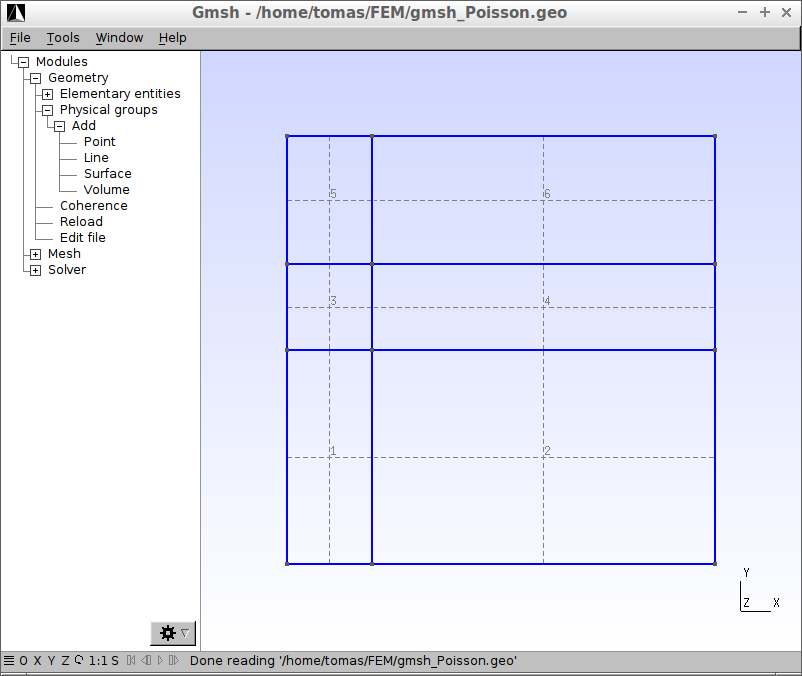
Protože je oblast \(\Omega\) velice jednoduchá, je žádoucí, aby byla i "inteligentně" diskretizovaná. Z tímto účelem je každá čára rozdělena konkrétním počtem bodů. Následně je příkazem Transfinite Surface konečnoprvková síť každé oblasti optimalizována.

// meschovani lze ovlivnit, napr. prikazem >Transfinite Line<,
// ktery rozdeli caru pravidelne pomoci urciteho
// poctu bodu (pocitaji se i krajni body)
Transfinite Line{l1}=33;
Transfinite Line{l2}=13;
Transfinite Line{l3}=21;
Transfinite Line{l4}=13;
Transfinite Line{l5}=53;
Transfinite Line{l6}=21;
Transfinite Line{l7}=13;
Transfinite Line{l8}=33;
Transfinite Line{l9}=53;
Transfinite Line{l10}=13;
Transfinite Line{l11}=13;
Transfinite Line{l12}=13;
Transfinite Line{l13}=53;
Transfinite Line{l14}=13;
Transfinite Line{l15}=53;
Transfinite Line{l16}=33;
Transfinite Line{l17}=21;

// prikaz >Transfinite Surface< doplni prikaz >Transfinite Line<
// a vytvori peknou sit
Transfinite Surface{1};
Transfinite Surface{2};
Transfinite Surface{3};
Transfinite Surface{4};
Transfinite Surface{5};
Transfinite Surface{6};

Konečnoprvková síť se vygeneruje příkazem 2D v menu Mesh. Výsledek je následující (kliknutím se obrázek zvětší).

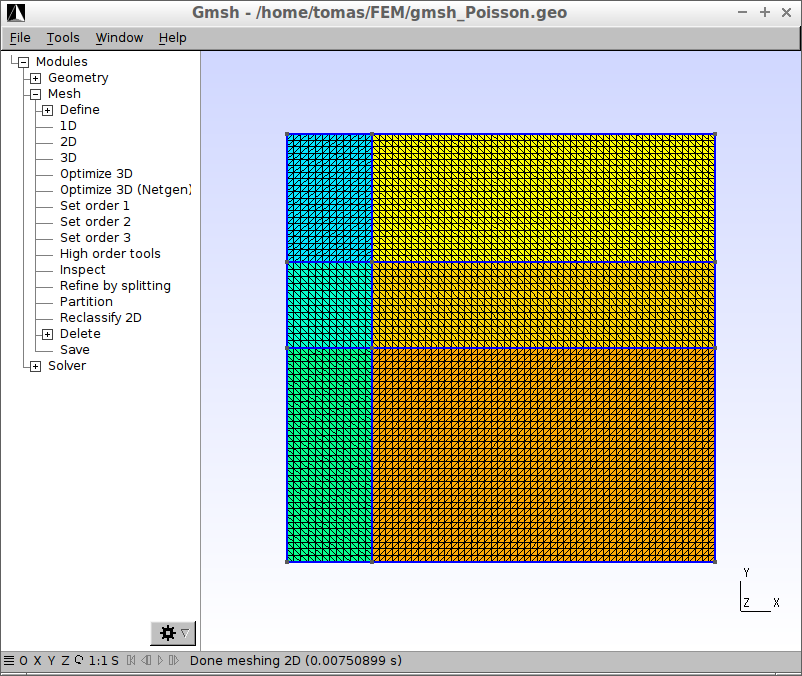
Nakonec se jednotlivé plochy a čáry hranice sloučí a očíslují indexy, které se fyzicky použijí ve FEniCSu.

// Prikazy >Physical Line< a >Physical Surface< priradi
// konkretni indexy lajnam a plocham
Physical Line(1)={l1,l2,-l3};
Physical Line(2)={l4,-l5};
Physical Line(3)={l6,l7,-l8};
Physical Line(4)={l9,-l10};
Physical Surface(0)={1,2,3,5,6};
Physical Surface(1)={4};

Po opětovném použití příkazu Mesh > 2D lze zobrazit upravené indexy jednotlivých oblastí a hranic prvků. Indexy jednotlivých částí vnější hranice oblasti \(\Omega\) jsou následující (kliknutím se obrázek zvětší)

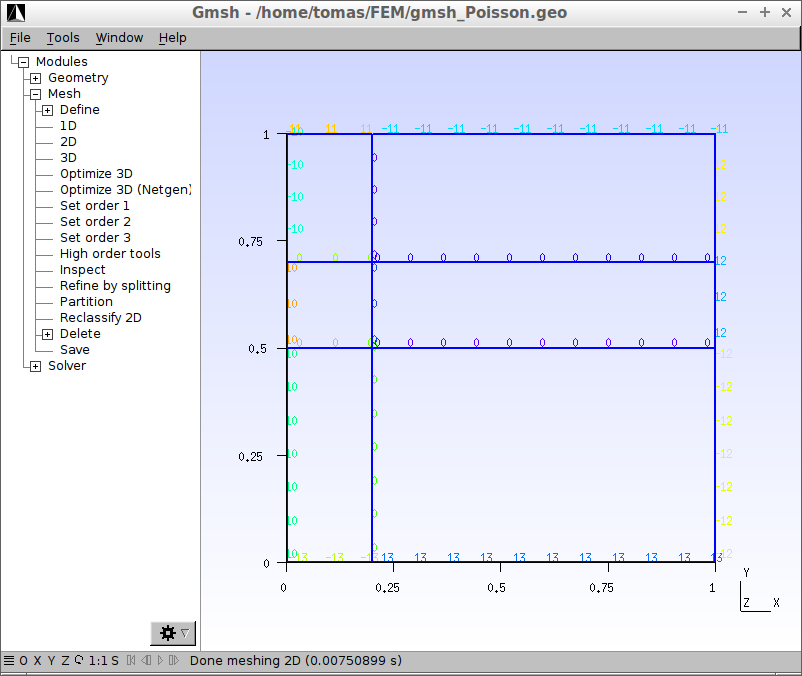
a indexy oblastí \(\Omega_0\) a \(\Omega_1\) jsou následující (kliknutím se obrázek zvětší)

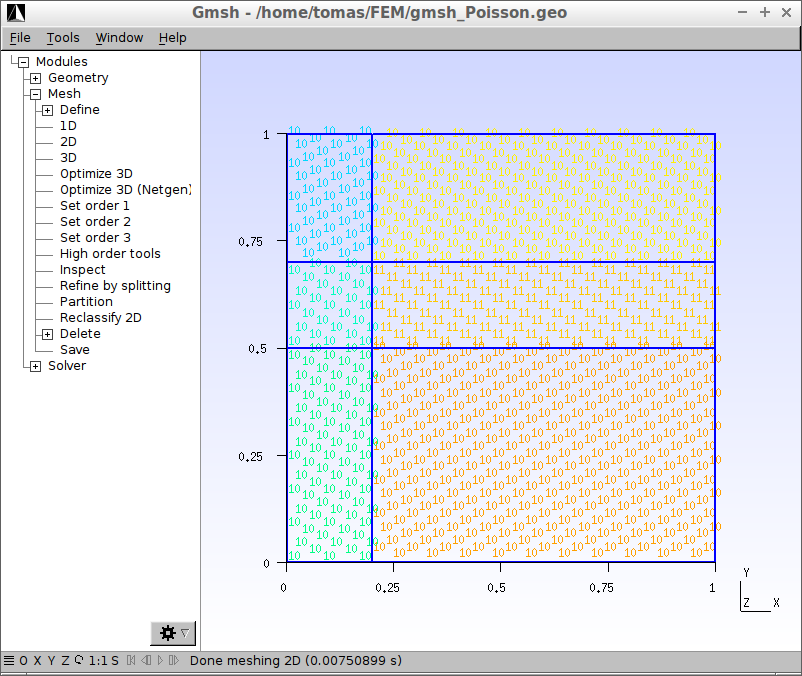
Příkazem Mesh > Save se diskretizovaná oblast uloží do souboru s příponou msh. Systém FEniCS naneštěstí tento formát neumí zpracovat. Užívá totiž svůj vlastní xml-formát. Pro konverzi msh-souboru do xml-souboru má FEniCS zabudovaný prográmek dolfin-convert, který se spouští v příkazovém řádku terminálu

uživatel$ dolfin-convert soubor.msh soubor.xml

Program dolfin-convert vytvoří tři xml-soubory: soubor.xml, soubor_facet_region.xml a soubor_physical_region.xml. První dává informaci o konečnoprvkové síti obecně, druhý a třetí obsahuje přiřazené fyzické indexy k hranám prvků na hranici oblasti a prvkům v oblasti \(\Omega_0\) a \(\Omega_1\).

Konečnoprvková síť vytvořená pomocí GMSH značně zjednodušuje samotný kód FEniCSu v Pythonu. Odpadá zde manipulace se sítí včetně indexování a označování prvků spadající do různých oblastí a částí hranic. Stačí tedy třídou Mesh načíst první z výše zmíněné trojice xml-souborů. Dále oblasti \(\Omega_0\) a \(\Omega_1\) a jednotlivé části hranice \(\Gamma\) jsou definovány ze zbývajících xml-souborů pomocí instancí domains a doundaries třídy MeshFunction.

from dolfin import *
import matplotlib.pyplot as plt

#-----[vymeshovani jednotkoveho ctverce]-----

mesh=Mesh('gmsh_Poisson.xml')

#-----[inicializovani vnitrku prvku vymeshovane oblasti]-----

domains=MeshFunction("size_t",mesh,'gmsh_Poisson_physical_region.xml')

#-----[inicializovani hran prvku vymeshovane oblasti]-----

boundaries=MeshFunction("size_t",mesh,'gmsh_Poisson_facet_region.xml')

#-----[vyber baze prostoru funkci definovaneho nad prvky]-----

V=FunctionSpace(mesh,"CG",2)

#-----[Definice vstupnich hodnot, prip. vyrazu]----

a0=Constant(1.0)
a1=Constant(0.01)

class MyExpression1(Expression):
  def eval(self,value,x):
    value[0]=-10*exp(-(x[1]-0.5)**2)

class MyExpression2(Expression):
  def eval(self,value,x):
    value[0]=1

#-----[instance vyrazu 1 a 2 na bazi prostoru funkci V]-----

g_L=MyExpression1(element=V.ufl_element())
g_R=MyExpression2(element=V.ufl_element())
f=MyExpression2(element=V.ufl_element())

#-----[definovani trial a testovaci funkce]-----

u=TrialFunction(V)
v=TestFunction(V)

#-----[definice Dirichletovych okrajovych podminek]-----
#-----[             podel hranice 2 a 4           ]-----

bcs=[DirichletBC(V,5.0,boundaries,2),
     DirichletBC(V,0.0,boundaries,4)]

#-----[definice novych intregracnich promennych vnitrni oblasti]-----
#-----[                     a vnejsi hranice                   ]-----

dx=Measure("dx",domain=mesh,subdomain_data=domains)
ds=Measure("ds",domain=mesh,subdomain_data=boundaries)

#-----[definice variacni formy]-----

F=(inner(a0*grad(u),grad(v))*dx(0)+inner(a1*grad(u),grad(v))*dx(1)
   -g_L*v*ds(1)-g_R*v*ds(3)
   -f*v*dx(0)-f*v*dx(1))

#-----[separace leve a prave strany rovnic]-----

a,L=lhs(F),rhs(F)

#-----[reseni problemu]-----

u=Function(V)
solve(a==L,u,bcs)

#-----[vypocet integralu z gradientu podel horni hranice]-----

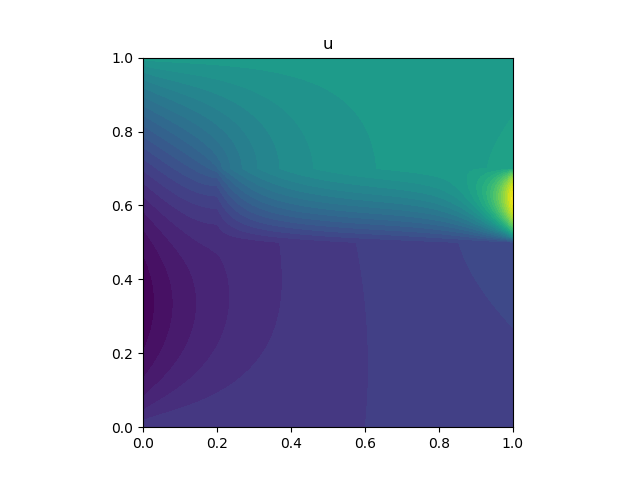
plot(u,title='u')
plt.show()

Vykreslení funkce \(u\) je totožné jako v případě bez použití GMSH z předchozího příkladu (kliknutím se obrázek zvětší)

Výše popsané skripty lze stáhnout zde a zde.

3D úlohy ohybu vetknutých prutů (FEniCS 2019.1.0)

Následující příklady demonstrují formulaci a řešení variačního 3D problému elasticity na příkladu vetknutých prutů zatížených ohybem.

Formulace problému

Cílem následujícího příkladu je nalézt slabé řešení pro tři úlohy pružnosi ohybu vetknutých prutů. Geometrie prutů je uvedena na obrázcích níže. Pruty jsou vetknuty na vzdálenějším konci. Na bližším konci jsou zatížené ohybem symbolickou měrnou silou o velikosti \(F=1\,\mathrm{N}\times\mathrm{mm}^{-2}\). Materiál prutů je \(E=2.1\times10^5\,\mathrm{MPa}\) a \(\nu=0.3\).

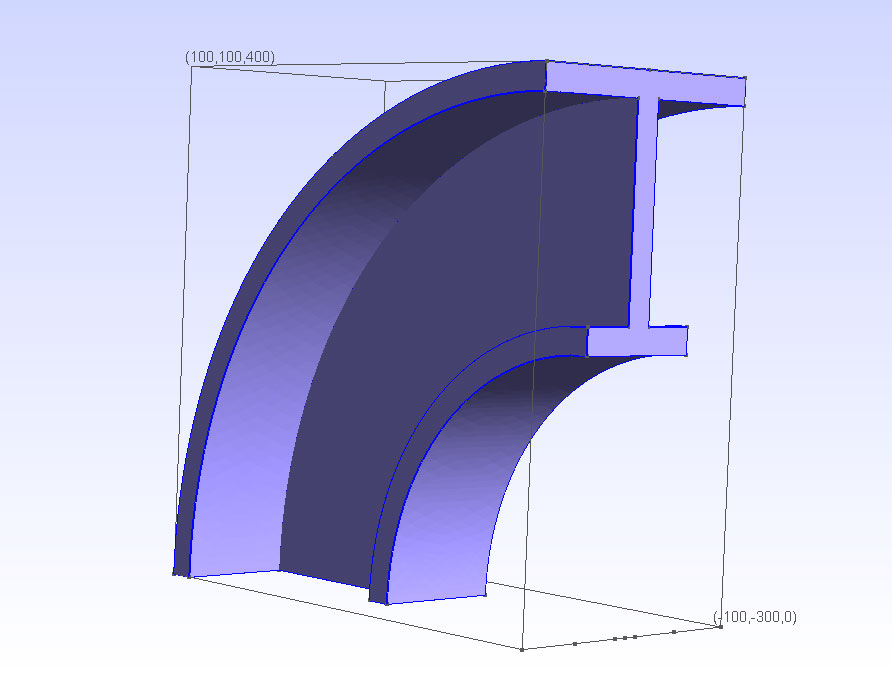
Příklad 1. Silně zakřivený prut.

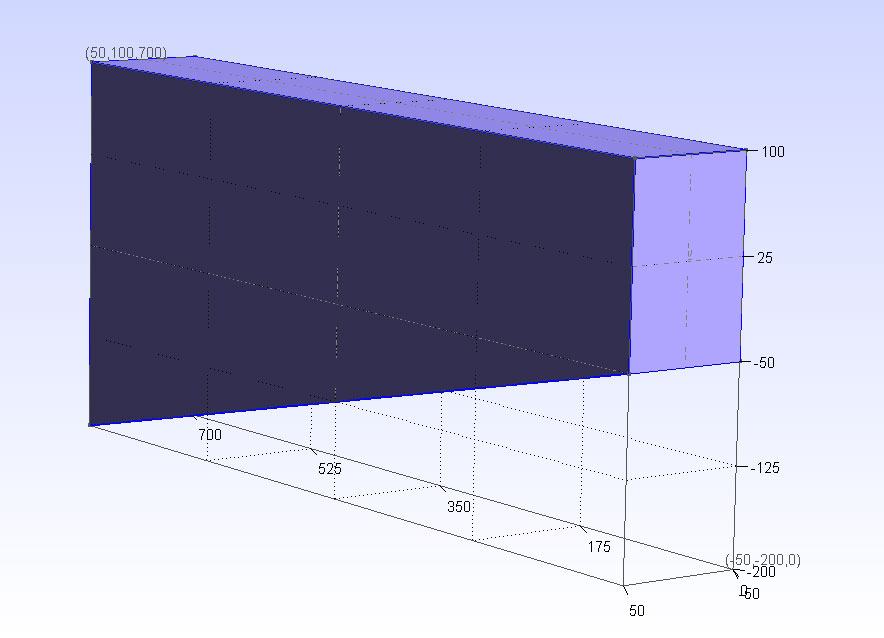
Příklad 2. Prut se spojitou změnou průřezu.

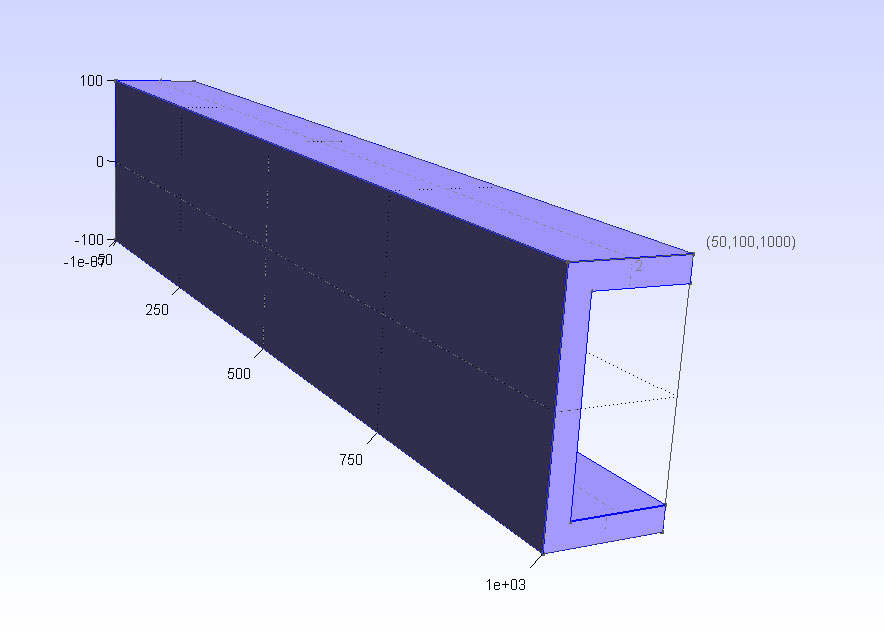
Příklad 3. Prut s nesymetrickým příčným průřezem.

Slabá formulace

Nechť je dán okrajový problém klasické isotropní elasticity daný rovnicemi rovnováhy a konstitutivními a kinematickými vztahy

(29)\[\nabla\cdot\boldsymbol{\sigma}=0\quad\mathrm{na}\,\Omega,\]

(30)\[\boldsymbol{\sigma}=\lambda\mathrm{tr}(\boldsymbol{\varepsilon})\boldsymbol{I} +2\mu\boldsymbol{\varepsilon},\]

(31)\[\boldsymbol{\varepsilon}=\frac{1}{2}(\nabla\boldsymbol{u}+\boldsymbol{u}\nabla),\]

kde \(\lambda\) a \(\mu\) jsou Lamého konstanty a \(\Omega\) je konečné těleso, které má na své hranici \(\partial\Omega=\partial\Omega_u\cup\partial\Omega_t\) za podmínky \(\Omega_u\cap\Omega_t=\emptyset\) předepsané buď Dirichletovy okrajové podmínky

(32)\[\boldsymbol{u}=\overline{\boldsymbol{u}}\quad\mathrm{na}\,\partial\Omega_u\]

nebo Neumannovy okrajové podmínky

(33)\[\boldsymbol{\sigma}\cdot{\boldsymbol{n}}=\overline{\boldsymbol{t}}\quad\mathrm{na}\,\partial\Omega_t.\]

Rovnice (29) se vynásobí libovolnou testovací funkcí, přesněji vektorem \(\boldsymbol{v}\), jehož fyzikální význam odpovídá tzv. virtuálním posuvům, a integruje se přes oblast \(\Omega\)

(34)\[\int_{\Omega}(\nabla\cdot\boldsymbol{\sigma})\cdot\boldsymbol{v}\mathrm{d}\Omega=0.\]

Integrál na levé straně (34) se může přepsat do tvaru

(35)\[\int_{\Omega}\nabla\cdot(\boldsymbol{\sigma}\cdot\boldsymbol{v})\mathrm{d}\Omega -\int_{\Omega}\boldsymbol{\sigma}:\nabla\boldsymbol{v}\mathrm{d}\Omega=0.\]

První integrál na levé straně (35) se může převést na plošný integrál

(36)\[\int_{\partial\Omega}\boldsymbol{n}\cdot\boldsymbol{\sigma}\cdot\boldsymbol{v}\mathrm{d}\partial\Omega -\int_{\Omega}\boldsymbol{\sigma}:\nabla\boldsymbol{v}\mathrm{d}\Omega=0\]

a za použití symboliky v okrajových podmínkách (33) se může přepsat do tvaru

(37)\[\int_{\Omega}\boldsymbol{\sigma}:\nabla\boldsymbol{v}\mathrm{d}\Omega =\int_{\partial\Omega_t}\overline{\boldsymbol{t}}\cdot\boldsymbol{v}\mathrm{d}\partial\Omega.\]

Tenzor \(\nabla\boldsymbol{v}\) lze rozepsat na symetrickou a antisymetrickou část

(38)\[\nabla\boldsymbol{v}=\boldsymbol{\varepsilon}(\boldsymbol{v})+\boldsymbol{\varepsilon}^{ns}(\boldsymbol{v}),\]

kde \(\boldsymbol{\varepsilon}(\boldsymbol{v})\) je ve fyzikálním smyslu deformace (31) a

(39)\[\boldsymbol{\varepsilon}^{ns}(\boldsymbol{v})=\frac{1}{2}(\nabla\boldsymbol{v}-\boldsymbol{v}\nabla).\]

Tenzor napětí \(\boldsymbol{\sigma}\) je symterický a ve skalárním součinu s nesymetrickou částí tenzoru \(\nabla\boldsymbol{v}\) v integrálu na levé straně (37) dává nulovou hondotu, tedy

(40)\[\boldsymbol{\sigma}:\boldsymbol{\varepsilon}^{ns}(\boldsymbol{v})=0.\]

Na základě tohoto faktu se může formulovat slabá formulace problému pružnosti jako nalezení takového vektoru posuvů \(\boldsymbol{u}\), aby splňoval následující variační problém

(41)\[\int_{\Omega}\boldsymbol{\sigma}(\boldsymbol{u}):\nabla\boldsymbol{\varepsilon}(\boldsymbol{v})\mathrm{d}\Omega =\int_{\partial\Omega_t}\overline{\boldsymbol{t}}(\boldsymbol{u})\cdot\boldsymbol{v}\mathrm{d}\partial\Omega,\]

a Dirichletovy okrajové podmínky

(42)\[\boldsymbol{u}=\overline{\boldsymbol{u}}\quad\mathrm{na}\,\partial\Omega_u,\]

kde samozřejmě v případě izotropního materiálu platí konstitutivní vztah (30). Nalezení řešení \(\boldsymbol{u}\) slabé formulace (41) není vůbec snadné, zejména v případě 3D úloh. Vhodné numerické metody k tomuto účelu jde spočítat na dvou prstech jedné ruky. Níže je uveden skript v Pythonu pro MKP řešič FEniCS, viz fenicsproject.org, skripty pro generování konečnoprvkové sítě modelů prutů v programu GMSH, viz gmsh.info, a výstupy z postprocesorového programu ParaView, viz paraview.org.

• Skript pro FEniCS v jazyce Python ke stažení zde.

• GMSH skript a jeho export do msh formátu pro příklad zakřiveného prutu ke stažení zde a zde.

• GMSH skript a jeho export do msh formátu pro příklad prutu se spojitým proměnným průřezem ke stažení zde a zde.

• GMSH skript a jeho export do msh formátu pro příklad prutu s nesymetrickým příčným průřezem ke stažení zde a zde.

Příklad 1. Tisíci násobně zvětšený průhyb silně zakřiveného vetknutého prutu.

Příklad 2. Tisíci násobně zvětšený průhyb vektnutého prutu se spojitě proměnným příčným průřezem.

Příklad 3. Tři sta násobně zvětšený průhyb prizmatického prutu s nesymetrickým příčným průřezem.