Výuka - dodatek I

Bettiho věta

Jedna z nejvýznamnějších vět v lineární pružnosti je Rayleigh-Bettiho věta, která může být formulována následovně,

Věta (Rayleigh-Betti): Nechť \(\Omega\) je elastické izotropní těleso s hranicí \(\partial\Omega\), které je ve statické rovnováze s vnějším působením dvou soustav objemových sil \(\big(F_x,F_y,F_z\big)\) a \(\big(\overline{F}_x,\overline{F}_y,\overline{F}_z\big)\) a plošných sil \(\big(f_x,f_y,f_z\big)\) a \(\big(\overline{f}_x,\overline{f}_y,\overline{f}_z\big)\). První soustava sil \(\big(F_x,F_y,F_z\big)\) a \(\big(f_x,f_y,f_z\big)\) vyvolává deformační posuvy \(\big(u,v,w\big)\), druhá soustava sil \(\big(\overline{F}_x,\overline{F}_y,\overline{F}_z\big)\) a \(\big(\overline{f}_x,\overline{f}_y,\overline{f}_z\big)\) vyvolává deformační posuvy \(\big(\overline{u},\overline{v},\overline{w}\big)\). Pak platí,

(1)\[\begin{split}\begin{equation} \begin{split} & \int_{\Omega}\big(F_x\overline{u}+F_y\overline{v}+F_z\overline{w}\big)\mathrm{d}V +\int_{\partial\Omega}\big(f_x\overline{u}+f_y\overline{v}+f_z\overline{w}\big)\mathrm{d}S \\ & =\int_{\Omega}\big(\overline{F}_xu+\overline{F}_yv+\overline{F}_zw\big)\mathrm{d}V +\int_{\partial\Omega}\big(\overline{f}_xu+\overline{f}_yv+\overline{f}_zw\big)\mathrm{d}S. \end{split} \end{equation}\end{split}\]

Jestliže jsou objemové, resp. plošné síly bodové, tj.

(2)\[\big(F_x,F_y,F_z\big)\equiv\big(f_x,f_y,f_z\big)\equiv\boldsymbol{P},\]

dostane se speciální případ Rayleigh-Bettiho věty,

Věta (Maxwellova): Nechť elastické izotropní těleso je ve statické rovnováze s vnějším působením dvou (objemových nebo plošných) sil \(\boldsymbol{P}_i\) a \(\boldsymbol{P}_j\), viz následující obrázek,

přičemž \(\big|\boldsymbol{P}_i\big|=\big|\boldsymbol{P}_j\big|=\big|\boldsymbol{P}\big|=P\). Síla \(\boldsymbol{P}_i\) vyvolává deformační posuv \(\big(\Delta_{ji}\big)_{n_2}\) ve směru nositelky \(n_2\) a místě působení \(j\) síly \(boldsymbol{P}_j\). Síla \(\boldsymbol{P}_j\) vyvolává deformační posuv \(\big(\Delta_{ij}\big)_{n_1}\) ve směru nositelky \(n_1\) a místě působení \(i\) síly \(\boldsymbol{P}_i\). Pak platí,

(3)\[A_{ij}=P_i\big(\Delta_{ij}\big)_{n_1}=P_j\big(\Delta_{ji}\big)_{n_2}=A_{ji},\]

nebo-li, protože \(P_i=P_j\),

(4)\[\big(\Delta_{ij}\big)_{n_1}=\big(\Delta_{ji}\big)_{n_2}.\]

Poznámka: V ještě speciálnějším případě, když se jedná o prut a průhyby prutu mají směr jako zatěžující osamělé síly, které jsou v tomto případě objemové, platí,

(5)\[A_{ij}=P_i\Delta_{ij}=P_j\Delta_{ji}=A_{ji},\]

nebo-li, protože \(P_i=P_j\),

(6)\[\Delta_{ij}=\Delta_{ji}.\]

Poznámka: V případě prutů se vyskytuje také liniové zatížení, které reprezentuje objemové síly \(\mathrm{d}\boldsymbol{F}=\big(0,0,q\mathrm{d}x\big)\) v místě \(i\), takže podle Rayleigh-Bettiho věty pro průhyb v místě působení jednotkové síly \(\boldsymbol{P}_j\) platí,

(7)\[\int_a^bq\Delta_{ij}\mathrm{d}l=\Delta_{ji}.\]

Greenova funkce pro prut na dvou podporách

K aplikaci Bettiho věty je nutné znát tzv. Greenovu funkci pro danou úlohu. V tomto případě půjde o úlohu prutu na dvou podporách. V pružnosti a pevnosti je Greenova funkce odezvou (průhybem) prutu na zatížení jednotkovou silou, jak ukazuje následující obrázek,

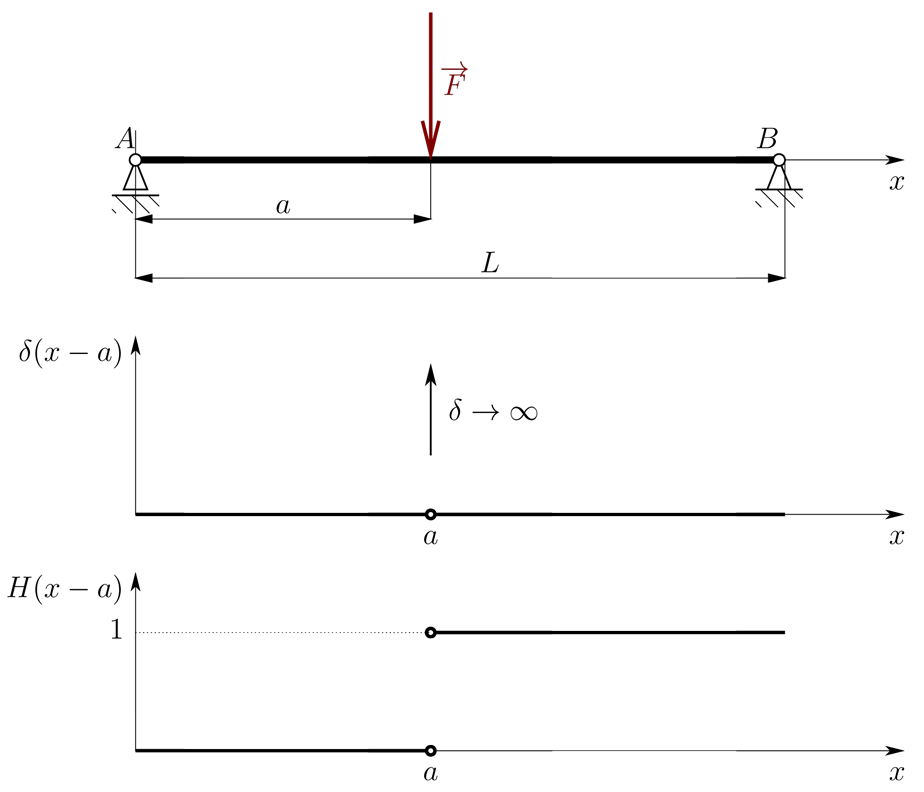
Takové zatížení se může zapsat následovně,

(8)\[\begin{split}q(x)=\delta(x-a)=\Big\{ \begin{array}{ccc} 0 & \mathrm{pro} & x\neq a,\\ \infty & \mathrm{pro} & x=a, \end{array}\end{split}\]

kde \(\delta\left(x-a\right)\) je tzv. "delta" funkce, která (ač to není možné) je symbolicky vykreslena na druhém obrázku výše. Delta funkce má všude nulovou hodnotu, v bodě \(a\) nabývá hodnoty rostoucí nad všechny meze. Má však také následující důležitou vlastnost,

(9)\[\int_{-\infty}^{\infty}q(x-a)\mathrm{d}x=1.\]

Pro průhybovou čáru prutu pak platí diferenciální rovnice,

(10)\[EJw^{(IV)}(x)=q(x),\]

která po dosazení (9) má tvar,

(11)\[EJw^{(IV)}(x)=\delta(x-a),\]

kde \(E\) je Youngův modul pružnosti v tahu a \(J\) je kvadratický modul průřezu. Integrací se dostane,

(12)\[EJw^{\prime\prime\prime}(x)=H(x-a)+C_1,\]

kde \(H(x-a)\) je tzv. Heavy-sideová funkce (9) (viz třetí graf na obrázku výše), pro kterou platí,

(13)\[\begin{split}H(x)=\int_{-\infty}^x\delta\big(\xi\big)\mathrm{d}\xi=\Big\{ \begin{array}{ccc} 0 & \mathrm{pro} & x<0,\\ 1 & \mathrm{pro} & x>0, \end{array}\end{split}\]

resp.

(14)\[\begin{split}H(x-a)=\int_{-\infty}^x\delta\big(\xi-a\big)\mathrm{d}\xi=\Big\{ \begin{array}{ccc} 0 & \mathrm{pro} & x<a,\\ 1 & \mathrm{pro} & x>a. \end{array}\end{split}\]

Další integrací (12) se dostane,

(15)\[\begin{split}\begin{equation} \begin{split} EJw^{\prime\prime}(x) =& (x-a)H(x-a)+C_1x+C_2, \\ EJw^{\prime}(x) =& \frac{1}{2}(x-a)^2H(x-a)+\frac{1}{2}C_1x^2+C_2x+C_3, \\ EJw(x) =& \frac{1}{6}(x-a)^3H(x-a)+\frac{1}{6}C_1x^3+C_2\frac{1}{2}x^2+C_3x+C_4.\label{eq:w} \end{split} \end{equation}\end{split}\]

Konstanty \(C_1-C_4\) se stanoví z okrajových podmínek,

(16)\[\begin{split}\begin{equation} \begin{split} w(0) =& 0, \\ EJw^{\prime\prime}(0) =& 0, \\ w(L) =& 0, \\ EJw^{\prime\prime}(L) =& 0, \end{split} \end{equation}\end{split}\]

které vedou na soustavu rovnic,

(17)\[\begin{split}\begin{equation} \begin{split} C_2 =& 0,\\ C_4 =& 0,\\ (L-a)+C_1L+C_2 =& 0,\\ \frac{1}{6}(L-a)^3+\frac{1}{6}C_1L^3+C_2\frac{1}{2}L^2+C_3L+C_4 =& 0. \end{split} \end{equation}\end{split}\]

Jejich řešením je,

(18)\[C_1=-\frac{L-a}{L},\quad C_2=0,\quad C_3=\frac{a(L-a)(2L-a)}{6L},\quad C_4=0.\]

Tzv. Greenova funkce je pak podle (15) průhyb po dosazení konstant (18), tedy

(19)\[\begin{split}\begin{equation} \begin{split} G\big(x,\xi\big)=w(x)\big|_{a=\xi}=& \frac{1}{6EJ}\bigg[(x-\xi)^{3}H\big(x-\xi\big) \\ & +\frac{L-\xi}{L}\big(-x^2+2\xi L-\xi^2\big)x\bigg]. \end{split} \end{equation}\end{split}\]

Tedy, jak bylo již poznamenáno výše, Greenova funkce nám dává hodnotu průhybu daného prutu libovolném bodě při daných okrajových podmínkách (uložení prutu) a zatížení jednotkovou osamělou silou.

Aplikace Rayleigh-Bettiho věty a Greenovy funkce na konkrétní příklad prutu na dvou podporách

Jestliže chceme znát průhybovou čáru prutu na dvou podporách, libovolně zatíženého, např. jak je uvedeno na obrázku,

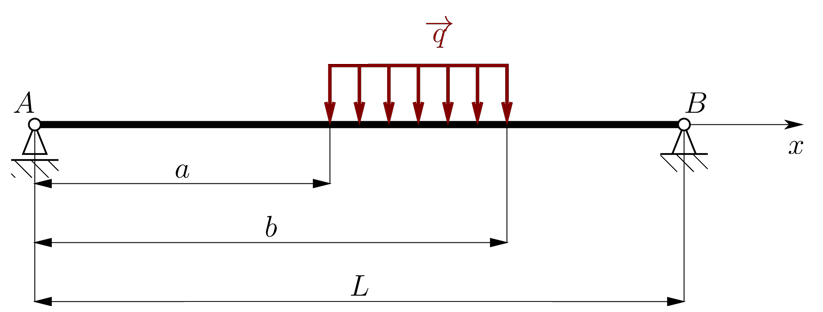
a známe odpovídající Greenovu funkci pro prut na dvou podporách, můžeme k tomuto účelu využít Rayleigh-Bettiho věty. Nejdříve je nutné vyjádřit statickou rovnováhu prutu odstraněním symbolů vazeb a jejich nahrazením odpovídajícími reakcemi \(F_A\) a \(F_B\), které vyjádříme z rovnic statické rovnováhy. Liniové zatížení \(q(x)=q\) v tomto případě reprezentuje objemové zatížení, reakce ve vazbách \(F_A\) a \(F_B\) zatížení plošné. Pak na základě výše zmíněných poznámek pro průhyb v prutu v libovolném bodě platí,

(20)\[w\big(\xi\big)=\int_a^bq(x)G\big(x,\xi\big)\mathrm{d}x+F_AG\big(0,\xi\big) +F_BG\big(L,\xi\big).\]

Podrobněji, Greenova funkce reprezentuje průhyb \(\Delta_{ij}\) v místě \(i=x\) od jednotkové síly \(P_j\) působící v místě \(j=\xi\). A Rayleigh-Bettiho věta pak dokáže s její pomocí vyjádřit průhyb \(\Delta_{ji}=w\big(\xi\big)\) v místě \(j=\xi\) působení síly \(P_j\), který je způsobený liniovým zatížením \(q\) a reakcemi ve vazbách \(F_A\) a \(F_B\). Protože působiště síly \(P_j\) je libovolné, dostaneme tak po integraci a faktu, že \(G\big(0,\xi\big)=G\big(L,\xi\big)=0\), tvar celé průhybové čáry,

(21)\[\begin{split}\begin{equation} \begin{split} w\big(\xi\big)=&\frac{q}{24EJL}\bigg\{ \big(L-\xi\big)\Big[\big(b^4-a^4\big) +2\big(\xi^2-2L\xi\big)\big(b^2-a^2\big)\Big] \\ &-L\Big[\big(b-\xi\big)^4H\big(b-\xi\big) -\big(a-\xi\big)^4H\big(a-\xi\big)\Big]\bigg\}. \end{split} \end{equation}\end{split}\]

Poznámka: Vztah (20) není korektně zapsán, stačí ho psát pouze ve tvaru,

(22)\[w\big(\xi\big)=\int_a^bq(x)G\big(x,\xi\big)\mathrm{d}x.\]

Součiny \(F_AG\big(0,\xi\big)\) a \(F_BG\big(L,\xi\big)\) ve vztahu (20) je totiž zbytečné uvádět, protože vliv reakcí \(F_A\) a \(F_B\) je již zahrnut v samotné Greenově funkci \(G\big(x,\xi\big)\), jelikož byla sestrojena pro prut na dvou podporách. Výrazy \(F_AG\big(0,\xi\big)\) a \(F_BG\big(L,\xi\big)\) ve vztahu (20) jsou uvedeny pouze ilustračně, aby bylo vidět, jak se může zacházet s osamělými silami jako vnějším zatížením prutu.

Poznámka: Sestrojení Greenovy funkce může být velmi komplikovaný nebo dokonce neřešitelný problém, zejména pro dvoudimenzionální a třídimenzionální úlohy. Proto se funkce \(G\big(x,\xi\big)\) často hledá pro jednoduché oblasti tvaru kruhu, koule nebo dokonce nekonečné oblasti. To platí i pro pruty, kde funkce \(G\big(x,\xi\big)\) může být obecně sestrojena pro nekonečně dlouhý prut. Toto zobecnění však vyžaduje zápis průhybu prutu \(w\big(\xi\big)\) ve tvaru (20). Pak jsou v něm ale síly \(F_A\) a \(F_B\) neznámé a musí se určit z okrajové podmínky nulového průhybu prutu na jeho koncích, tj. okrajových podmínek (16). V takovém případě již nehovoříme o Greenově funkci \(G\big(x,\xi\big)\), ale o tzv. fundamentálním řešení a metoda stanovení hodnot \(F_A\), \(F_B\) a průhybu \(w\big(\xi\big)\) v libovolném bodě střednice prutu se nazývá metoda integrálních rovnic nebo metoda hraničních prvků.

Termodynamika deformace

Z rovnice rovnováhy,

(23)\[\frac{\partial\sigma_{ik}}{\partial x_k}+F_i=0,\]

kde \(F_i\) je objemová síla a \(\sigma_{ik}\) je tenzor napětí, se dostane,

(24)\[F_i=\frac{\partial\sigma_{ik}}{\partial x_k}.\]

Zde, jako i v dalším, bude používána Einsteinova sumační symbolika. Roznásobením předchozí rovnice nenulovým posuvem \(\delta u_i\) a její integrací přes celý objem daného tělesa se dostane práce \(R\) vnitřních sil \(F_i\) (napětí) na posuvu \(\delta u_i\),

(25)\[\int\delta R\mathrm{d}V=\int\frac{\partial\sigma_{ik}}{\partial x_k}\delta u_i\mathrm{d}V.\]

Integrand \(\delta R\) je práce na jednotku objemu. Integrací předchozího integrálu po částech (per partes) se dostane,

(26)\[\int\delta R\mathrm{d}V=\oint\sigma_{ik}\delta u_i\mathrm{d}f_k -\int\sigma_{ik}\frac{\partial\delta u_i}{\partial x_k}\mathrm{d}V,\]

kde \(f_k\) je plocha povrchu daného tělesa. Tento vztah musí platit i pro neomezeně velké v nekonečnu nedeformované (jinak to nejde, protože by napětí v tělese muselo být nekonečně) těleso, jehož plocha povrchu je nekonečně velká. Pak je i napětí \(\sigma_{ik}\) na povrchu nulové a celý první integrál na pravé straně v (26) zmizí. Pak s využitím symetrie tenzoru napětí \(\sigma_{ik}\) platí,

(27)\[\begin{split}\begin{equation} \begin{split} \int\delta R\mathrm{d}V =& -\frac{1}{2}\int\sigma_{ik}\left(\frac{\partial\delta u_i}{\partial x_k} +\frac{\partial\delta u_k}{\partial x_i}\right)\mathrm{d}V \\ =& -\frac{1}{2}\int\sigma_{ik}\delta\left(\frac{\partial u_i}{\partial x_k} +\frac{\partial u_k}{\partial x_i}\right)\mathrm{d}V \\ =& -\int\sigma_{ik}\delta\varepsilon_{ik}\mathrm{d}V \end{split} \end{equation}\end{split}\]

a odkud plyne

(28)\[\delta R=-\sigma_{ik}\delta\varepsilon_{ik}.\]

V dalším budeme předpokládat, že elastická změna tělesa probíhá dostatečně pomalu a pozvolně, že se těleso bude vždy nacházet v termodynamické rovnováze a termodynamicky vratném stavu. Zavedeme měrné termodynamické veličiny typu entropie \(S\) nebo vnitřní energii \(\mathcal{E}\) vztažené na jednotku, jak je v pružnosti zvykem, nedeformovaného objemu. Nedeformovanost je důležitá vzhledem k tomu, že při elastické deformaci se objem mění. Pak pro změnu vnitřní energie \(\mathrm{d}\mathcal{E}\) platí,

(29)\[\mathrm{d}\mathcal{E}=T\mathrm{d}S-\mathrm{d}R=T\mathrm{d}S+\sigma_{ik}\mathrm{d}\varepsilon_{ik}.\]

V dalším bude třeba také znalost energetických poměrů v tělese při změně (nezměně) teploty, proto si zavedeme také tzv. volnou energii,

(30)\[F=\mathcal{E}-TS,\]

odkud se po dosazení za \(\mathcal{E}\) dostane,

(31)\[\mathrm{d}F=\mathrm{d}\mathcal{E}-S\mathrm{d}T-T\mathrm{d}S=-S\mathrm{d}T +\sigma_{ik}\mathrm{d}\varepsilon_{ik}.\]

Nakonec bude zajímavá také závislost energie na změně deformace \(\varepsilon_{ik}\), která se získá zavedením termodynamického potenciálu,

(32)\[\Phi=\mathcal{E}-TS-\sigma_{ik}\varepsilon_{ik}=F-\sigma_{ik}\varepsilon_{ik}\]

a jeho diferenciálu,

(33)\[\begin{split}\begin{equation} \begin{split} \mathrm{d}\mathrm{\Phi} =& \mathrm{d}F-\varepsilon_{ik}\mathrm{d}\sigma_{ik} -\sigma_{ik}\mathrm{d}\varepsilon_{ik} \\ =& -S\mathrm{d}T-\varepsilon_{ik}\mathrm{d}\sigma_{ik}. \end{split} \end{equation}\end{split}\]

Nyní se mohou vyjádřit napětí při konstantní entropii \(S\) (tepelně izolované těleso) nebo konstantní teplotě \(T\),

(34)\[\sigma_{ik}= \bigg(\frac{\partial\mathcal{E}}{\partial\varepsilon_{ik}}\bigg)\bigg|_{S} = \bigg(\frac{\partial F}{\partial\varepsilon_{ik}}\bigg)\bigg|_{T}.\]

Podobně se může vyjádřit deformace \(\varepsilon_{ik}\) při konstantní teplotě \(T\),

(35)\[\varepsilon_{ik}=-\bigg(\frac{\partial\Phi}{\partial\sigma_{ik}}\bigg)\bigg|_{T}.\]

Hookeův zákon

V pružnosti je nezbytná znalost závislosti napětí \(\sigma_{ik}\) na změně deformace \(\varepsilon_{ik}\). Nejdříve budeme předpokládat, že dané těleso je deformované při konkrétní teplotě, která se nemění a je konstantní v celém tělese. A dále, že je nedeformované při stejné teplotě, tedy že při této teplotě a při \(\varepsilon_{ik}=0\) v něm zmizí veškerá napětí, tj. \(\sigma_{ik}=0\). Dalším předpokladem je, že deformace \(\varepsilon_{ik}\) jsou malé, proto se mohou v blízkosti nuly rozložit v asymptotický rozvoj. Protože

(36)\[\sigma_{ik}=\frac{\partial F}{\partial\varepsilon_{ik}},\]

musí, na základě výše uvedených předpokladů (zejména nulové hodnoty \(\sigma_{ij}\) při nulové hodnotě \(\varepsilon_{ij}\)), z tohoto asymptotického rozvoje zmizet lineární členy. Ze symetrického tenzoru druhého řádu lze sestavit pouze dva nezávislé kvadratické skalární veličiny, \(\varepsilon_{ll}^2\) a \(\varepsilon_{ik}\varepsilon_{ik}\), a protože v lineární pružnosti je samozřejmě závislost mezi napětím a deformací maximálně lineární, je nejobecnější tvar volné energie následující,

(37)\[F=F_0+\frac{\lambda}{2}\varepsilon_{ll}^2+\mu\varepsilon_{ik}\varepsilon_{ik},\]

kde \(\lambda\) a \(\mu\) jsou tzv. Lamého konstanty, které mají k Youngovu modulu \(E\) a Poissonovu číslu \(\nu\) vztah

(38)\[\lambda=\frac{E\nu}{(1-2\nu)(1+\nu)},\quad\mu=\frac{E}{2(1+\nu)}.\]

Tenzor deformace se může také napsat ve tvaru,

(39)\[\varepsilon_{ik}=\bigg(\varepsilon_{ik}-\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg) +\frac{1}{3}\delta_{ik}\varepsilon_{ll},\]

kde \(\delta_{ik}\) je tzv. Kroneckerův delta symbol, pro který platí,

(40)\[\begin{split}\delta_{ik}=\Big\{ \begin{array}{ccc} 1 & \mathrm{pro} & i=k,\\ 0 & \mathrm{pro} & i\neq k. \end{array}\end{split}\]

Výraz

(41)\[\frac{1}{3}\delta_{ik}\varepsilon_{ll}\]

odpovídá objemové změně. Podle (39) se volná energie může psát ve tvaru (konstantní člen \(F_0\) anulujeme, bez újmy na obecnosti, odpovídá vlastní volné energii nedeformovaného tělesa),

(42)\[\begin{split}\begin{equation} \begin{split} F =& \frac{\lambda}{2}\varepsilon_{ll}^2 \\ & +\mu\bigg[\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg) +\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg] \bigg[\bigg(\varepsilon_{ik}-\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg) +\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg] \\ =& \frac{\lambda}{2}\varepsilon_{ll}^2 \\ & +\mu\bigg[\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)^2 +\frac{2}{3}\delta_{ik}\varepsilon_{ll}\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg) +\bigg(\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)^2\bigg] \\ =& \frac{\lambda}{2}\varepsilon_{ll}^2+\mu\bigg[\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)^2 +\frac{2}{3}\varepsilon_{ll}^2-\frac{2}{3}\varepsilon_{ll}^2 +\frac{1}{3}\varepsilon_{ll}^2\bigg] \\ =& \frac{\lambda}{2}\varepsilon_{ll}^2+\mu\bigg[\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)^2 +\frac{1}{3}\varepsilon_{ll}^2\bigg] \\ =& \mu\bigg(\varepsilon_{ik}-\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)^2 +\frac{K}{2}\varepsilon_{ll}^{2}, \end{split} \end{equation}\end{split}\]

kde \(\mu\) je modul pružnosti ve smyku a \(K\) je objemový modul stlačitelnosti,

(43)\[K=\lambda+\frac{2}{3}\mu.\]

Když je těleso v termodynamické rovnováze, nabývá volná energie svého minima, dokonce i v případě nedeformovaného tělesa, tj. když \(\varepsilon_{ik}=0\). Avšak, v případě nedeformovaného tělesa je \(F=0\). Odtud a z toho, že \(F\) je kvadratická forma plyne, že volná energie je pozitivně definitní a

(44)\[K>0\quad\mathrm{a}\quad\mu>0.\]

Pro diferenciál \(\mathrm{d}F\) platí

(45)\[\begin{split}\begin{equation} \begin{split} \mathrm{d}F =& K\varepsilon_{ll}\mathrm{d}\varepsilon_{ll}+2\mu\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)\mathrm{d}\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)\\ =& K\varepsilon_{ll}\mathrm{d}\varepsilon_{ll}+2\mu\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)\mathrm{d}\varepsilon_{ik} -\frac{2}{3}\mu\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)\mathrm{d}\big(\delta_{ik}\varepsilon_{ll}\big)\\ =& K\varepsilon_{ll}\mathrm{d}\varepsilon_{ll}+2\mu\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)\mathrm{d}\varepsilon_{ik} -\frac{2}{3}\mu\big(\varepsilon_{ll}\mathrm{d}\varepsilon_{ll} -\varepsilon_{ll}\mathrm{d}\varepsilon_{ll}\big)\\ =& K\varepsilon_{ll}\delta_{ik}\mathrm{d}\varepsilon_{ik} +2\mu\bigg(\varepsilon_{ik}-\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)\mathrm{d}\varepsilon_{ik}\\ =& \bigg[K\varepsilon_{ll}\delta_{ik}+2\mu\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)\bigg]\mathrm{d}\varepsilon_{ik}. \end{split} \end{equation}\end{split}\]

Podle (34) platí

(46)\[\sigma_{ik}=\frac{\partial F}{\partial\varepsilon_{ik}}=K\varepsilon_{ll}\delta_{ik} +2\mu\bigg(\varepsilon_{ik}-\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg).\]

Protože odtud po zúžení indexů \(i\) a \(k\) plyne

(47)\[\sigma_{ll}=3K\varepsilon_{ll}\]

a opětovným dosazením tohoto výrazu do (46) se dostane,

(48)\[\varepsilon_{ik}=\frac{1}{9K}\delta_{ik}\sigma_{ll}+\frac{1}{2\mu}\left(\sigma_{ik} -\frac{1}{3}\sigma_{ll}\delta_{ik}\right),\]

což je tzv. Hookeův zákon. S Hookeovým zákonem si můžeme ještě pohrát. Protože je volná energie \(F\) kvadratická forma, platí pro ni (tzv. Eulerova věta),

(49)\[\varepsilon_{ik}\frac{\partial F}{\partial\varepsilon_{ik}}=2F.\]

Protože

(50)\[\sigma_{ik}=\frac{\partial F}{\partial\varepsilon_{ik}},\]

platí podle (49) pro volnou energii následující důležitý vztah,

(51)\[F=\frac{\sigma_{ik}\varepsilon_{ik}}{2}.\]

Za \(\varepsilon_{ik}\) se může dosadit Hookeův zákon (48) a dostane se kvadratická forma vzhledem k \(\sigma_{ik}\). Aplikací Eulerovy věty se dostane

(52)\[\sigma_{ik}\frac{\partial F}{\partial\sigma_{ik}}=2F\]

a porovnáním s (51) se získá

(53)\[\varepsilon_{ik}=\frac{\partial F}{\partial\sigma_{ik}}.\]

Je však třeba si uvědomit, že zatímco (50) je prostý důsledek tvaru a existence volné energie, výraz (53) existuje jen díky a na základě platnosti Hookeova zákona (48).

Deformace se změnou teploty

Nyní se bude předpokládat, že při libovolné teplotě \(T\) se těleso dodatečně deformuje i při nulovém zatížení. Tato deformace však mizí při teplotě \(T_0\). Proto na rozdíl od předchozího případu se musí ve výrazu pro volnou energii (37) objevit také člen lineární vzhledem k deformaci \(\varepsilon_{ik}\). Avšak z tenzoru deformace lze sestavit jedinou lineární skalární veličinu \(\varepsilon_{ll}\), tj. součet jeho diagonálních prvků. Dále se bude předpokládat, že změna lineární části volné energie vzhledem ke změně teploty \(T-T_0\) je malá a této změně proporcionální, přičemž musí být anulována pro teplotu \(T=T_0\). Takže pro volnou energii závisející na teplotě \(T\) platí podle (42),

(54)\[F(T) = F_0(T)-K\alpha\big(T-T_0\big)\varepsilon_{ll}+ \mu\bigg(\varepsilon_{ik}-\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg)^2 +\frac{K}{2}\varepsilon_{ll}^2.\]

Koeficienty \(K\), \(\mu\) a \(\alpha\) jsou konstanty a jejich závislost na teplotě odpovídá veličinám malosti vyššího řádu, které zanedbáme. Derivací (54) podle \(\varepsilon_{ik}\) se dostane vztah pro napětí,

(55)\[\sigma_{ik}=-K\alpha\big(T-T_0\big)\delta_{ik}+K\varepsilon_{ll}\delta_{ik} +2\mu\bigg(\varepsilon_{ik}-\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg).\]

Zahřátí tělesa bez účasti vnějšího zatížení se projeví jeho nenulovou deformací a vymizením napětí, tedy

(56)\[0=K\big[-\alpha\big(T-T_0\big)+\varepsilon_{ll}\big]\delta_{ik}+2\mu\bigg(\varepsilon_{ik} -\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg).\]

Odtud plyne, že \(\varepsilon_{ik}=konst\cdot\delta_{ik}\), přičemž

(57)\[\varepsilon_{ll}=\alpha\big(T-T_0\big).\]

Protože \(\varepsilon_{ll}\) je úměrné objemové změně materiálu, koeficient \(\alpha\) představuje teplotní objemovou roztažnost. Dále při izotermické deformaci se teplota nemění a první člen pro \(T=T_0\) zmizí a pro volnou energii \(F\) se dostane základní vztah (42). Proto se koeficienty \(K\) a \(\mu\) nazývají izotermické moduly.

Předpokládejme, že je těleso dokonale izolováno od svého okolí (adiabatický děj). Při čistě tepelném zatížení tělesa se změní pouze jeho objem podle (57) aniž by se to nějak projevilo na stavu napětí v tělese. Jestliže se těleso navíc nějak zatíží podle předepsaných okrajových podmínek, generuje se při adiabatické deformaci napětí podle Hookeova zákona, viz (46),

(58)\[\sigma_{ik}=K_{ad}\varepsilon_{ll}\delta_{ik} +2\mu\bigg(\varepsilon_{ik}-\frac{1}{3}\delta_{ik}\varepsilon_{ll}\bigg),\]

kde na základě (55) pro \(K_{ad}\) platí

(59)\[K_{ad}=K\bigg[-\frac{\alpha\big(T-T_0\big)}{\varepsilon_{ll}}+1\bigg].\]

Modul \(K_{ad}\) je adiabatický a nahradil izotropní \(K\). První člen v závorce v \(K_{ad}\) není roven mínus jedné, protože objemová změna tělesa \(\varepsilon_{ll}\) v sobě zahrnuje nejen vliv teploty podle (57), ale také vliv vnějšího zatížení. Objemová změna se dá v tomto obecném případě vyjádřit z entropie. V případě adiabatického zatěžování je entropie \(S\) konstantní. Entropie se dostane derivováním (54) podle teploty, tedy,

(60)\[\frac{\partial F}{\partial T}=S_0(T)+K\alpha\varepsilon_{ll}=S(T)=konst.\]

Entropie \(S\) a \(S_0\) nezávisí na teplotě \(T\) a jejich rozdíl je záporná tepelná kapacita za konstantního tlaku \(-C_p\). Z předchozího vztahu pak můžeme dostat objemovou změnu následovně,

(61)\[K_{ad}\alpha\varepsilon_{ll}=-C_p\quad\Rightarrow\quad\varepsilon_{ll}=-\frac{C_p}{K_{ad}\alpha},\]

kde \(K_{ad}\) je opět objemový modul \(K\) avšak při adiabatické deformaci. Dosazení (61) do (59) vede na vztah vyjadřující vztah mezi izotermickým a adiabatickým objemovým modulem,

(62)\[K_{ad}=K\bigg[1+\frac{K_{ad}\alpha^2\big(T-T_0\big)}{C_p}\bigg]\quad\Rightarrow\quad K=\frac{C_pK_{ad}}{C_p+K_{ad}\alpha^2\big(T-T_0\big)}.\]

V dalším se však bude předpokládat, že rozdíl mezi \(K\) a \(K_{ad}\) je minimální a nebudou se rozlišovat. To stejné budeme předpokládat u všech ostatních elastických konstant, tj. \(E\), \(\mu\) a \(\nu\).

V případě oblíbenosti ruského jazyka lze tohle všechno nalézt v krásné knize [1], existuje samozřejmě i anglické vydání.

Vztah mezi objemovou a délkovou roztažností

U vztahu (57) jsme nahraný, protože součet diagonálních složek tenzoru deformace nedává informaci o tom, jak mezi ně teplotní deformace rozložit. Cestou může být přibližné vyjádření objemové teplotní \(\alpha\) roztažnosti pomocí délkových teplotních roztažností ve směru hlavních os deformace. Protože řešíme případ izotropního materiálu, je jeho teplotní roztažnost \(\alpha_T\) ve všech směrech stejná a změna elementárního objemu se může vyjádřit následovně,

(63)\[\begin{split}\begin{equation} \begin{split} \varepsilon_{ll}=& \frac{\mathrm{d}V-\mathrm{dV_0}}{\mathrm{d}V_0} =\frac{\mathrm{d}l^3-\mathrm{d}l_0^3}{\mathrm{d}l_0^3} =\frac{\mathrm{d}l_0^3\big[1+\alpha_T\big(T-T_0\big)\big]^3-\mathrm{d}l_0^3}{\mathrm{d}l_0^3} \\ =& 3\alpha_T\big(T-T_0\big)+3\alpha_T^2\big(T-T_0\big)^2+\alpha_T^3\big(T-T_0\big)^3. \end{split} \end{equation}\end{split}\]

Protože je teplotní roztažnost malá, její vyšší mocniny se v předchozím vztahu zanedbají a z rovnosti

(64)\[\varepsilon_{ll}=\alpha\big(T-T_0\big)\approx3\alpha_T\big(T-T_0\big)\]

plyne, že

(65)\[\alpha_T=\frac{1}{3}\alpha.\]

Takže např. u prutové napjatosti i při teplotní deformaci pro tenzor napětí platí,

(66)\[\begin{split}T_\sigma=\left[\begin{array}{ccc} \sigma & \tau & 0\\ \tau & 0 & 0\\ 0 & 0 & 0 \end{array}\right],\end{split}\]

ale k tenzoru deformace se musí přidat přírůstek od teploty,

(67)\[\begin{split}T_\varepsilon=\left[\begin{array}{ccc} \varepsilon_x+\alpha_T\big(T-T_0\big) & \frac{\gamma_{xy}}{2} & 0\\ \frac{\gamma_{xy}}{2} & -\nu\varepsilon_x+\alpha_T\big(T-T_0\big) & 0\\ 0 & 0 & -\nu\varepsilon_x+\alpha_T\big(T-T_0\big) \end{array}\right].\end{split}\]

Podobně u válcového tělesa, teplota \(T\) tenzor napětí \(T_\sigma\) neovlivní,

(68)\[\begin{split}T_\sigma=\left[\begin{array}{ccc} \sigma_r & 0 & 0\\ 0 & \sigma_t & 0\\ 0 & 0 & \sigma_z \end{array}\right],\end{split}\]

kde

(69)\[\sigma_r=A-\frac{B}{r^2},\,\sigma_t=A+\frac{B}{r^2}\quad\mathrm{a} \quad\sigma_z=2\nu A+\frac{E(1-\nu)}{(1+\nu)(1-2\nu)}\varepsilon_z=p_z.\]

Konstanty \(A\), \(B\) a \(p_z\) se samozřejmě určí z okrajových podmínek. Vliv teploty se však projeví v dodatečném členu u diagonálních prvků tenzoru deformace,

(70)\[\begin{split}T_\varepsilon=\left[\begin{array}{ccc} \frac{\partial u}{\partial r}+\alpha_T\big(T-T_0\big) & 0 & 0\\ 0 & \frac{u}{r}+\alpha_T\big(T-T_0\big) & 0\\ 0 & 0 & \frac{\partial w}{\partial z}+\alpha_T\big(T-T_0\big) \end{array}\right],\end{split}\]

kde

(71)\[\begin{split}\begin{equation} \begin{split} u(r) =& \frac{(1+\nu)(1-2\nu)}{E}Ar+\frac{1+\nu}{E}\frac{B}{r},\\ \frac{\partial w}{\partial z}=\varepsilon_z =& \bigg(\frac{1}{9K}-\frac{1}{6\mu}\bigg) \big(\sigma_r+\sigma_t+\sigma_z\big)+\frac{1}{2\mu}\sigma_z. \end{split} \end{equation}\end{split}\]

Vztahy pro \(\sigma_z\) a \(\varepsilon_z\) se určí podle charakteru úlohy, viz http://www.old.utm.fme.vutbr.cz/~tprofant/pp2_vzorce.html

Literatura

[1]

Landau, L. D., Lifšic, E. M., Těorija uprugosti, Nauka, 1965, Moskva.

Smyková napětí v příčném průřezu kruhového tvaru

Základem je Žuravského vztah

(72)\[\tau_{xz}=\frac{TS_1\overline{z}_1}{YJ_y}=\frac{T\int_z^\frac{d}{2}z_1\mathrm{d}S_1}{YJ_y},\]

kde \(S_1\) je plocha úseče průřezu vymezená souřadnicí \(z\), \(\overline{z}_1\) je poloha těžiště této úseče, \(Y\) je šířka úseče a \(J_y\) je kvadratický moment průřezu. Pro šířku úseče vymezenou souřadnicí \(z_1\) platí,

(73)\[\bigg(\frac{Y_1}{2}\bigg)^2+z_1^2=\bigg(\frac{d}{2}\bigg)^2\]

a tedy

(74)\[Y_1=2\sqrt{\bigg(\frac{d}{2}\bigg)^2-z_1^2}.\]

Odtud se dostane pro diferenciál plochy \(\mathrm{d}S_1\) vztah

(75)\[\mathrm{d}S_1=Y_1\mathrm{d}z_1=2\mathrm{d}z_1\sqrt{\bigg(\frac{d}{2}\bigg)^2-z_1^2}.\]

A odtud z Žuravského vzorce plyne,

(76)\[\tau_{xz}=\frac{T\int_z^{\frac{d}{2}}2z_1\sqrt{\bigg(\frac{d}{2}\bigg)^2 -z_1^2}\mathrm{d}z_1}{2\sqrt{\bigg(\frac{d}{2}\bigg)^2-z^2}J_y} =\frac{\frac{2}{3}T\bigg[\bigg(\frac{d}{2}\bigg)^2-z^2\bigg] \sqrt{\bigg(\frac{d}{2}\bigg)^2-z^2}}{2\sqrt{\bigg(\frac{d}{2}\bigg)^2-z^2}J_y}.\]

Takže

(77)\[\tau_{xz}=\frac{T}{3J_y}\bigg[\bigg(\frac{d}{2}\bigg)^2-z^2\bigg].\]

Dále v případě \(z=0\), kde je \(\tau_{xz}\) maximální, se dostane

(78)\[\tau_{xz,max}=\frac{4T}{3S}.\]

Základní vztahy pružnosti a pevnosti II

Válcové těleso

Základní vztahy,

(79)\[\begin{split}\begin{equation} \begin{split} \sigma_r &= A-\frac{B}{r^2},\ \sigma_t = A+\frac{B}{r^2}, \\ \sigma_z &= 2\nu A+\left(2\mu+\lambda\right)\varepsilon_z =2\nu A+\frac{E\left(1-\nu\right)}{\left(1+\nu\right)\left(1-2\nu\right)}\varepsilon_z, \\ \varepsilon_r &= \frac{\partial u}{\partial r},\ \varepsilon_t = \frac{u}{r}, \ \varepsilon_z = \frac{\partial w}{\partial z}, \\ u &= \frac{\left(1+\nu\right)\left(1-2\nu\right)}{E}Ar+\frac{1+\nu}{E}\frac{B}{r}. \end{split} \end{equation}\end{split}\]

Okrajové podmínky \(\left.\sigma_r\right|_{r=r_1}=p_1\), \(\left.\sigma_r\right|_{r=r_2}=p_2\), \(\sigma_z=0\) - rovinná napjatost (např. tenký disk),

(80)\[\begin{split}\begin{equation} \begin{split} \sigma_r &= A-\frac{B}{r^2},\ \sigma_t = A+\frac{B}{r^2},\ \sigma_z = 0, \\ u &= \frac{\left(1+\nu\right)\left(1-2\nu\right)}{E}Ar+\frac{1+\nu}{E}\frac{B}{r}, \\ \varepsilon_r &= \frac{\partial u}{\partial r},\ \varepsilon_t = \frac{u}{r}, \ \varepsilon_z = -\frac{2\nu}{2\mu+\lambda}A. \end{split} \end{equation}\end{split}\]

Okrajové podmínky \(\left.\sigma_r\right|_{r=r_1}=p_1\), \(\left.\sigma_r\right|_{r=r_2}=p_2\), \(\varepsilon_z=0\) - rovinná deformace (např. hóóóódně dlouhá roura),

(81)\[\begin{split}\begin{equation} \begin{split} \sigma_r &= A-\frac{B}{r^2},\ \sigma_t = A+\frac{B}{r^2},\ \sigma_z = 2\nu A, \\ u &= \frac{\left(1+\nu\right)\left(1-2\nu\right)}{E}Ar+\frac{1+\nu}{E}\frac{B}{r}, \\ \varepsilon_r &= \frac{\partial u}{\partial r},\ \varepsilon_t = \frac{u}{r},\ \varepsilon_z = 0. \end{split} \end{equation}\end{split}\]

Okrajové podmínky \(\left.\sigma_r\right|_{r=r_1}=p_1\), \(\left.\sigma_r\right|_{r=r_2}=p_2\), \(\sigma_z=p_z\). K radiálnímu a tečnému napětí je nutné na základě superpozice a platnosti Hookeova zákona přidat přírůstek napětí, \(\sigma_r=\sigma_t=\lambda\varepsilon_z\), a deformace \(\varepsilon_z\) se vyjádří jako

(82)\[\varepsilon_z=\frac{p_z-2\nu A}{2\mu+\lambda}.\]

Celkově

(83)\[\begin{split}\begin{equation} \begin{split} \sigma_r &= A-\frac{B}{r^2}+\lambda\varepsilon_z =A-\frac{B}{r^2}+\lambda\frac{p_{z}-2\nu A}{2\mu+\lambda} =A^{'}-\frac{B}{r^2}, \\ \sigma_t &= A+\frac{B}{r^2}+\lambda\varepsilon_z =A+\frac{B}{r^2}+\lambda\frac{p_z-2\nu A}{2\mu+\lambda}=A^{'}+\frac{B}{r^2}, \\ \sigma_z &= p_z, \\ u &= \left(\frac{1-\nu}{E}A^{'}-\frac{\nu}{E}p_z\right)r+\frac{1+\nu}{E}\frac{B}{r}, \\ \varepsilon_r &= \frac{\partial u}{\partial r},\ \varepsilon_t = \frac{u}{r}, \ \varepsilon_z = \frac{1}{E}p_z-\frac{2\nu}{E}A^{'}. \end{split} \end{equation}\end{split}\]

kde

(84)\[A^{'}=\frac{2\mu+\lambda-2\nu\lambda}{2\mu+\lambda}A+\frac{\lambda}{2\mu\lambda}p_z =\frac{\left(1+\nu\right)\left(1-2\nu\right)}{1-\nu}A+\frac{\nu}{1-\nu}p_z.\]

Okrajové podmínky \(\left.\sigma_r\right|_{r=r_1}=p_1\), \(\left.\sigma_r\right|_{r=r_2}=p_2\), \(w=\Delta l\). K radiálnímu a tečnému napětí je nutné na základě superpozice a platnosti Hookeova zákona přidat přírůstek napětí, \(\sigma_r=\sigma_t=\lambda\varepsilon_z\), a deformace \(\varepsilon_z\) se vyjádří jako

(85)\[\varepsilon_z=\frac{\Delta l}{l}.\]

Celkově

(86)\[\begin{split}\begin{equation} \begin{split} \sigma_r &= A-\frac{B}{r^2}+\lambda\varepsilon_z =A-\frac{B}{r^2}+\lambda\frac{\Delta l}{l}=A^{'}-\frac{B}{r^2}, \\ \sigma_t &= A+\frac{B}{r^2}+\lambda\varepsilon_z=A+\frac{B}{r^2}+\lambda\frac{\Delta l}{l} =A^{'}+\frac{B}{r^2}, \\ \sigma_z &= 2\nu A^{'}+\frac{E\left(1-\nu+2\nu^2\right)}{\left(1+\nu\right) \left(1-2\nu\right)}\frac{\Delta l}{l}, \\ u &= \left(\frac{\left(1+\nu\right)\left(1-2\nu\right)}{E}A^{'}-\nu\frac{\Delta l}{l}\right)r +\frac{1+\nu}{E}\frac{B}{r}, \\ \varepsilon_r &= \frac{\partial u}{\partial r},\ \varepsilon_t = \frac{u}{r}, \ \varepsilon_z = \frac{\Delta l}{l}. \end{split} \end{equation}\end{split}\]

kde

(87)\[A^{'}=A+\lambda\frac{\Delta l}{l}=A+\frac{E\nu}{\left(1+\nu\right)\left(1-2\nu\right)}\frac{\Delta l}{l}.\]

Rotující stěna

Stěna je válcové těleso u kterého je \(h\ll r\), kde \(h\) je šířka stěny a \(r\) je vnější poloměr. Základní vztahy (rovinná napjatost),

(88)\[\begin{split}\begin{equation} \begin{split} \sigma_r &= A-\frac{B}{r^2}-\frac{3+\nu}{8}\rho\omega^2r^2, \ \sigma_t = A+\frac{B}{r^2}-\frac{1+3\nu}{8}\rho\omega^2r^2,\ \sigma_z = 0, \\ \varepsilon_r &= \frac{\partial u}{\partial r},\ \varepsilon_t = \frac{u}{r}, \ \varepsilon_z = -\frac{\nu}{E}\left[2A-\frac{1+\nu}{2}\rho\omega^2r^2\right], \\ u &= \frac{1-\nu}{E}Ar+\frac{1+\nu}{E}\frac{B}{r}-\frac{1-\nu^2}{8E}\rho\omega^2r^3, \end{split} \end{equation}\end{split}\]

kde \(\rho\) je hustota materiálu stěny a \(\omega\) je její úhlová rychlost.

Kruhová deska

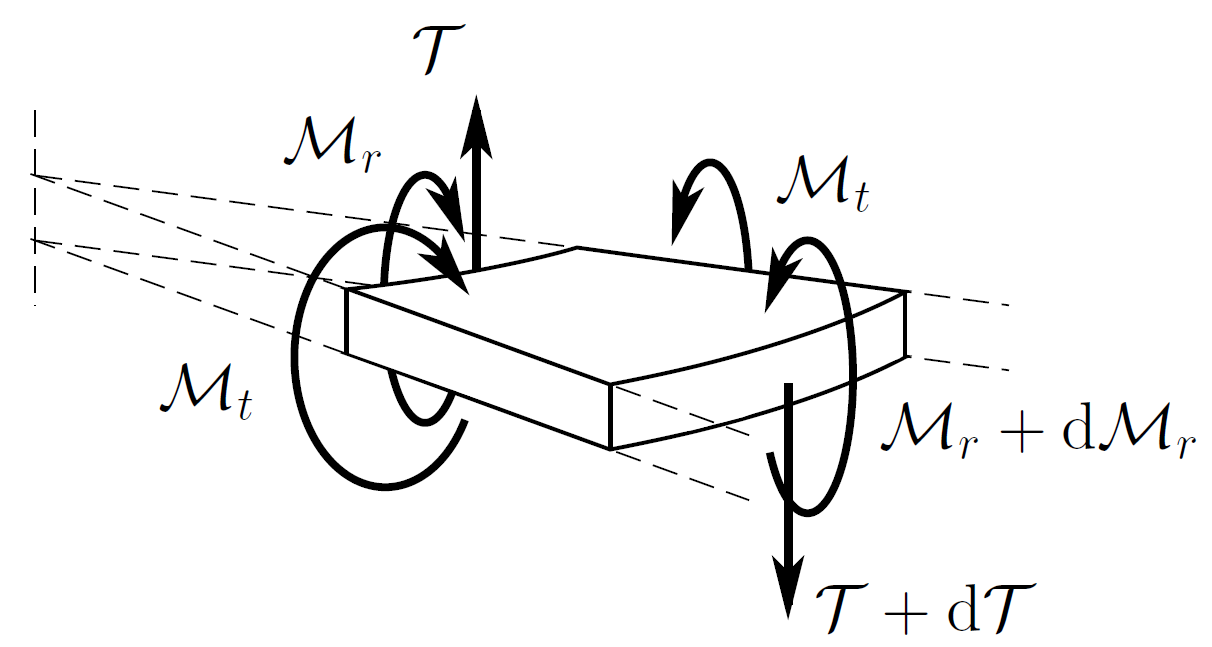
Uvolněný element kruhové desky.

Význam jednotlivých složek momentů a posouvajících sil je na obrázku výše. Základní vztahy pro kruhovou desku jsou

(89)\[\begin{split}\begin{equation} \begin{split} \vartheta &= C_1r+\frac{C_2}{r}+\vartheta_p, \ \vartheta_p = -\frac{1}{rB}\int\left[r\int\mathcal{T}\mathrm{d}r\right]\mathrm{d}r, \\ \mathcal{M}_r &= -B\left(\frac{\partial\vartheta}{\partial r}+\nu\frac{\vartheta}{r}\right), \ \mathcal{M}_t = -B\left(\frac{\vartheta}{r}+\nu\frac{\partial\vartheta}{\partial r}\right), \\ w &= \int\vartheta\mathrm{d}r+C_3, \\ \sigma_{r,\mathrm{ex}} &= \pm\frac{6\mathcal{M}_{r}}{h^{2}}, \ \sigma_{t,\mathrm{ex}} = \pm\frac{6\mathcal{M}_{t}}{h^{2}}, \end{split} \end{equation}\end{split}\]

kde \(h\) je tloušťka desky a

(90)\[B=\frac{Eh^3}{12\left(1-\nu^2\right)}\]

je tuhost desky.

Dlouhá válcová momentová skořepina

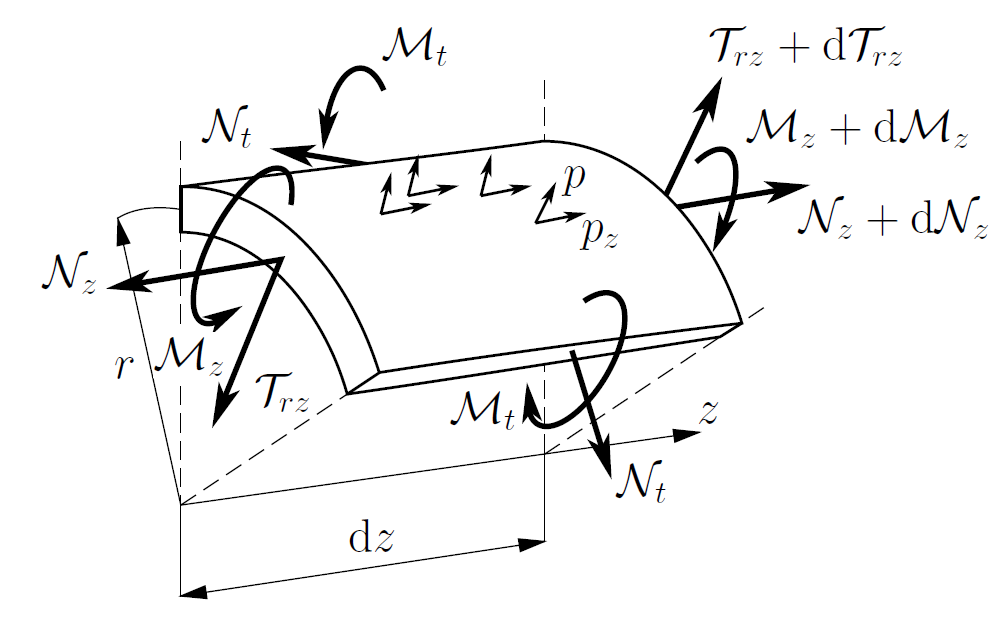
Uvolněný element válcové momentové skořepiny.

Význam jednotlivých složek výsledných momentů, sil a vnějšího zatížení působící na element skořepiny je na obrázku výše. Obecné řešení pro válcovou momentovou skořepinu má tvar

(91)\[u=\tilde{u}+u_p,\]

kde \(\tilde{u}\) je homogenní řešení

(92)\[\tilde{u}=\mathrm{e}^{-\beta z}\left(C_1\sin\beta z+C_2\cos\beta z\right)\]

a \(u_p\) je partikulární řešení

(93)\[u_p=\frac{r^2}{Eh}\left[p-\frac{\nu}{r}\left(C_0-\int p_z\mathrm{d}z\right)\right],\]

kde \(r\) je poloměr skořepiny a \(p\) a \(p_z\) jsou polynomy maximálně třetího stupně a

(94)\[\beta=\sqrt[4]{\frac{3\left(1-\nu^2\right)}{r^2h^2}}.\]

Další vztahy,

(95)\[\begin{split}\begin{equation} \begin{split} \vartheta =& \frac{\mathrm{d}u}{\mathrm{d}z} \\ =& -\beta\mathrm{e}^{-\beta z}\left[C_1\left(\sin\beta z-\cos\beta z\right) +C_2\left(\sin\beta z+\cos\beta z\right)\right]+\frac{\mathrm{d}}{\mathrm{d}z}u_p, \\ \mathcal{M}_z =& -B\frac{\mathrm{d}^2u}{\mathrm{d}z^2} \\ =& -2B\beta^2\mathrm{e}^{-\beta z}\left(-C_1\cos\beta z+C_2\sin\beta z\right) -B\frac{\mathrm{d}^2}{\mathrm{d}z^2}u_p, \\ \mathcal{M}_t =& \nu\mathcal{M}_r, \\ \mathcal{T}_{rz} =& \frac{\mathrm{d}\mathcal{M}_z}{\mathrm{d}z} \\ =& -2B\beta^3\mathrm{e}^{-\beta z}\left[C_1\left(\sin\beta z+\cos\beta z\right) +C_2\left(-\sin\beta z+\cos\beta z\right)\right] \\ &-B\frac{\mathrm{d}^3}{\mathrm{d}z^3}u_p, \end{split} \end{equation}\end{split}\]

kde

(96)\[B=\frac{Eh^3}{12\left(1-\nu^2\right)}\]

je tuhost skořepiny a \(h\) je tloušťka její stěny. Pro posuv \(w\) a sílu \(\mathcal{N}_z\) v axiálním směru a tangenciální sílu \(\mathcal{N}_t\) platí

(97)\[\begin{split}\begin{equation} \begin{split} w &= \frac{1-\nu^2}{E}\int\frac{\mathcal{N}_z}{h}\mathrm{d}z-\frac{\nu}{r}\int u\mathrm{d}z, \\ \mathcal{N}_z &= C_0-\int p_z\mathrm{d}z, \\ \mathcal{N}_t &= r\left(p_r+\frac{\mathrm{d}\mathcal{T}_{rz}}{\mathrm{d}z}\right). \end{split} \end{equation}\end{split}\]

Konečně pro extrémní hodnoty složek tenzoru napětí \(\sigma_z\) a \(\sigma_t\) platí,

(98)\[\begin{split}\begin{equation} \begin{split} \sigma_{z,\mathrm{ex}} &= \frac{\mathcal{N}_z}{h}\pm\frac{6\mathcal{M}_z}{h^2}, \\ \sigma_{t,\mathrm{ex}} &= \frac{\mathcal{N}_t}{h}\pm\frac{6\mathcal{M}_t}{h^2}. \end{split} \end{equation}\end{split}\]

Bezmomentová rotační skořepina

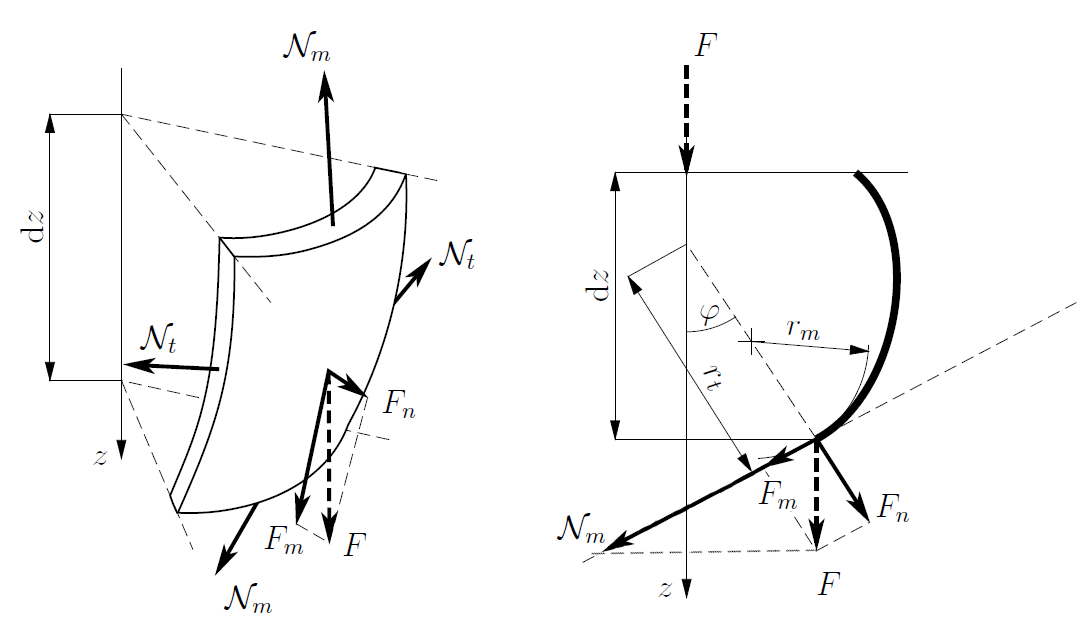
Uvolněný element rotační bezmomentové skořepiny.

Význam jednotlivých složek výsledných sil a vnějšího zatížení působící na element skořepiny je na obrázku výše. Pro rovnováhu na kružnici o poloměru \(r\) v bodě \(z\) a směru osy \(z\) platí,

(99)\[2\pi r\mathcal{N}_m\sin\varphi+F=0.\]

Na téže kružnici ve směru osy \(n\) platí,

(100)\[\frac{\mathcal{N}_m}{r_m}+\frac{\mathcal{N}_t}{r_t}=\frac{F_n}{S}.\]