Piezoelektricita - trhlina na rozhraní dvou piezoelektrických materiálů

Anizotropie materiálu se může rozšířit o piezoelektrické vlastnosti. U piezoelektrických materiálů se kromě napětí \(\boldsymbol{\sigma}\), deformace \(\boldsymbol{\varepsilon}\) a posuvů \(\boldsymbol{u}\) musí počítat s elektrickými posuvy \(\boldsymbol{D}\), elektrickým polem \(\boldsymbol{E}\) a elektrickým potenciálem \(\varphi\).

První dvě výše zmíněné veličiny \(\boldsymbol{\sigma}\) a \(\boldsymbol{\varepsilon}\) z klasické pružnosti mají tenzorový charakter a jsou navzájem svázány Hookeovým zákonem,

(1)\[\boldsymbol{\sigma}=\boldsymbol{C}\boldsymbol{\varepsilon},\]

kde

(2)\[\boldsymbol{\varepsilon}=\frac{1}{2}(\nabla\boldsymbol{u}+\boldsymbol{u}\nabla).\]

Piezoelektrické materiály jsou často ortotropní, takže při použití Voigtovy notace

(3)\[\begin{split}\boldsymbol{\sigma}=\left[\begin{array}{l} \sigma_{11} \\ \sigma_{22} \\ \sigma_{12} \end{array}\right], \qquad \boldsymbol{\varepsilon}=\left[\begin{array}{l} \varepsilon_{11} \\ \varepsilon_{22} \\ 2\varepsilon_{12} \end{array}\right]\end{split}\]

pro matici tuhosti \(\boldsymbol{C}\) platí

(4)\[\begin{split}\boldsymbol{C}=\boldsymbol{S}^{-1}=\left[\begin{array}{lll} 1/E_L & -\nu_{LT}/E_L & 0 \\ -\nu_{LT}/E_L & 1/E_T & 0 \\ 0 & 0 & 1/G_{LT} \end{array}\right]^{-1}.\end{split}\]

V elektrostatice je elektrická indukce \(\boldsymbol{D}\) a elektrické pole \(\boldsymbol{E}\) pouze vektor, ale jsou také lineárně navzájem svázány (jako tenzor napětí \(\boldsymbol{\sigma}\) a deforamce \(\boldsymbol{\varepsilon}\))

(5)\[\boldsymbol{D}=\boldsymbol{\omega}\boldsymbol{E},\]

kde

(6)\[\begin{split}\boldsymbol{D}=\left[\begin{array}{l} D_1 \\ D_2 \end{array}\right],\qquad \boldsymbol{E}=\left[\begin{array}{l} E_1 \\ E_2 \end{array}\right],\end{split}\]

(7)\[\begin{split}\boldsymbol{\omega}=\left[\begin{array}{ll} \omega_{11} & 0 \\ 0 & \omega_{22} \end{array}\right]\end{split}\]

je matice permitivity dialektrika pro případ ortotropního materiálu elektricky polarizovaného ve směru osy \(x_1\). Pro elektrické pole \(\boldsymbol{E}\) platí

(8)\[\boldsymbol{E}=-\nabla\varphi.\]

Piezoelektricita je spojením pružnosti s elektrostatikou skrz tzv. piezoelektrické koeficienty \(e_{ijk}\), kde se však místo indukce zavádí tzv. elektrické posuvy \(\boldsymbol{D}\). Hookeův zákon pro piezoelektrický materiál má při Voigtově notaci tvar

(9)\[\begin{split}\begin{equation} \begin{split} \boldsymbol{\sigma} =& \boldsymbol{C}\boldsymbol{\varepsilon}-\boldsymbol{e}^T\boldsymbol{E}, \\ \boldsymbol{D} =& \boldsymbol{e}\boldsymbol{\varepsilon}+\boldsymbol{\omega}\boldsymbol{E} \end{split} \end{equation}\end{split}\]

kde

(10)\[\begin{split}\boldsymbol{e}=\left[\begin{array}{lll} e_{11} & e_{12} & 0 \\ 0 & 0 & e_{26} \end{array}\right]\end{split}\]

je matice piezoelektrických koeficientů pro případ ortotropního materiálu a elektrické polarizace ve směru osy \(x_1\). Úloha se musí řešit jako "mixed value", kde se hledají současně dvě řešení, vektor posuvů \(\boldsymbol{u}\) a skalár elektrického potenciálu \(\varphi\). Slabá formulace se tedy skládá ze dvou rovnic

(11)\[-\int_\Omega\boldsymbol{\sigma}:\delta\boldsymbol{\varepsilon}\mathrm{d}\Omega +\int_\Omega\boldsymbol{D}\cdot\delta\boldsymbol{E}\mathrm{d}\Omega +\int_{\partial\Omega}\boldsymbol{t}\cdot\delta\boldsymbol{u}\mathrm{d}\partial\Omega -\int_{\partial\Omega}q\delta\varphi\mathrm{d}\partial\Omega=0,\]

kde

(12)\[\boldsymbol{t}=\boldsymbol{\sigma}\cdot\boldsymbol{n}\]

je vektor napětí a

(13)\[q=\frac{1}{4\pi}\nabla\cdot\boldsymbol{E}\]

je elektrický náboj na povrchu. Dirichletovy podmínky mají tvar

(14)\[\boldsymbol{u}=\overline{\boldsymbol{u}}, \ \varphi=\overline{\varphi}\quad\mathrm{na}\ \partial\Omega.\]

Formulace úlohy

Uvažujme dvourozměrnou oblast \(\Omega\) složenou za dvou piezoelektrických materiálů. Rozhraní obou materiálů leží podél osy \(x\), přičemž podél její záporné části se nachází trhlina. Geometrie, uložení, vnější zatížení a poloha vzhledem k počátku souřadnicového systému jsou na následujícím obrázku.

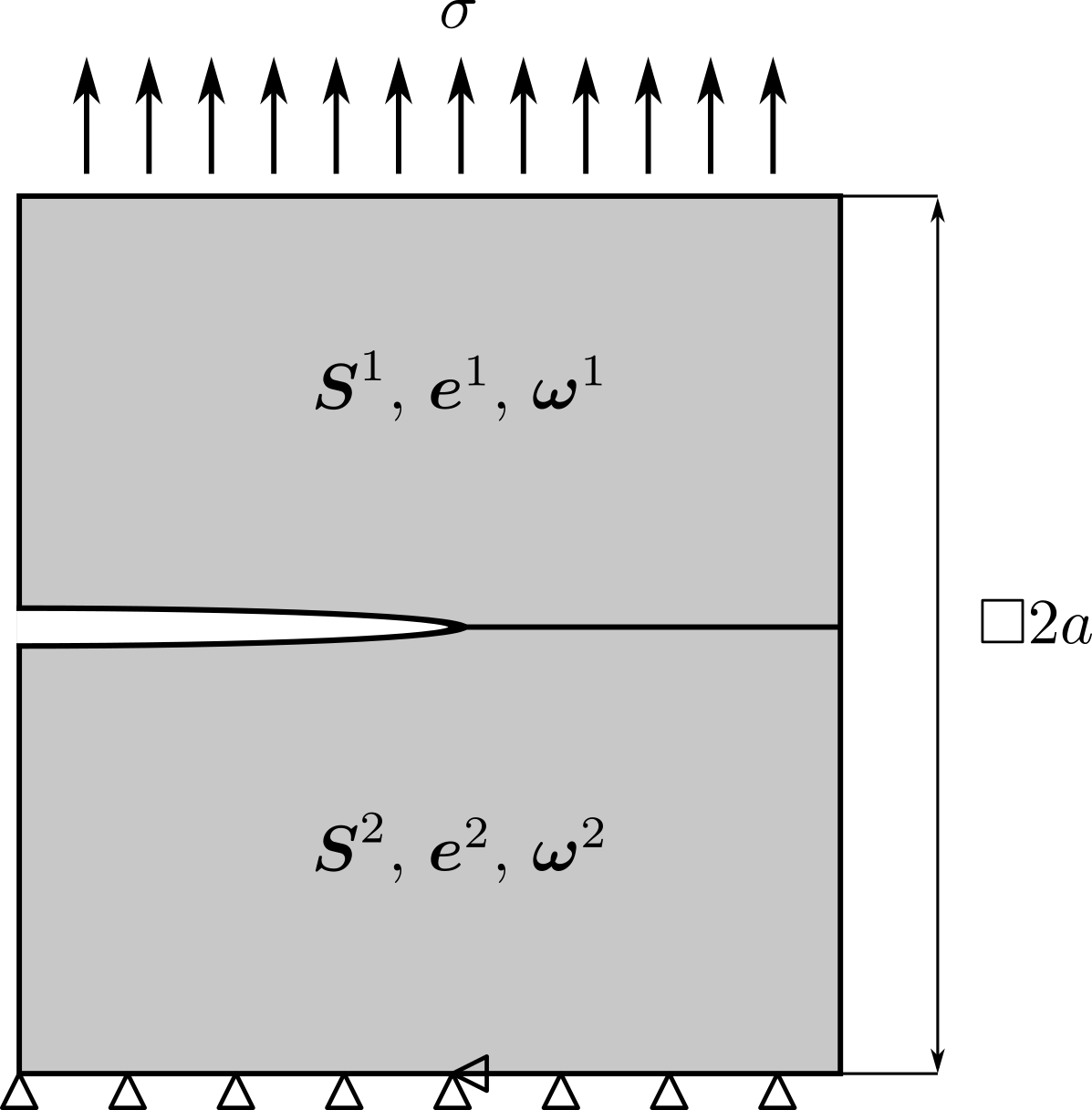
Rozměry a zatížení tělesa jsou následující

(15)\[\sigma=10^4\,\mathrm{Pa},\qquad a=90\times 10^{-3}\,\mathrm{m}.\]

Eelastické i piezoelektrické konstanty uvažovaných materiálů obsahují tyto tabulky

materiál	PZT-5H	PZT-4
\(C_{11}\)	\(11.7\times 10^{10}\,\mathrm{Pa}\)	\(11.3\times 10^{10}\,\mathrm{Pa}\)
\(C_{12}\)	\(5.30\times 10^{10}\,\mathrm{Pa}\)	\(7.43\times 10^{10}\,\mathrm{Pa}\)
\(C_{23}\)	\(5.50\times 10^{10}\,\mathrm{Pa}\)	\(7.78\times 10^{10}\,\mathrm{Pa}\)
\(C_{22}\)	\(12.6\times 10^{10}\,\mathrm{Pa}\)	\(13.9\times 10^{10}\,\mathrm{Pa}\)
\(C_{44}\)	\(3.53\times 10^{10}\,\mathrm{Pa}\)	\(2.56\times 10^{10}\,\mathrm{Pa}\)
\(C_{66}\)	\(\big(C_{22}-C_{23}\big)/2\)	\(\big(C_{22}-C_{23}\big)/2\)
\(e_{12}\)	\(-6.50\,\mathrm{C/m^2}\)	\(-6.98\,\mathrm{C/m^2}\)
\(e_{11}\)	\(23.30\,\mathrm{C/m^2}\)	\(13.84\,\mathrm{C/m^2}\)
\(e_{26}\)	\(17.00\,\mathrm{C/m^2}\)	\(13.44\,\mathrm{C/m^2}\)
\(\omega_{11}\)	\(13.0\times 10^{-9}\,\mathrm{C/Vm}\)	\(5.47\times 10^{-9}\,\mathrm{C/Vm}\)
\(\omega_{22}\)	\(15.1\times 10^{-9}\,\mathrm{C/Vm}\)	\(6.00\times 10^{-9}\,\mathrm{C/Vm}\)

materiál	PZT-7A	BaTiO3
\(C_{11}\)	\(13.1\times 10^{10}\,\mathrm{Pa}\)	\(14.6\times 10^{10}\,\mathrm{Pa}\)
\(C_{12}\)	\(7.42\times 10^{10}\,\mathrm{Pa}\)	\(6.60\times 10^{10}\,\mathrm{Pa}\)
\(C_{23}\)	\(7.62\times 10^{10}\,\mathrm{Pa}\)	\(6.60\times 10^{10}\,\mathrm{Pa}\)
\(C_{22}\)	\(14.8\times 10^{10}\,\mathrm{Pa}\)	\(15.0\times 10^{10}\,\mathrm{Pa}\)
\(C_{44}\)	\(2.54\times 10^{10}\,\mathrm{Pa}\)	\(4.40\times 10^{10}\,\mathrm{Pa}\)
\(C_{66}\)	\(\big(C_{22}-C_{23}\big)/2\)	\(\big(C_{22}-C_{23}\big)/2\)
\(e_{12}\)	\(-2.10\,\mathrm{C/m^2}\)	\(-4.35\,\mathrm{C/m^2}\)
\(e_{11}\)	\(9.50\,\mathrm{C/m^2}\)	\(17.50\,\mathrm{C/m^2}\)
\(e_{26}\)	\(9.70\,\mathrm{C/m^2}\)	\(11.40\,\mathrm{C/m^2}\)
\(\omega_{11}\)	\(7.35\times 10^{-9}\,\mathrm{C/Vm}\)	\(11.2\times 10^{-9}\,\mathrm{C/Vm}\)
\(\omega_{22}\)	\(8.11\times 10^{-9}\,\mathrm{C/Vm}\)	\(9.87\times 10^{-9}\,\mathrm{C/Vm}\)

Použité skripty

Skripty jsou platné pro FEniCS v2018.1.0.

• bicrack2_piezo.py - pythonovský skript pro FEniCS

• bicrack0_gmsh.py - pythonovský skript, který vytvoří a zkompiluje soubor bicrack0.geo a dále vytvoří konečnoprvkovou síť bicrack0.msh.

• ANSYS_mat1_raw_data_180_90.dat, ANSYS_mat2_raw_data_180_90.dat - data z ANSYSu.

• LES_Mirek0.py, mod_HSV_v4.py, mod_plot_fcn.py - pythonovský skript a nutné moduly počítající exponenty singularity napětí a součinitele intenzity napětí na čele trhliny.