Rovinný pohyb

V kinematice se převážně vyjadřují závislosti vektorů polohy \(\boldsymbol{r}\), rychlosti \(\boldsymbol{v}\) a zrychlení bodu \(\boldsymbol{a}\) v polárních souřadnicích \((r,\varphi)\). Parametr \(r\) reprezentuje vzdálenost bodu od počátku souřadnic a \(\varphi\) reprezentuje úhel, zpravidla odečítaný proti směru hodinových ručiček od vodorovné osy roviny. Pro případ obecného rovinného (nejen) pohybu je to totiž velmi praktické. Pro fajnšmekry jsou v následujícím textíku odvozeny fundamentální vztahy pro vektory \(\boldsymbol{r}\), \(\boldsymbol{v}\) a \(\boldsymbol{a}\) v polárních souřadnicích pro rovinný pohyb.

Základní vlastnosti bázových vektorů polárního souřadnicového systému

Předpokládáme funkční závislosti souřadnic

(1)\[r=r(t)\quad\mathrm{a}\quad\varphi=\varphi(t),\]

na parametru \(t\in\mathbb{R}\). Parametr \(t\) je reálný, většinou kladný a čas reprezentující. Veličiny \(r\in[0,\infty]\) a \(\varphi\in[0,2\pi]\) jsou polární souřadnice nějakého rádius vektoru bodu

(2)\[\boldsymbol{r}=\boldsymbol{r}(r,\varphi)=r\boldsymbol{e}_{r}+\varphi\boldsymbol{e}_{\varphi}.\]

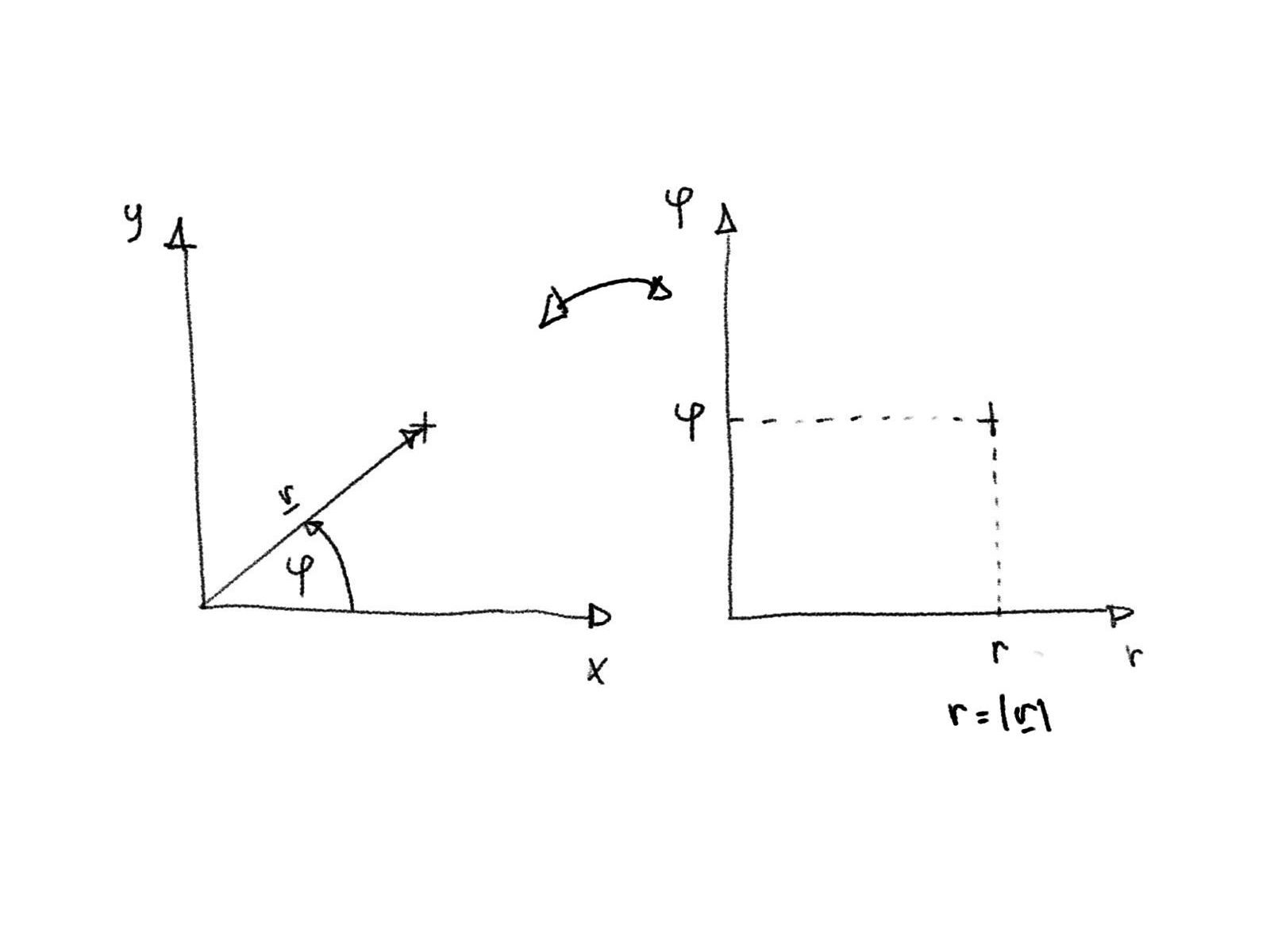
Obrázek: Zobrazení bodu v kartézském \((x,y)\) a polárním \((r,\varphi)\) souřadnicovém systému.

Jednotkové vektory \(\boldsymbol{e}_{r}\) a \(\boldsymbol{e}_{\varphi}\) jsou bázové vektory polárního souřadnicového systému \((r,\varphi)\), pro které platí

(3)\[\begin{split}\boldsymbol{e}_{r} &=(\cos\varphi,\sin\varphi), \\ \boldsymbol{e}_{\varphi} &=(-\sin\varphi,\cos\varphi).\end{split}\]

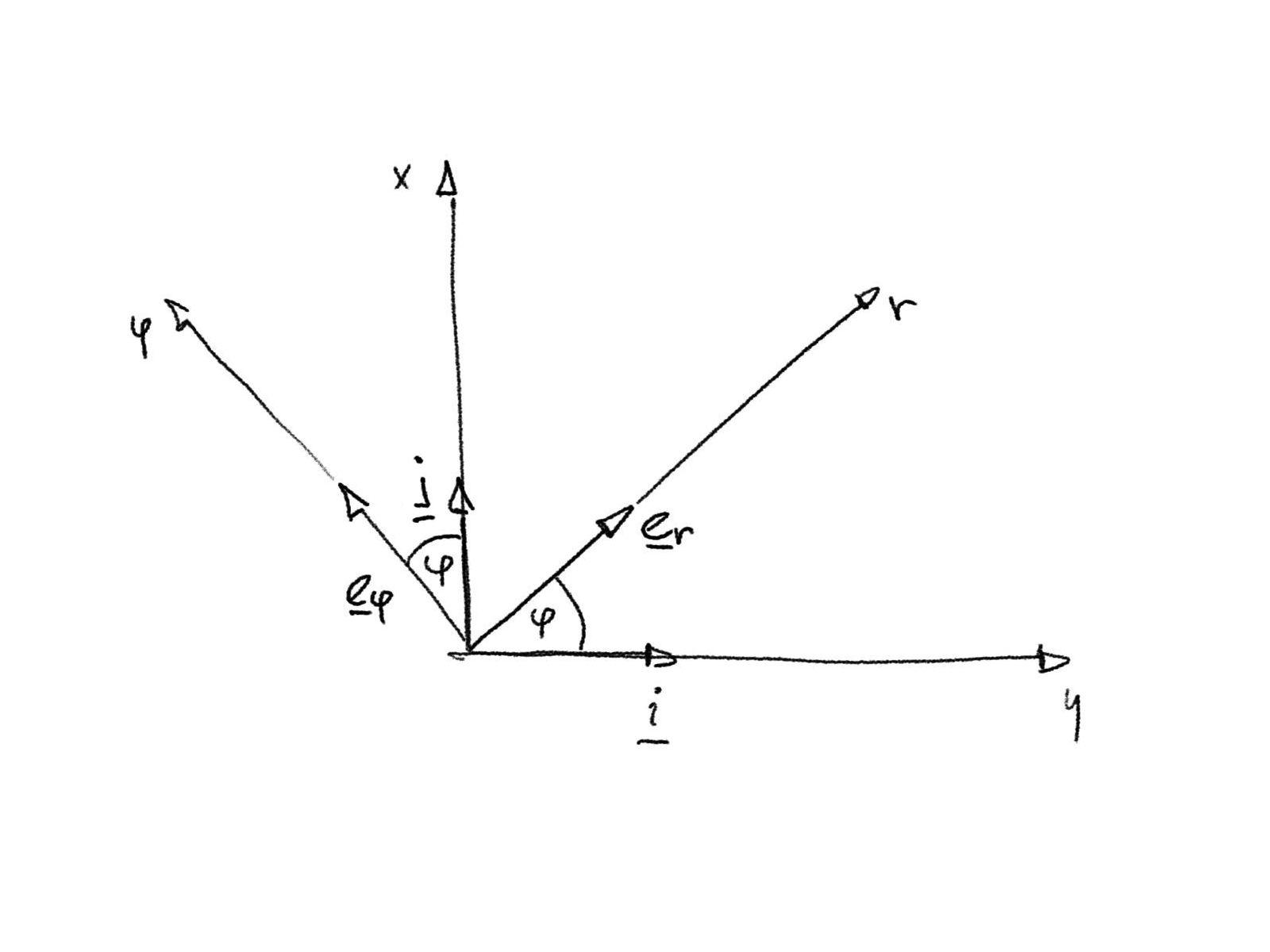
Obrázek: Bázové vektory \(\boldsymbol{e}_r\) a \(\boldsymbol{e}_\varphi\) polárního souřadnicového systému \((r,\varphi)\) a jejich vztah k bázovým vektorům \(\boldsymbol{i}\) a \(\boldsymbol{j}\) kartézského souřadnicového systému \((x,y)\).

Derivace podle parametru \(t\) souřadnic \(r\) a \(\varphi\) značíme v kinematice následovně

(4)\[\frac{\mathrm{d}}{\mathrm{d}t}r=\dot{r}=v, \quad\frac{\mathrm{d^{2}}}{\mathrm{d}t^{2}}r=\ddot{r}=\dot{v}=a,\]

(5)\[\frac{\mathrm{d}}{\mathrm{d}t}\varphi=\dot{\varphi}=\omega, \quad\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}\varphi=\ddot{\varphi}=\dot{\omega}=\alpha.\]

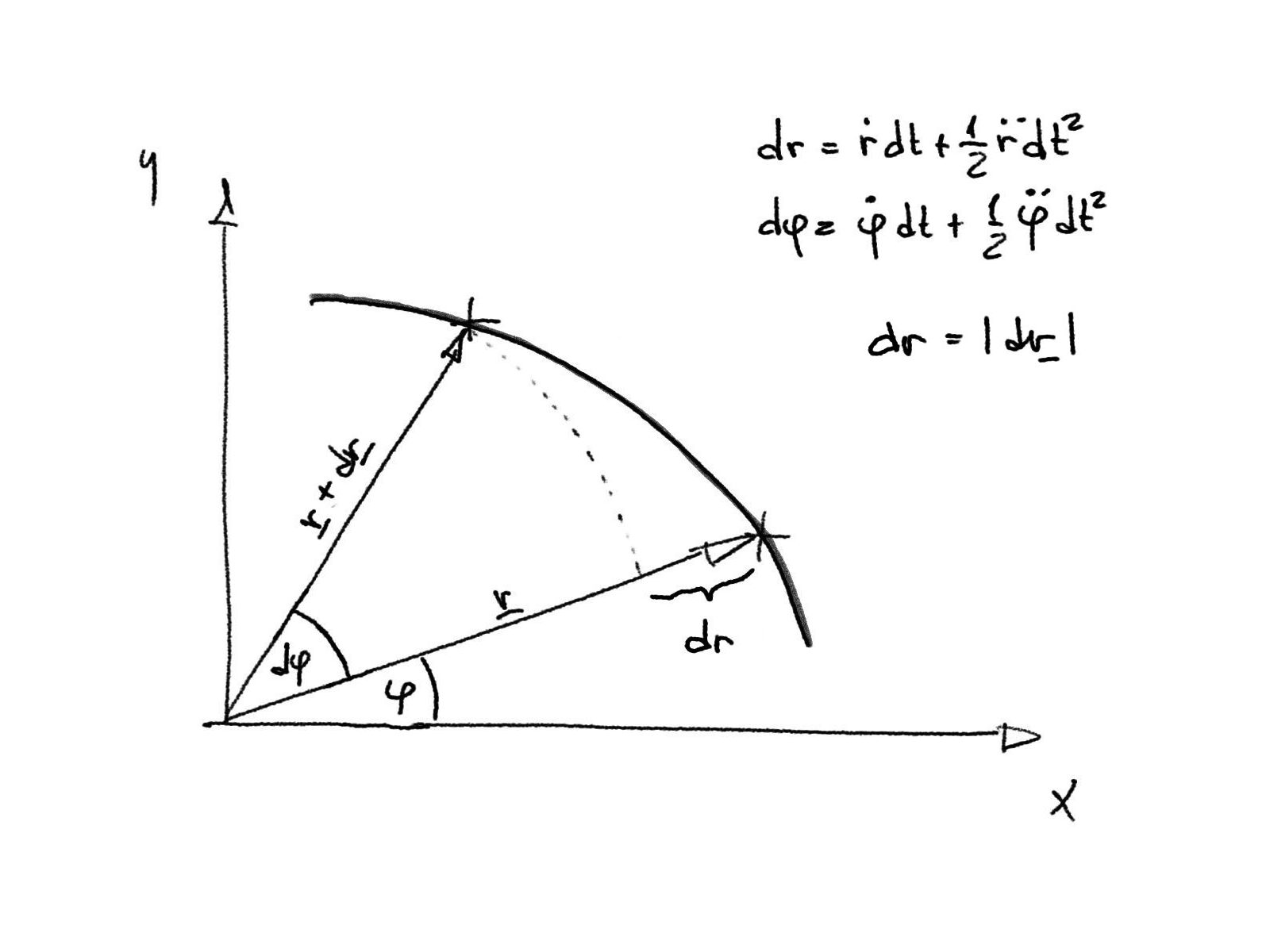
Obrázek: Geometrický význam derivace velikosti rádius vektoru \(|\boldsymbol{r}|\equiv r\) a úhlu \(\varphi\) podle parametru (času) \(t\).

Fyzikální význam \(v\) a \(a\) je rychlost a zrychlení přímočarého pohybu bodu a význam \(\omega\) a \(\alpha\) je úhlová rychlost a zrychlení při rotačním pohybu rádius vektoru bodu \(\boldsymbol{r}\). Pro derivace jednotkových vektorů \(\boldsymbol{e}_{r}\) a \(\boldsymbol{e}_{\varphi}\) podle parametru \(t\) platí

(6)\[\begin{split}\frac{\mathrm{d}}{\mathrm{d}t}\boldsymbol{e}_{r} &= \dot{\boldsymbol{e}}_{r} =\frac{\mathrm{d}}{\mathrm{d}\varphi}\boldsymbol{e}_{r}\dot{\varphi} =\boldsymbol{e}_{\varphi}\dot{\varphi} =\boldsymbol{e}_{\varphi}\omega, \\ \frac{\mathrm{d}}{\mathrm{d}t}\boldsymbol{e}_{\varphi} &= \dot{\boldsymbol{e}}_{\varphi} =\frac{\mathrm{d}}{\mathrm{d}\varphi}\boldsymbol{e}_{\varphi}\dot{\varphi} =-\boldsymbol{e}_{r}\dot{\varphi}=-\boldsymbol{e}_{r}\omega.\end{split}\]

Jednotkové vektory \(\boldsymbol{e}_{r}\) a \(\boldsymbol{e}_{\varphi}\) se nemohou zkracovat nebo prodlužovat, mohou se však (v čase \(t\)) natáčet, což právě tyto vztahy říkají.

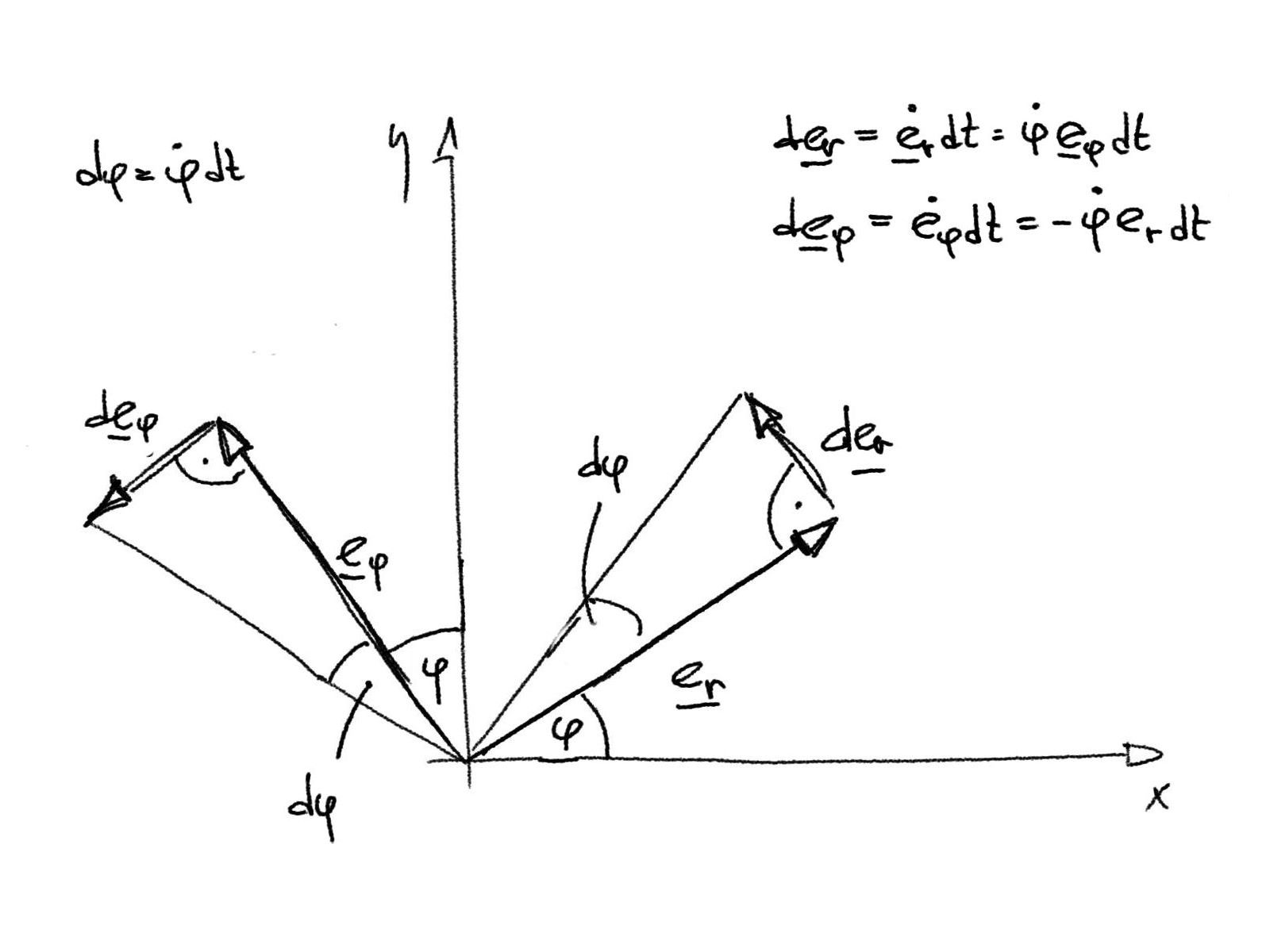
Obrázek: Geometrický význam derivace bázových vektorů \(\boldsymbol{e}_r\) a \(\boldsymbol{e}_\varphi\) polárního souřadnicového systému \((r,\varphi)\) podle parametru (času) \(t\).

Přímočarý pohyb

U přípmočarého pohybu se předpokládá, že se rádius vektor \(\boldsymbol{r}\) bodu v zafixovaném směru prodlužuje nebo zkracuje, tedy

(7)\[r=r(t)\quad\mathrm{a}\quad\varphi=\mathrm{konst.}\]

Takže

(8)\[\dot{\varphi}=0\]

a

(9)\[\dot{\boldsymbol{e}}_{r}=\dot{\boldsymbol{e}}_{\varphi}=0.\]

Rádius vektor \(\boldsymbol{r}\) bodu v polárních souřadnicích \((r,\varphi)\) se zpravila volí tak (není to nutné, ale velmi výhodné), že leží na ose \(r\) polárního souřadnicového systému, tj.

(10)\[\boldsymbol{r}=r\boldsymbol{e}_{r}.\]

Pak tedy pro vektor rychlosti \(\boldsymbol{v}\) a zrychlení \(\boldsymbol{a}\) bodu platí

(11)\[\begin{split}\boldsymbol{v} &= \dot{\boldsymbol{r}}=\dot{r}\boldsymbol{e}_{r}+r\dot{\boldsymbol{e}}_{r} =\dot{r}\boldsymbol{e}_{r}=v\boldsymbol{e}_{r}, \\ \boldsymbol{a} &= \dot{\boldsymbol{v}}=\ddot{r}\boldsymbol{e}_{r}+\dot{r}\dot{\boldsymbol{e}}_{r} =\ddot{r}\boldsymbol{e}_{r}=a\boldsymbol{e}_{r}.\end{split}\]

Význam \(v\) a \(a\) je, jak je uvedeno výše, rychlost a zrychlení přímočarého pohybu bodu.

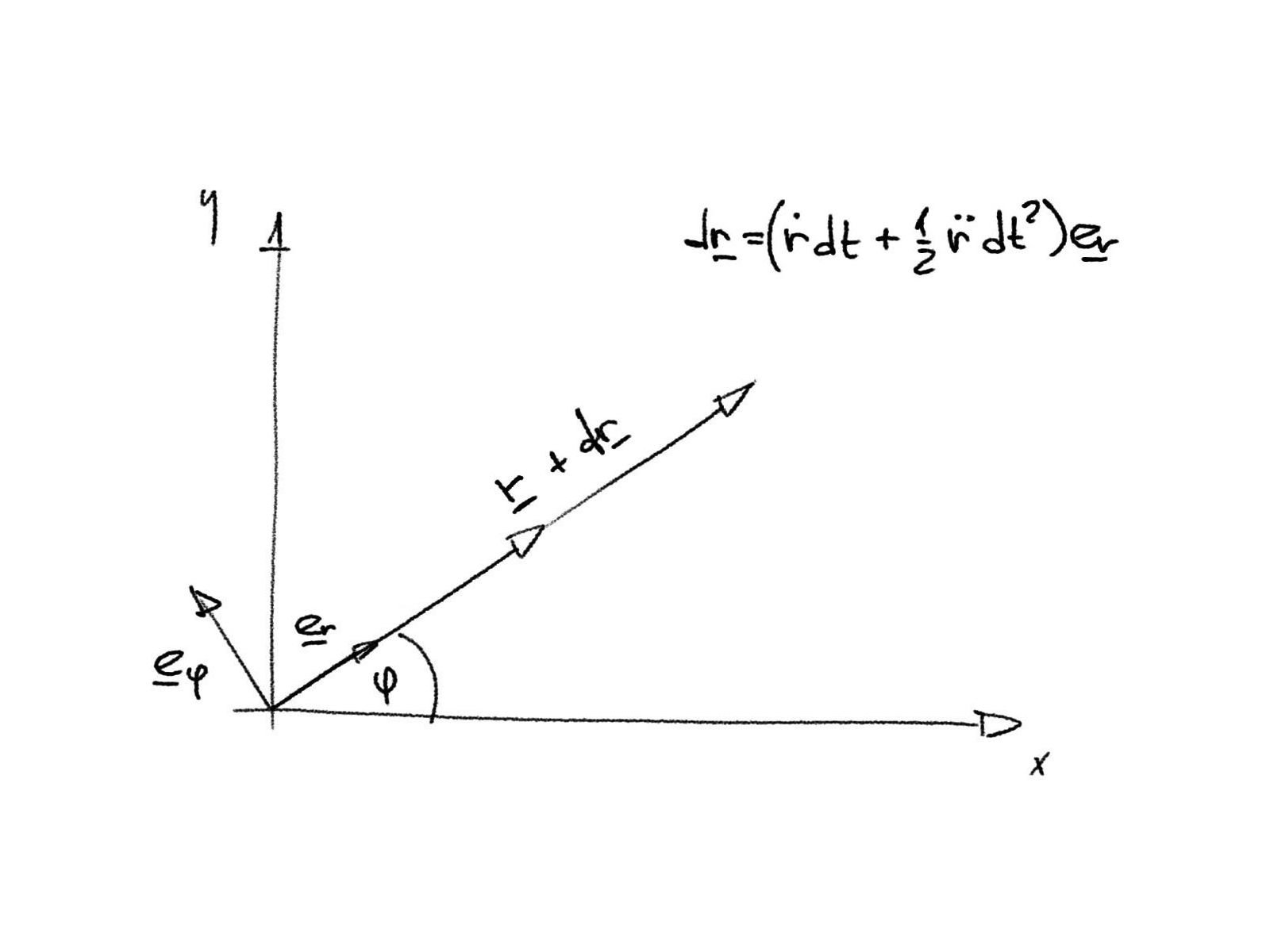
Obrázek: Geometrický význam jednotlivých přírůstků polohy bodu v polárním souřadnicovém systému \((r,\varphi)\) od rychlosti \(v=\dot{r}\) a zrychlení \(a=\ddot{r}\) při přímočarém pohybu.

Rotační pohyb

U rotačního pohybu předpokládáme, že se rádius vektor bodu \(\boldsymbol{r}\) neprodlužuje, ale rotuje kolem počátku souřadnic, tj.

(12)\[r=\mathrm{konst.}\quad\mathrm{a}\quad\varphi=\varphi(t).\]

Takže platí jediná podmínka

(13)\[\dot{r}=0.\]

Rádius vektor \(\boldsymbol{r}\) nějakého bodu v polárním souřadnicovém systému se i zde výhodně volí tak, že leží na ose \(r\) souřadnicového systému, tj.

(14)\[\boldsymbol{r}=r\boldsymbol{e}_{r}.\]

Pak platí

(15)\[\boldsymbol{v}=\dot{\boldsymbol{r}}=\dot{r}\boldsymbol{e}_{r}+r\dot{\boldsymbol{e}}_{r} =r\omega\boldsymbol{e}_{\varphi},\]

(16)\[\boldsymbol{a}=\dot{\boldsymbol{v}}=\dot{r}\omega\boldsymbol{e}_{\varphi} +r\dot{\omega}\boldsymbol{e}_{\varphi}+r\omega\dot{\boldsymbol{e}}_{\varphi} =r\alpha\boldsymbol{e}_{\varphi}-r\omega^{2}\boldsymbol{e}_{r}.\]

Vektor

(17)\[\boldsymbol{v}=r\omega\boldsymbol{e}_{\varphi}\]

je obvodová rychlost bodu a vektory

(18)\[\boldsymbol{a}_{t}=r\alpha\boldsymbol{e}_{\varphi}\quad\mathrm{a}\quad \boldsymbol{a}_{n}=-r\omega^{2}\boldsymbol{e}_{r}=-r\frac{v^{2}}{r^{2}}\boldsymbol{e}_{r} =-\frac{v^{2}}{r}\boldsymbol{e}_{r}\]

jsou tečné a normálové (dostředivé) zrychlením bodu.

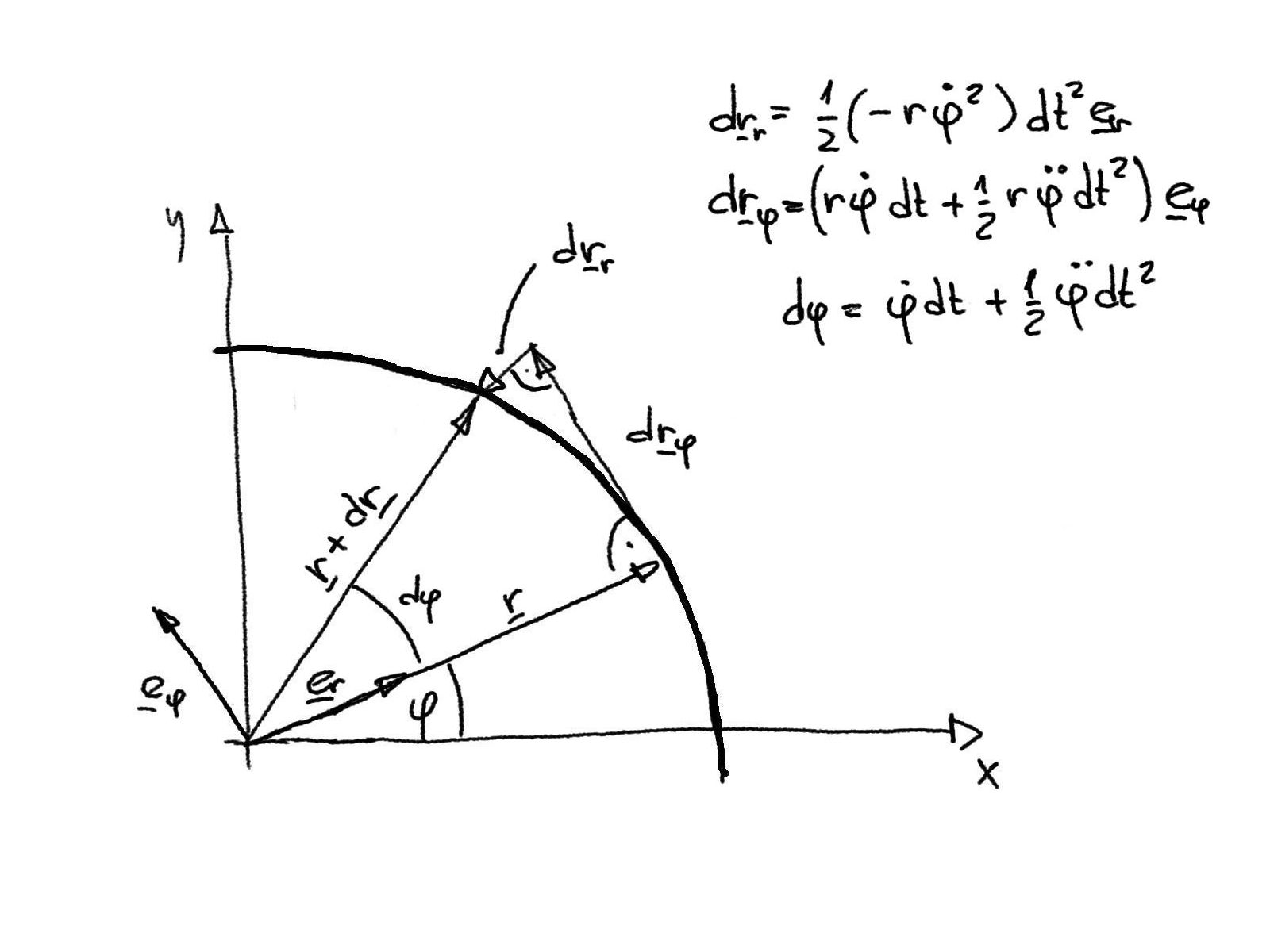
Obrázek: Geometrický význam jednotlivých přírůstků polohy bodu v polárním souřadnicovém systému \((r,\varphi)\) od rychlosti \(\dot{\varphi}r=\omega r\) a tečného zrychlení \(a_t=\ddot{\varphi}r=\alpha r\) a normálového zrychlení \(a_n=\dot{\varphi}^2r=\omega^2r\) při rotačním pohybu bodu.

Rovinný pohyb

V obecném případu rovinného pohybu se na rádius \(r\) a úhel \(\varphi\) nekladou žádné požadavky, tj.

(19)\[r=r(t)\quad\mathrm{a}\quad\varphi=\varphi(t)\]

a podobně jako v případě translačního a rotačního pohybu se rádius vektor bodu \(\boldsymbol{r}\) v polárních souřadnicích \((r,\varphi)\) zpravila volí tak, že

(20)\[\boldsymbol{r}=r\boldsymbol{e}_{r}.\]

Pak pro rychlost bodu \(\boldsymbol{v}\) platí

(21)\[\boldsymbol{v}=\dot{\boldsymbol{r}}=\dot{r}\boldsymbol{e}_{r}+r\dot{\boldsymbol{e}}_{r} =v\boldsymbol{e}_{r}+r\omega\boldsymbol{e}_{\varphi}.\]

To znamená, že vektor rychlosti \(\boldsymbol{v}\) je vektorovým součtem rychlosti translačního pohybu \(v\boldsymbol{e}_{r}\) a vektoru obvodové rychlosti \(r\omega\boldsymbol{e}_{\varphi}\). Pro zrychlení platí

(22)\[\begin{split}\boldsymbol{a}=\dot{\boldsymbol{v}} =& \ddot{r}\boldsymbol{e}_{r}+\dot{r}\dot{\boldsymbol{e}}_{r} +\dot{r}\omega\boldsymbol{e}_{\varphi} +r\dot{\omega}\boldsymbol{e}_{\varphi}+r\omega\dot{\boldsymbol{e}}_{\varphi} \\ =& a\boldsymbol{e}_{r}+\dot{r}\omega\boldsymbol{e}_{\varphi}+\dot{r}\omega\boldsymbol{e}_{\varphi} +r\dot{\omega}\boldsymbol{e}_{\varphi}-r\omega^{2}\boldsymbol{e}_{r} \\ =& (\ddot{r}-r\omega^{2})\boldsymbol{e}_{r}+(2\dot{r}\omega+r\alpha)\boldsymbol{e}_{\varphi} \\ =& (a-a_{n})\boldsymbol{e}_{r}+(2\dot{r}\omega+a_{t})\boldsymbol{e}_{\varphi}.\end{split}\]

Vektor zrychlení \(\boldsymbol{a}\) bodu, podobně jako vektor jeho rychlosti \(\boldsymbol{v}\), je kombinací vektorů zrychlení přímočarého pohybu, tečného zrychlení a dostředivého zrychlení \(a\boldsymbol{e}_{r}\), \(a_{t}\boldsymbol{e}_{\varphi}\) a \(a_{n}\boldsymbol{e}_{r}\). Navíc se zde objevuje vektor tzv. Coriolisova zrychlení

(23)\[\boldsymbol{a}_{c}=2\dot{r}\omega\boldsymbol{e}_{\varphi}.\]

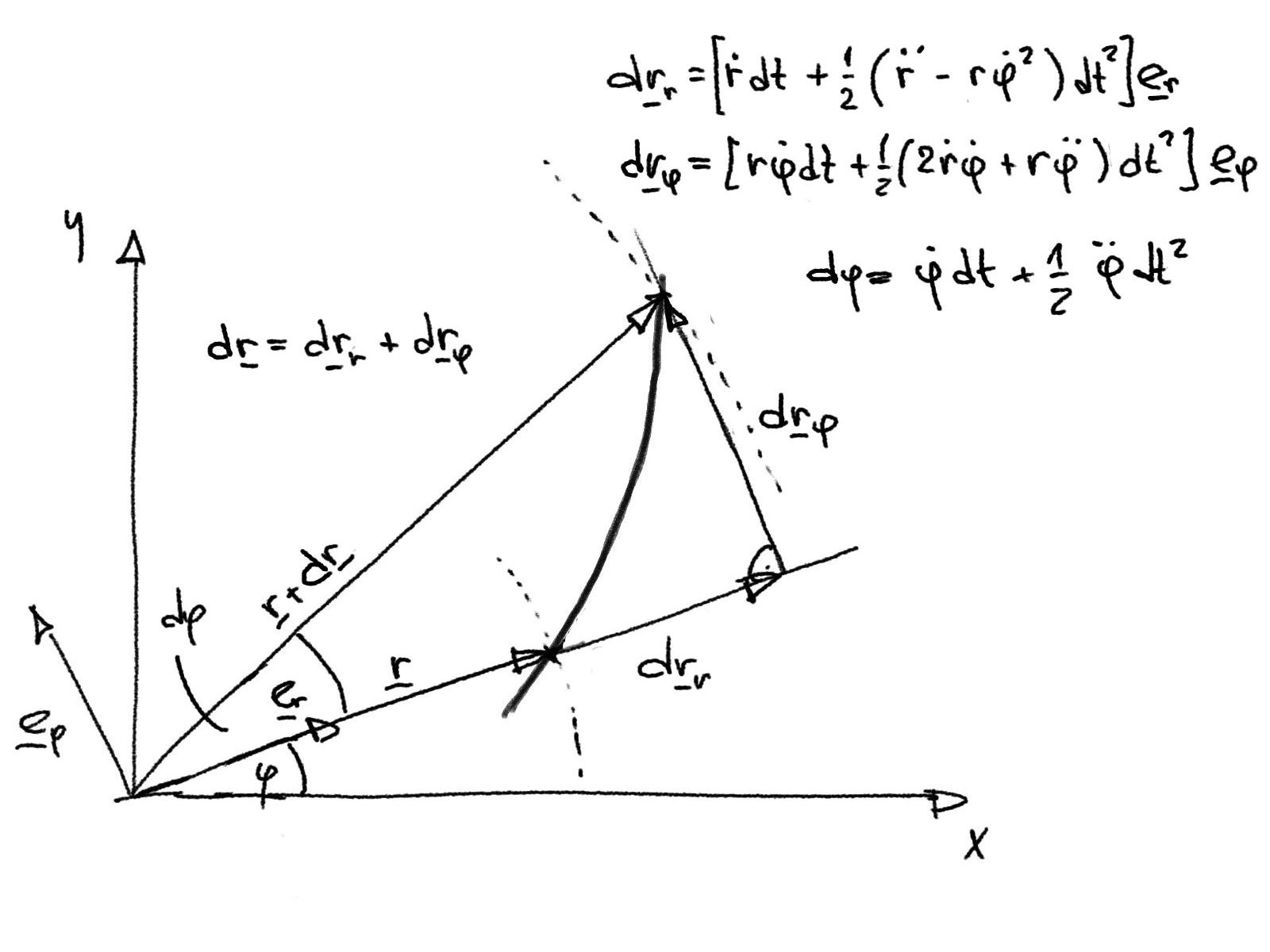
Obrázek: Geometrický význam jednotlivých přírůstků polohy bodu v polárním souřadnicovém systému \((r,\varphi)\) od rychlostí \(\dot{r}\) a \(\dot{\varphi}r=\omega r\), tečného zrychlení \(a_t=\ddot{\varphi}r=\alpha r\), normálového zrychlení \(a_n=\dot{\varphi}^2r=\omega^2r\) a Coriolisova zrychlení \(a_c=2\dot{\varphi}\dot{r}\) při obecném pohybu bodu v rovině.